Системы обыкновенных дифференциальных уравнений

Лекция 14

Системы дифференциальных уравнений будем рассматривать в виде

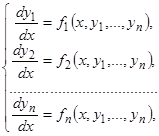(1)

называемом нормальной формой системы дифференциальных уравнений (нормальной формой Коши). Она, как вы видите, является разрешенной относительно входящих в систему производных от искомых функций. Такими системами мы и будем заниматься в дальнейшем.

Частным случаем системы является одно уравнение -го порядка, разрешенное относительно старшей производной: 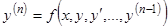. Мы с вами уже знаем, что введением новых функций 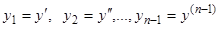оно заменится следующей системой уравнений:

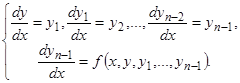(2)

Можно утверждать и обратное: вообще говоря, нормальная система уравнений первого порядка (1) эквивалентна одному уравнению порядка .

В самом деле, дифференцируем первое из уравнений (1) по : 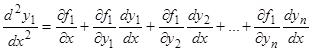; заменяем в результате 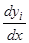их выражениями 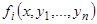, получим 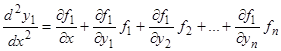, т.е. выражение вида

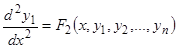(3.2)

Полученное уравнение (3.2) снова дифференцируем по ; принимая во внимание уравнения (1), получим , или

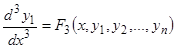. (3.3)

Продолжая этот же процесс, получим далее

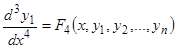, (3.4)

……………………….

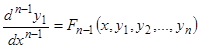, (3.n-1)

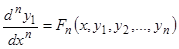. (3.n)

Составим систему 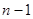уравнений из первого уравнения группы (1) и из (3.2), (3.3), …, (3.n). Обозначим ее (А). Из этой системы, вообще говоря, можно определить 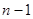величин 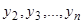через 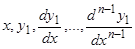. Подставляя эти выражения в (3.n), получим уравнение вида

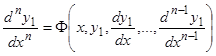, (4)

т.е. одно уравнение -го порядка. Из самого способа его получения следует, что если 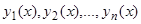являются решением системы (1), то 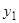удовлетворяет уравнению (4). Обратно, если мы имеем решение 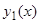уравнения (4), то, дифференцируя это решение, мы вычислим 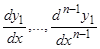. Подставим эти значения, как известные функции в систему (А); мы, по предположению, можем разрешить эту систему относительно 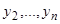, т.е. получить выражения 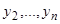как функции от . Остается показать, что функции удовлетворяют системе (1).

В самом деле, условие разрешимости системы (А) относительно 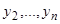состоит в том, что якобиан 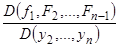отличен от нуля при рассматриваемых значениях 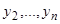. В наших предположениях 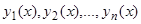обращают в тождества все уравнения системы (А); в частности, имеем тождество 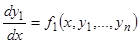. Дифференцируя это тождество по , получаем 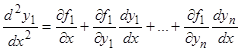, но, в силу (3.2), имеем тождественно 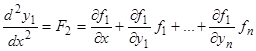. Вычитая одно тождество из другого, находим 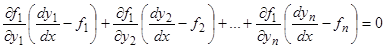. Аналогично, дифференцируя тождество (3.2) по и вычитая из полученного результата тождество (3.3), получим 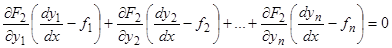и т.д., наконец . Замечая, что в силу тождества 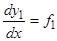, первые слагаемые всех равенств исчезают, и рассматривая оставшиеся равенства как систему 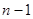уравнений с 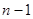неизвестными 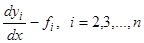, делаем вывод: так как по условию определитель системы не равен нулю, то имеют место тождества 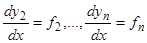, т.е. 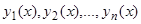действительно являются решением системы (1).

Таким образом, при сделанных допущениях интегрирование одного уравнения -го порядка (4) даёт возможность путем дифференцирований и разрешений найти решение системы (1).

Проведенное нами только что доказательство содержало предположение о разрешимости системы уравнений (А) относительно 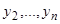. Если это условие не выполнено, то проведенные выкладки не приводят к одному уравнению -го порядка, эквивалентному системе (1). Простейший случай такого рода представляет собой система 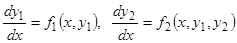. Здесь невозможно заменить систему эквивалентным ей уравнением второго порядка относительно 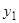. Если 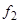действительно зависит от 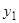, то можно вместо этого составить уравнение второго порядка относительно 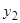, эквивалентное этой системе.

Если же второе уравнение имеет вид 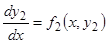, то нельзя составить и уравнение второго порядка относительно 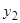, эквивалентного данной системе.

Пример. 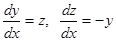. Дифференцируем первое уравнение: 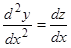; используя второе, находим 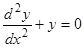, откуда 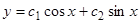. Далее, из первого уравнения .

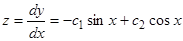В дальнейшем мы будем рассматривать системы уравнений первого порядка.

Дадим интерпретацию системы дифференциальных уравнений первого порядка, особенно важную для приложения к механике и физике. Будем обозначать независимую переменную буквой 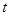и рассматривать ее как время. Искомые функции обозначим буквами 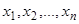, причем систему значений этих переменных будем рассматривать как координаты точки в -мерном пространстве, которое обычно называют фазовым пространством .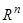

Система дифференциальных уравнений будет иметь вид

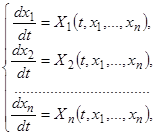(5)

Мы скажем, что система (5) определяет в каждый момент времени 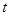в данной точке фазового пространства 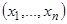компоненты скорости 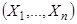движущейся точки. Можно представить всю рассматриваемую область пространства 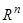заполненной непрерывной движущейся средой, причем скорости частиц этой среды в каждый момент заданы уравнениями (5).

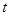Задача нахождения решения системы (5) состоит в определении величин как функций от , если дано, что при 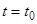координаты имеют начальные значения 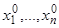. В нашей интерпретации это значит: найти функции

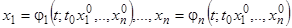, (6)

дающие для любого момента времени 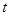положение движущейся точки, которая в начальный момент времени занимала начальное положение .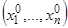

Обычно при такой интерпретации система (5) называется динамической системой, а каждое ее решение (6) — фазовой траекторией, если рассматривать его как вектор-функцию. Кривая, описываемая точкой при движении, называется траекторией движения. Уравнения траектории движения, определенного начальными значениями 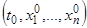, даются в параметрической форме теми же уравнениями (6), причем параметром является время .

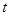Общее решение системы (5) зависит от произвольных постоянных, например от начальных значений координат 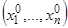при 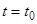, и, следовательно, определяет 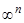траекторий.

Интерес представляет случай стационарного движения, т.е. когда функции 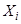не зависят явно от времени. Движение будет установившимся, и через каждую точку фазового пространства будет проходить лишь одна траектория. В случае же явной зависимости от времени функций 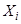, поле скоростей меняется с течением времени и фазовые траектории могут пересекаться.