Нелинейный элемент в общем случае искажает входной случайный сигнал. Принцип суперпозиции к нелинейным системам не применим. Поэтому при одновременном действии полезного регулярного сигнала и случайной помехи (рис.4.1) нелинейное преобразование этих сигналов приводит к тому, что помеха в той или иной степени может «засорить» полезный сигнал.
Пусть случайный сигнал на входе системы
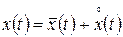 , (4.1)
, (4.1)
где 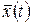 – среднее значение входа;
– среднее значение входа; 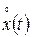 – центрированная случайная составляющая.
– центрированная случайная составляющая.

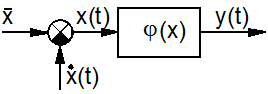
Рис. 4.1. Модель прохождения случайного сигнала через НЭ
Будем считать, что случайный процесс является стационарным и поэтому 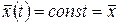 .
.
Рассмотрим выходной сигнал НЭ с характеристикой j (x). Пусть, например, это будет нелинейный безынерционный элемент с насыщением (рис. 4.2). При малом уровне помех, когда случайный сигнал x (t) (кривая 1) не выходит за пределы линейного участка с углом наклона a, для выходного сигнала можно записать
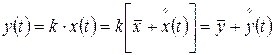 , (4.2)
, (4.2)
где 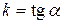 ;
; 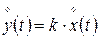 ;
; 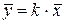 .
.
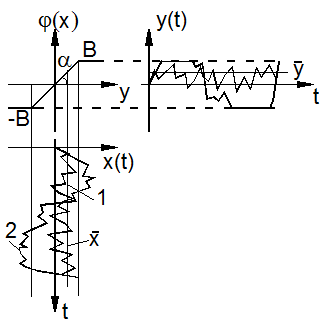
Рис. 4.2. Прохождение случайного сигнала через НЭ с насыщением
С ростом уровня помех входное воздействие выходит за пределы линейного участка (кривая 2), а среднее значение выхода 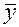 уменьшается и при очень высоком уровне помех стремиться к нулю.
уменьшается и при очень высоком уровне помех стремиться к нулю.
Таким образом, с увеличением дисперсии входного случайного сигнала, уменьшается полезный сигнал на выходе НЭ. Одновременно выходной сигнал обогащается как высокочастотными, так и низкочастотными гармониками, то есть спектральный состав сигнала на выходе перестает соответствовать спектральному составу сигнала на входе.
Рассмотрим случай прохождения случайного сигнала через НЭ с зоной насыщения, когда tg a = 1 (рис. 4.3).
В пределах линейного участка нелинейный элемент не окажет влияния на форму кривой плотности вероятности
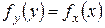 , при
, при 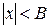 .
.
Уровень выходного сигнала не может превышать уровня насыщения. Поэтому вероятность появления сигнала 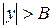 равна нулю и, следовательно,
равна нулю и, следовательно,
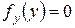 , при
, при 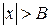 .
.
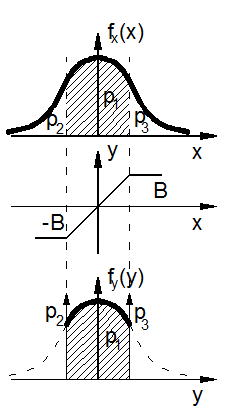
Рис. 4.3. Результат прохождения случайного сигнала
через НЭ с насыщением
Все значения сигнала x > B и x < – B будут преобразовываться в y = B или y = ‑ B, т.е. вероятность появления на выходе сигнала B и – B сильно возрастает и представляет собой d -функции, т.е. импульсы бесконечно большой величины и бесконечно малой ширины, площадь которых равна P 2 и P 3.
Можем записать
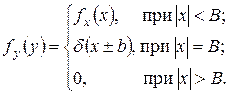
При этом 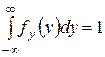 .
.
Исследование НС при действии случайных сигналов намного сложнее, чем линейных. Не существует общих точных методов их изучения и поэтому используют приближенные методы.
4.2. Постановка задачи статистической линеаризации
Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил метод статистической линеаризации. Его идея основана на приближенной замене нелинейных преобразований в системе статистически эквивалентными им линейными преобразованиями. При этом нелинейный элемент НЭ заменяется статистически эквивалентным линейным элементом ЭЛЭ. В результате система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории.
Под статистической эквивалентностью следует понимать соответствие эквивалентного элемента одному из двух критериев:
1) равенство математических ожиданий и дисперсий случайных процессов на выходе НЭ и ЭЛЭ (см. рис. 4.4)
M [ у ] = M [ u ], D [ y ] = D [ u ]; (4.3)
2) минимальное значение математического ожидания квадрата разности случайных сигналов на выходе НЭ и ЭЛЭ
 |
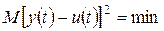 (4.4)
(4.4) Рис. 4.4. К понятию эквивалентного линейного элемента
Как уже говорилось, сигналы на входе и выходе нелинейного элемента представляют собой сумму математического ожидания (отражающего медленно меняющееся регулярное состояние) и центрированной случайной составляющей
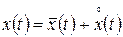 ,
,
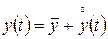 .
.
В общем случае сигнал на выходе эквивалентного линеаризованного элемента можно представить в виде
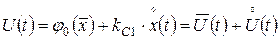 , (4.5)
, (4.5)
где 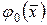 – математическое ожидание нелинейной функции j(x);
– математическое ожидание нелинейной функции j(x); 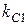 – эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.
– эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.
Таким образом, нелинейный безынерционный элемент заменяют безынерционным элементом нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (рис. 4.5).
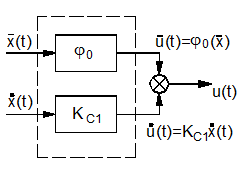 |
Рис. 4.5. Модель ЭЛЭ
Если НЭ имеет нечетную характеристику (рис. 4.6, а), функция j 0 может быть представлена в виде
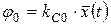 ,
,
где kC0 – эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию (по средней составляющей).
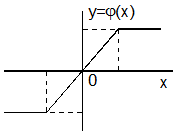 а) а) | 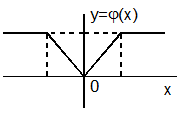 б) б) |
Рис. 4.6. Нечетная (а) и четная (б) характеристики НЭ
Коэффициенты kC 0 и kC 1 называются коэффициентами статистической линеаризации, соответственно, для математического ожидания и для центрированной случайной составляющей (см. рис. 4.7). Эти коэффициенты однозначно определяются статической характеристикой нелинейного звена и законом распределения входной величины.
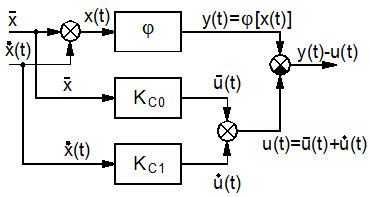
Рис. 4.7. К определению погрешности статистической линеаризации
При использовании первого критерия (4.3) для получения ЭЛЭ методом статистической линеаризации делается допущение, что сигнал на входе НЭ имеет нормальное распределение и вид этого распределения не искажается нелинейным элементом. Т. е. действительное распределение выходного сигнала заменяется нормальным с сохранением прежнего среднего значения и прежней дисперсии.
Если уравнение эквивалентного линейного звена определяется, исходя из второго критерия (4.4), то значение kC 0 совпадает со значением kC 0, полученным по первому критерию, а выражение для kC 1 получается более простым. Поэтому для получения ЭЛЭ второй критерий более предпочтителен. Погрешности же в обоих случаях получаются примерно одинаковыми по величине.
Иногда значение коэффициента статистической линеаризации kC 1 определяют путем усреднения коэффициентов, полученных по первому kC 1[1] и по второму kC 1[2] критерию.
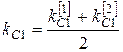 .
.
Значения коэффициентов статистической линеаризации приведены в литературе по ТАУ [2].
 2015-07-04
2015-07-04 2042
2042
