Единственным методом точного исследования динамических свойств НС, в частности их устойчивости, является метод фазовых траекторий. Однако он практически не используется для систем высокого порядка. Обычно его применение ограничено системами второго порядка.
Впервые строгую теорию устойчивости НС разработал Ляпунов [4]. Он дал точное определение устойчивости: невозмущенное движение устойчиво, если при достаточно малых начальных возмущениях вызванное ими возмущенное движение сколь угодно мало отличается от невозмущенного, при этом движение асимптотически устойчиво, если при t ® ¥ возмущенное движение стремиться к невозмущенному.
Второй (прямой) метод Ляпунова является наиболее общим методом исследования устойчивости НС. Он дает достаточные условия устойчивости. Однако его применение на практике затруднено из-за сложности определения функций Ляпунова.
В.М.Попов предложил критерий абсолютной устойчивости [2].
Под абсолютной устойчивостью понимается устойчивость нелинейной системы в целом для определенного класса нелинейностей.
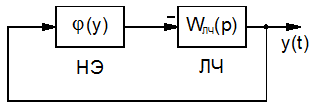
Нелинейность (см. рис.3.1, а) задается не конкретной характеристикой, а в более общем виде, например, как условие расположения статической характеристики внутри определенного угла между осью абсцисс и некоторой прямой (рис. 3.1,б).
Для определения устойчивости по этому методу используют частотную функцию вида
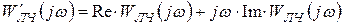 ,
,
в отличие от обычной частотной функции ЛЧ, которая, как известно, выражается как
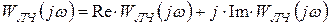 .
.
 а) а) | 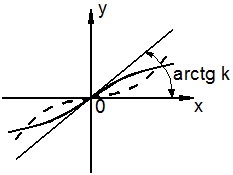 б) б) |
Рис.3.1. Способ задания характеристики НЭ внутри угла arctg k
Рассмотрим, как оценивается устойчивость НС в случаях устойчивой и неустойчивой ЛЧ системы.
· Случай 1. Линейная часть НС устойчива.
Критерий Попова для этого случая формулируется следующим образом. Система абсолютно устойчива, если через точку (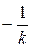 , j0) можно провести хотя бы одну прямую так, чтобы вся характеристика
, j0) можно провести хотя бы одну прямую так, чтобы вся характеристика 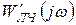 находилась от нее справа. Иллюстрация применения этого критерия приведена на рис. 3.2. Устойчивой системе соответствует рис. 3.2, а, а неустойчивой – рис. 3.2, б.
находилась от нее справа. Иллюстрация применения этого критерия приведена на рис. 3.2. Устойчивой системе соответствует рис. 3.2, а, а неустойчивой – рис. 3.2, б.
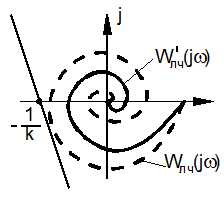 а) а) | 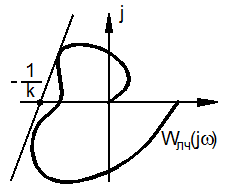 б) б) |
Рис. 3.2. Определение устойчивости НС при устойчивой ЛЧ
Этот критерий является достаточным, т.к. он дает часть области абсолютной устойчивости и его невыполнение не означает отсутствия абсолютной устойчивости.
· Случай 2. Линейная часть НС неустойчива.
Преобразуем схему НС в эквивалентную, путем введения фиктивных звеньев aф (см. рис. 3.3). В работе схемы ничего не изменилось, т.к. сигналы введенных обратных связей взаимно компенсируются.
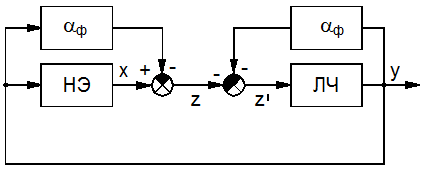
Рис. 3.3. Эквивалентная схема НС
Действительно
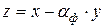 ;
; 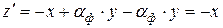 ,
,
так же, как в исходной схеме.
Для эквивалентной НС передаточная функция линейной части будет иметь вид
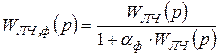 , (3.1)
, (3.1)
а характеристика нелинейного элемента -
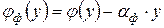 . (3.2)
. (3.2)
Пусть aф выбрано таким, что новая линейная часть с передаточной функцией (3.1) стала устойчивой, т.е. все полюса стали левыми. (Отметим, что если нельзя выбрать такое значение aф, чтобы ЛЧ стала устойчивой, то система даже при линейной зависимости j(y) любого наклона будет неустойчивой).
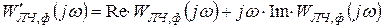 .
.
Применив к преобразованной схеме критерий Попова, получим следующее условие абсолютной устойчивости исходной схемы с неустойчивой линейной частью. Система абсолютно устойчива, если через точку (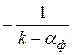 , j 0) можно провести прямую линию, проходящую слева от характеристики
, j 0) можно провести прямую линию, проходящую слева от характеристики 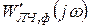 .
.
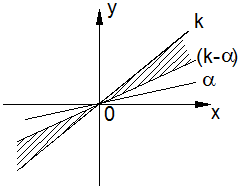
При этом характеристика НЭ jф (y) должна лежать в угле, ограниченном с одной стороны осью абсцисс. С учетом (3.2) это означает, что характеристика j (y) должна лежать вне угла (0, aф). Поэтому критерии надо дополнить требованием нахождения характеристики j (y) внутри угла (aф, k), а характеристики jф (y) – в угле [0, (k – aф)] (см. рис. 3.4, а).
Критерий Попова может быть распространен и на более общий случай нелинейности. Например, на случай, когда характеристика j (y) лежит внутри угла (k 1, k 2), где k 1 может быть как положительным, так и отрицательным (рис. 3.4, б).
 а) | 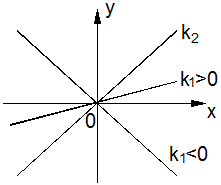 б) б) |
Рис.3.4. Определение устойчивости НС при неустойчивой ЛЧ
 2015-07-04
2015-07-04 1157
1157
