Запишем соотношения:
W(jω) = U(ω) + jV(ω)
W*(jω) = U(ω) + jωV(ω) (29)
U(-ω) = U(ω)
V(-ω) = -V(ω)
1.Из соотношений (29) следует, что кривая Найквиста и модифицированная частотная характеристика пересекают действительную ось в одних и тех же точках.
2.Если для данного интервала частот кривая Найквиста расположена в нижней (верхней) полуплоскости, то и модифицированная частотная характеристика также расположена в нижней (верхней) полуплоскости.
3.Если степень знаменателя W(p) больше степени числителя, то кривая Найквиста стремится к началу координат при ω→∞.
Для модифицированной частотной характеристики это свойство имеет место, только если степень знаменателя W(p) выше степени числителя на два и более. Если степень знаменателя W(p) больше степени числителя на единицу, то модифицированная частотная характеристика при ω→∞ будет стремиться не к началу координат, а к некоторой точке на мнимой оси.
4.Если W(p) содержит интегрирующее звено, то кривая Найквиста начинается (ω>0) из бесконечности. Модифицированная частотная характеристика в этом случае начинается из некоторой конечной точки комплексной плоскости.
5.Если W(p) имеет два интегрирующих звена, то W(jω) имеет параболический характер (у неё нет асимптот). Модифицированная частотная характеристика имеет горизонтальную асимптоту.
6.Если W(p) содержит консервативное звено, то кривая Найквиста и модифицированная частотная характеристика имеют разные наклонные асимптоты.
Уточним указанные свойства.
Обозначим:
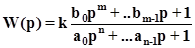

· Определим предельную точку W*(p) при ω→∞, когда n-m=1. так как мы рассматриваем только большие значения ω, то можно пренебречь всеми степенями, начиная с n-2. Следовательно, можно записать

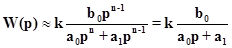
Следовательно

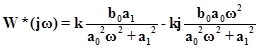
Если ω→∞, то
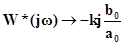
Следовательно, модифицированная частотная характеристика при n-m=1 заканчивается не в начале координат, а на мнимой оси, в точке 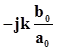 .
.
· Вычислим начальную точку(ω=0) модифицированной частотной характеристики в случае, когда W(p) содержит интегрирующее звено.
Так как мы рассматриваем малые значения ω, то можно пренебречь всеми членами в выражении W(p), имеющими степень больше единицы.
При ω→0 можно записать:

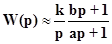
(Индексы при коэффициентах опущены)

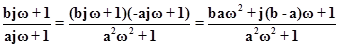
Пренебрегая 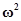 , получим
, получим
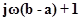
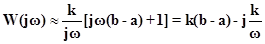
Следовательно,
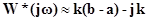
Таким образом, модифицированная частотная характеристика при ω=0 начинается из точки комплексной плоскости (k(b-a);k).
Два вышеприведённых свойства можно проиллюстрировать на примере передаточной функции

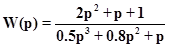
На рисунке 16 сплошной линией показана кривая Найквиста, а сплошной линией модифицированная частотная характеристика.
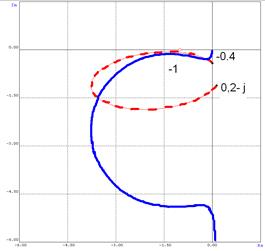
Рис. 16
· Если W(p) содержит два интегрирующих звена, то при значениях переменной p, близких к нулю, можно приближённо записать
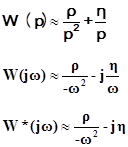 ( η>0 и ρ>0 )
( η>0 и ρ>0 )
Следовательно, модифицированная частотная характеристика будет иметь горизонтальную асимптоту - 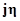 .
.
· Если W(p) содержит консервативное звено, то в окрестности точки разрыва можно приближённо записать:

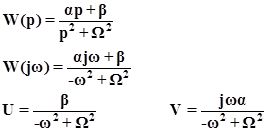
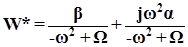
Тангенс угла наклона асимптоты кривой Найквиста:
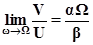
Тангенс угла наклона асимптоты модифицированной частотной характеристики:
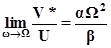
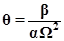

Ниже приведены примеры сравнения кривых Найквиста и модифицированных частотных характеристик (показаны пунктиром).
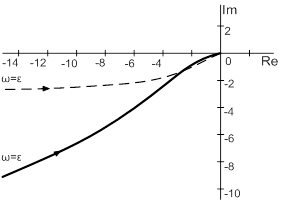 W(p) =
W(p) = 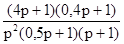 Рис. 17.
Рис. 17.
|
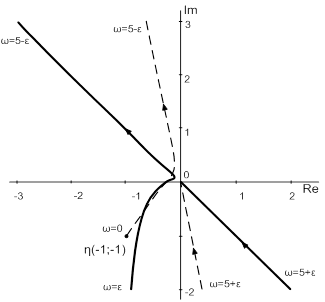 W(p) =
W(p) = 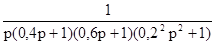 Рис. 18.
Рис. 18.
|
 2015-07-04
2015-07-04 455
455








