Параллельное соединение резистора, катушки индуктивности и конденсатора.
Резонанс токов
Цель работы – изучение основных соотношений в разветвленной цепи переменного тока, а также исследование резонанса токов.
На рис 13 изображена разветвленная цепь переменного тока, состоящая из трёх параллельно включенных приемников: резистора (лампового или проволочного реостата) с сопротивлением 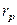 , катушки индуктивности с индуктивным сопротивлением
, катушки индуктивности с индуктивным сопротивлением 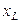 и активным сопротивлением
и активным сопротивлением 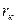 , и конденсатора с емкостным сопротивлением
, и конденсатора с емкостным сопротивлением 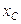 .
.
При параллельном соединении приемники электрической энергии удобнее характеризовать проводимостями, тогда от цепи, изображенной на рис. 13, можно перейти к эквивалентной ей цепи, представленной на рис. 14.
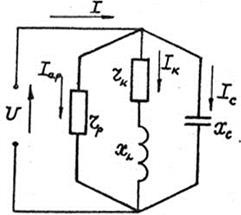 Рис.13 Рис.13 | 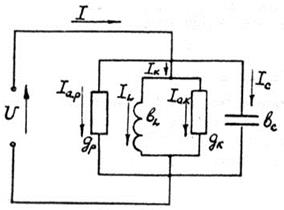 Рис.14 Рис.14 |
Здесь 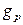 – активная проводимость резистора;
– активная проводимость резистора; 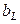 и
и 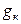 – соответственно индуктивная и активная проводимости катушки;
– соответственно индуктивная и активная проводимости катушки; 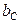 – емкостная проводимость конденсатора.
– емкостная проводимость конденсатора.
Воспользуемся известными формулами перехода от сопротивлений (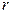 ,
, 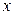 ,
, 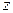 ) последовательной схемы к проводимостям (
) последовательной схемы к проводимостям (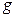 ,
, 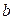 ,
, 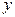 ) эквивалентной параллельной схемы:
) эквивалентной параллельной схемы:
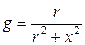 ;
; 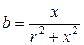 ;
; 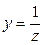 .
.
Активная проводимость резистора
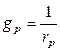 .
.
Активная проводимость катушки индуктивности
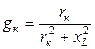 .
.
Индуктивная проводимость катушки
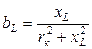 .
.
Емкостная проводимость конденсатора
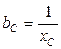 .
.
В схеме рис. 14 можно рассмотреть три случая.
1-й случай. В цепи преобладает индуктивная проводимость (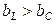 ), тогда
), тогда 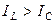 . Векторная диаграмма токов для этого случая построена на рис. 15. Активный ток резистора
. Векторная диаграмма токов для этого случая построена на рис. 15. Активный ток резистора 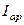 и активный ток катушки
и активный ток катушки 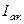 совпадают с вектором напряжения цепи
совпадают с вектором напряжения цепи 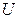 .
.
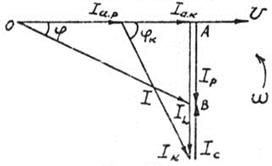
Рис.15
Индуктивный ток катушки 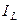 отстаёт от напряжения на угол
отстаёт от напряжения на угол 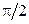 . Полный ток катушки
. Полный ток катушки 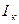 равен геометрической сумме активного и индуктивного токов катушки
равен геометрической сумме активного и индуктивного токов катушки 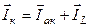 и отстает по фазе от напряжения на угол
и отстает по фазе от напряжения на угол 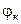 . Емкостной ток конденсатора
. Емкостной ток конденсатора 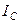 , проведенный из конца вектора
, проведенный из конца вектора 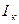 , опережает напряжение на зажимах цепи на угол
, опережает напряжение на зажимах цепи на угол 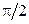 . Замыкающий вектор
. Замыкающий вектор 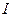 равен току в неразветвлённой части цепи.
равен току в неразветвлённой части цепи.
Из векторной диаграммы видно, что при параллельном соединении приемников активные токи складываются арифметически:
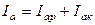 ;
;
реактивные токи – алгебраически:
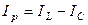 ;
;
полные токи – геометрически:
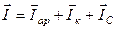 .
.
Последняя формула выражает первый закон Кирхгофа для действующих значений переменного тока.
Для практических расчетов удобно пользоваться формулой
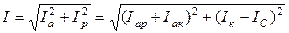 ,
,
полученной из треугольника токов ОАB (рис. 15).
2-й случай. В цепи преобладает емкостная проводимость (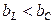 ) тогда
) тогда 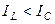 . Полный ток в цепи графически определяется аналогично первому случаю (рис. 16). Как видно из рис. 16, ток
. Полный ток в цепи графически определяется аналогично первому случаю (рис. 16). Как видно из рис. 16, ток 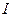 опережает напряжение
опережает напряжение 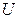 на угол
на угол 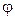 .
.
З-й случай. Равенство реактивных проводимостей (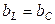 ), тогда
), тогда 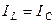 . Полный ток в этом случае (рис. 17) совпадает по фазе с напряжением (
. Полный ток в этом случае (рис. 17) совпадает по фазе с напряжением (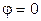 ). Этот режим называется резонансом токов, так как токи
). Этот режим называется резонансом токов, так как токи 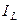 и
и 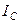 равны между собой и противоположны по фазе. Для рассматриваемой цепи (см. рис.14) условие резонанса токов может быть записано в такой форме:
равны между собой и противоположны по фазе. Для рассматриваемой цепи (см. рис.14) условие резонанса токов может быть записано в такой форме:
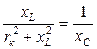 ;
;
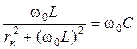 .
.
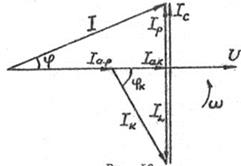 Рис.16 Рис.16 | 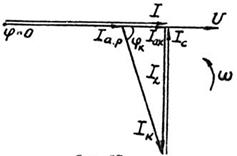 Рис.17 Рис.17 |
Очевидно, что резонанс токов, может быть достигнут изменением одного из параметров цепи: индуктивности 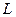 или емкости
или емкости 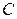 , а также изменением частоты питающей сети
, а также изменением частоты питающей сети 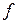 .
.
В лабораторной работе изменение режима цепи и получение резонанса токов проводится ступенчатым изменением емкости при 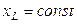 и
и 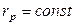 . Явление резонанса токов характеризуется следующими свойствами:
. Явление резонанса токов характеризуется следующими свойствами:
1) 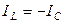 . Если катушка и конденсатор идеальные, то ток в цепи конденсатора будет равен току в цепи катушки. Практически же в момент резонанса ток в катушке
. Если катушка и конденсатор идеальные, то ток в цепи конденсатора будет равен току в цепи катушки. Практически же в момент резонанса ток в катушке 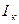 всегда больше, чем ток конденсатора
всегда больше, чем ток конденсатора 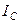 .
.
2) 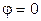 , поэтому
, поэтому 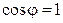 . Полная мощность всей цепи равна активной (
. Полная мощность всей цепи равна активной (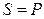 ). Следовательно, в режиме резонанса токов цепь ведет себя как активная. Причем до резонанса цепь носит активно-индуктивный характер, а после резонанса – активно-емкостной;
). Следовательно, в режиме резонанса токов цепь ведет себя как активная. Причем до резонанса цепь носит активно-индуктивный характер, а после резонанса – активно-емкостной;
3) при неизменном напряжении на зажимах цепи имеет место минимум тока в в неразветвленной части цепи (рис. 18). Действительно, ток 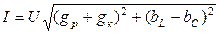 , при
, при 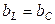 имеем
имеем 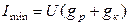 ;
;
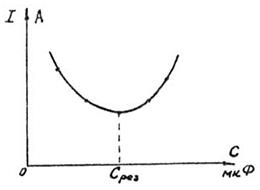
Рис. 18
4) при расчете резонансных контуров следует учитывать, что если 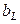 и
и 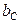 >>
>> 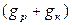 , то токи
, то токи 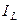 и
и 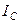 могут во много раз превышать общий ток в неразветвленной части цепи.
могут во много раз превышать общий ток в неразветвленной части цепи.
Физическая сущность резонанса токов делается ясной при рассмотрении энергетической стороны процесса. При резонансе энергия, запасенная в магнитном поле катушки, равна энергии, запасенной в электрическом поле конденсатора. При этом колебания энергии катушки и конденсатора противоположны по фазе, т.е. между катушкой и конденсатором происходит обмен энергиями. Обмена энергий между генератором, с одной стороны, и катушкой и конденсатором, с другой, – нет, и генератор передает энергию лишь в активное сопротивление. Таким образом, физическая сущность резонанса токов аналогична резонансу напряжений. Взаимный обмен реактивной энергии между катушкой индуктивности и конденсатором используется на практике, в частности для повышения коэффициента мощности на входных зажимах приемников электрической энергии.
Коэффициент мощности (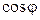 ) приемников электрической энергии
) приемников электрической энергии
Обычно электрические приемники (двигатели, трансформаторы) носят активно-индуктивный характер и работают с углом сдвига фаз 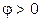 . Генератор, питающий такой приемник, линия передачи к нему и сам приемник рассчитываются на полную мощность
. Генератор, питающий такой приемник, линия передачи к нему и сам приемник рассчитываются на полную мощность 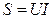 . Средняя (или активная) мощность приемника, соответствующая преобразованию электрической энергии в тепло или механическую работу, соответствует равенству
. Средняя (или активная) мощность приемника, соответствующая преобразованию электрической энергии в тепло или механическую работу, соответствует равенству 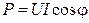 . Здесь
. Здесь 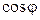 – коэффициент мощности приемника;
– коэффициент мощности приемника; 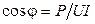 – т.е. коэффициент мощности – это отношение активной мощности к полной. Как правило,
– т.е. коэффициент мощности – это отношение активной мощности к полной. Как правило, 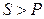 , т.е. расчетная (полная) мощность генератора и линии передачи используются не с полной эффективностью. Отсюда ясна важность для народного хозяйства повышения коэффициента мощности (в предельном случае до
, т.е. расчетная (полная) мощность генератора и линии передачи используются не с полной эффективностью. Отсюда ясна важность для народного хозяйства повышения коэффициента мощности (в предельном случае до 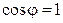 ).
).
Ток, потребляемый приемником от генератора, также зависит от коэффициента мощности, т.е.
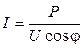 .
.
Если приемник работает при постоянной мощности 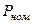 и напряжении
и напряжении 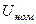 , соответствующих
, соответствующих
номинальным (паспортным) данным приемника, то ток 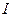 будет тем больше, чем ниже
будет тем больше, чем ниже 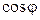 . Увеличение тока
. Увеличение тока 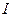 приводит к увеличению потерь энергии в генераторах, линиях передачи и приемниках. Таким образом, для полного использования расчетной мощности генераторов и уменьшения потерь энергии необходимо повышать
приводит к увеличению потерь энергии в генераторах, линиях передачи и приемниках. Таким образом, для полного использования расчетной мощности генераторов и уменьшения потерь энергии необходимо повышать 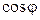 приемников. С целью повышения коэффициента мощности к приемнику подключают параллельно батарею конденсаторов.
приемников. С целью повышения коэффициента мощности к приемнику подключают параллельно батарею конденсаторов.
В этом случае 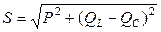 , где
, где 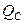 – емкостная мощность конденсаторов;
– емкостная мощность конденсаторов; 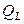 – индуктивная мощность приемника.
– индуктивная мощность приемника.
При резонансе токов 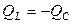 ,
, 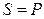 ,
, 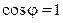 . Обычно коэффициент мощности приемников повышают до значения
. Обычно коэффициент мощности приемников повышают до значения 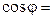 0,92-0,95, так как дальнейший его рост требует значительного увеличения емкости батареи конденсаторов, а следовательно, увеличения ее стоимости. Емкость конденсатора, который необходимо подключить параллельно приемнику для повышения коэффициента мощности с величины
0,92-0,95, так как дальнейший его рост требует значительного увеличения емкости батареи конденсаторов, а следовательно, увеличения ее стоимости. Емкость конденсатора, который необходимо подключить параллельно приемнику для повышения коэффициента мощности с величины 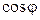 до величин!
до величин! 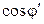 , может быть определена по формуле
, может быть определена по формуле
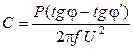 ,
,
где 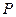 – активная мощность приемника;
– активная мощность приемника; 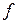 – частота сети,
– частота сети, 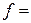 50 Гц;
50 Гц; 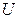 – напряжение сети.
– напряжение сети.
Программа работы
1. Исследовать работу схемы, включая поочередно резистор, катушку и конденсатор.
2. Исследовать работу параллельно включенных резистора, катушки и конденсатора при переменной емкости до резонанса токов, при резонансе и после резонанса.
3. Рассчитать величину емкости, необходимую для повышения коэффициента мощности приемника, состоящего из параллельно включённых резистора и катушки индуктивности, до наибольшего значения 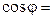 1 и сравнить с данными опыта (строка 6 в табл. 3)*.
1 и сравнить с данными опыта (строка 6 в табл. 3)*.
1. Собирается схема (рис. 19). Автотрансформатором AT устанавливается напряжение в пределах 90... 120 В, которое поддерживается постоянным при всех измерениях.
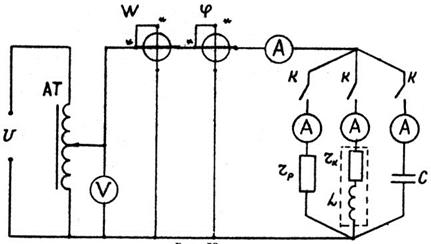
Рис.19
2. Для выполнения первой части работы поочередно включаются резистор, катушка и конденсатор. В каждом случае показания приборов записываются в таблицу наблюдений.
3. Вторая часть работы выполняется при одновременном включении всех трех приемников. Исследование ведется следующим образом. Изменяя емкость батареи конденсаторов, цепь настраивают по фазометру (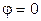 ) в резонансное состояние. Некоторая доводка до резонансного состояния возможна изменением положения сердечника в катушке. После этого сердечник заклинивают, чтобы
) в резонансное состояние. Некоторая доводка до резонансного состояния возможна изменением положения сердечника в катушке. После этого сердечник заклинивают, чтобы 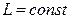 . Далее, изменяя емкость от 0 до максимально возможного значения, снимают показания приборов двух опытов до резонанса токов и двух – после резонанса. Результаты опытов заносят в табл. 3.
. Далее, изменяя емкость от 0 до максимально возможного значения, снимают показания приборов двух опытов до резонанса токов и двух – после резонанса. Результаты опытов заносят в табл. 3.
Таблица 3
| Состояние схемы | Измеряются | Вычисляются | ||||||||||||
| С, мкФ | U В | I, А | Iap, А | Iк, А | Iс, А | φ, град | P, Вт | P, Вт | Q, ВАр | Qс, ВАр | QL, ВАр | S, ВА | ||
| I.часть 1. Включается резистор | ||||||||||||||
| 2. Включается катушка | ||||||||||||||
| 3. Включается конденсатор | ||||||||||||||
| II.часть 4. C=0 | ||||||||||||||
| 5. C<Cрез | ||||||||||||||
| 6. Резонанс токов С= Cрез | ||||||||||||||
| 7. С>Cрез | ||||||||||||||
| 8. С= Cmax | ||||||||||||||
Содержание отчёта
1. Программа работы.
2. Схема соединений (рис. 19).
3. Таблица вычислений и наблюдений (табл. 3).
4. Векторные диаграммы токов для всех строк таблицы, кроме седьмой.
5. Треугольники мощностей для пятой, шестой и восьмом строк таблицы.
6. Кривая тока 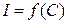 по данным строк 4...8 табл. 3.
по данным строк 4...8 табл. 3.
7. Выводы по работе.
При построении векторных диаграмм токов для строк 4...8 табл. 3 рекомендуется вначале задаться вектором напряжения 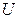 (см. рис. 15). С вектором напряжения
(см. рис. 15). С вектором напряжения 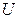 совпадает по фазе ток в резисторе
совпадает по фазе ток в резисторе 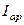 . Из конца вектора
. Из конца вектора 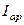 под углом
под углом 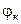 (значение угла
(значение угла 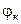 берется из табл. 3, строка 2) проводится вектор тока
берется из табл. 3, строка 2) проводится вектор тока 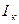 .
.
*Пункт 3 выполняется в порядке УИРС.
Вектор тока 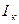 раскладывается графически на два вектора
раскладывается графически на два вектора 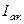 и
и 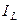 . Эта часть диаграммы будет одинаковой для всех строк, начиная с четвертой. Из конца вектора
. Эта часть диаграммы будет одинаковой для всех строк, начиная с четвертой. Из конца вектора 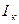 проводится вектор
проводится вектор 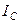 . Замыкающий вектор
. Замыкающий вектор 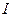 представляет собой ток в неразветвленной части цепи.
представляет собой ток в неразветвленной части цепи.
Треугольник мощностей (рис. 20) строится подобно векторной диаграмме токов, причем мощности предварительно вычисляют по следующим формулам:
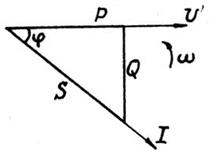 Рис. 20 Рис. 20 | полная мощность всей цепи 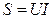 ; активная мощность всей цепи ; активная мощность всей цепи 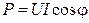 ; реактивная мощность всей цепи ; реактивная мощность всей цепи 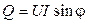 емкостная мощность конденсатора емкостная мощность конденсатора 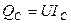 ; индуктивная мощность катушки ; индуктивная мощность катушки 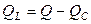 . . |
 2015-07-04
2015-07-04 3117
3117