Резонансом называется такой режим работы цепи, содержащей индуктивные и емкостные элементы, при котором ее полное входное сопротивление (или проводимость) является вещественной величиной и, как следствие, ток и напряжение на входе совпадают по фазе.
1) цепь с последовательным соединением (резонанс напряжений)
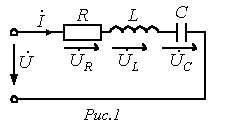
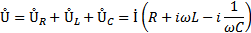 ;
;
где полное комплексное сопротивление:
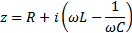 ;
;
или в показательной форме: 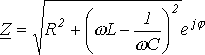 ;
;
где фаза: 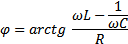 ; реактивная составляющая:
; реактивная составляющая: 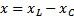 .
.
В зависимости от соотношения между 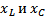 возможны три варианта (при нулевой начальной фазе тока):
возможны три варианта (при нулевой начальной фазе тока):
1.  или
или 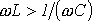 и, следовательно,
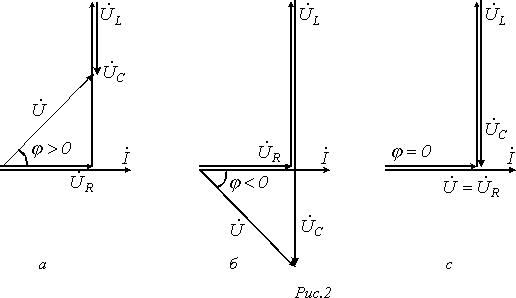
и, следовательно, 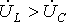 : в цепи будет преобладать индуктивность (цепь будет носить индуктивный характер); напряжение будет опережать ток и сдвиг фаз будет положительным:
: в цепи будет преобладать индуктивность (цепь будет носить индуктивный характер); напряжение будет опережать ток и сдвиг фаз будет положительным: 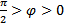 . Векторная диаграмма для этого случая представлена на рис. 2,а.
. Векторная диаграмма для этого случая представлена на рис. 2,а.
2. В цепи преобладает емкость, т.е. 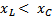
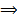 -π/2 < φ < 0 и
-π/2 < φ < 0 и 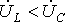 – напряжение отстает от тока и цепь будет носить емкостной характер (векторная диаграмма – рис. 2,б).
– напряжение отстает от тока и цепь будет носить емкостной характер (векторная диаграмма – рис. 2,б).
3. 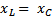 ;
; 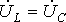 ;
; 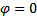 - случай резонанса напряжений (рис. 2,с) – напряжение совпадает по фазе с током, цепь будет носить резистивный характер. При этом Z=R – условие получения резонанса, т.е. полное комплексное сопротивление (проводимость) должны быть вещественными.
- случай резонанса напряжений (рис. 2,с) – напряжение совпадает по фазе с током, цепь будет носить резистивный характер. При этом Z=R – условие получения резонанса, т.е. полное комплексное сопротивление (проводимость) должны быть вещественными.
В этом случае в цепи будет протекать максимальный ток 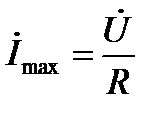 . Он создаёт на реактивных элементах одинаковые по величине и противоположные по направлению напряжения:
. Он создаёт на реактивных элементах одинаковые по величине и противоположные по направлению напряжения: 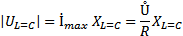 , которые могут в
, которые могут в 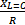 раз превышать напряжение источника воздействия.
раз превышать напряжение источника воздействия.
Резонансную частоту можно найти из формулы условия резонанса напряжений:
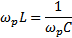
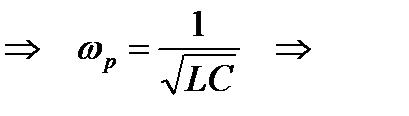
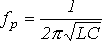 .
.
Таким образом, при резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В предельном случае при 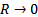 он стремится к бесконечности
он стремится к бесконечности 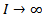 , и соответственно этому в
, и соответственно этому в 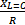 раз по сравнению с напряжением источника питания будут увеличиваться напряжения на катушке и конденсаторе.
раз по сравнению с напряжением источника питания будут увеличиваться напряжения на катушке и конденсаторе.
Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки и электрическим полем конденсатора, причем сумма энергий полей остаётся постоянной. То же справедливо, если в цепи имеется несколько индуктивных и ёмкостных элементов, тогда вводят понятие эквивалентных величин, которые соответственно определяются:
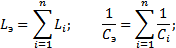
Резонансными кривыми называются зависимости тока и напряжения от частоты. Одной из основных характеристик резонансного контура является добротность, определяемая как отношение напряжения на реактивном элементе к входному напряжению (или отношение реактивного и резистивного сопротивления):
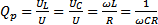 .
.
Она является безразмерной величиной и характеризует частотно-избирательные свойства резонансного контура, в частности, его полосу пропускания 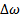 :
: 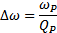 .
.
Другим параметром резонансного контура является характеристическое сопротивление:
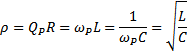 .
.
2) Цепь с параллельным соединением (резонанс токов)
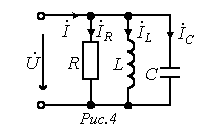 Для этой цепи:
Для этой цепи: 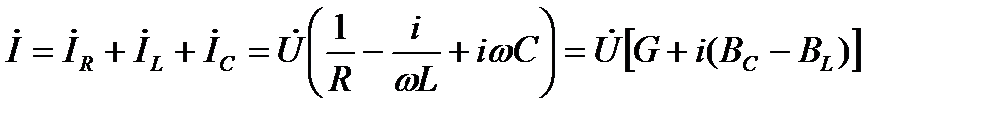 , тогда полная комплексная проводимость:
, тогда полная комплексная проводимость: 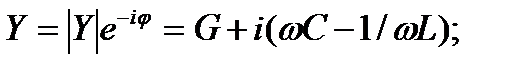
где ее модуль: 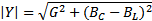 ; фаза:
; фаза: 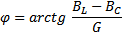 .
.
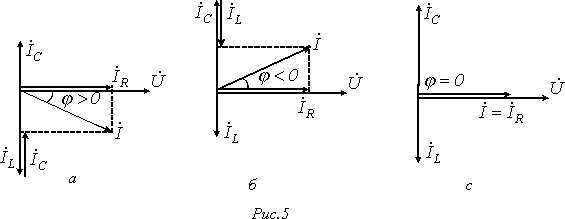
В зависимости от соотношения проводимостей реактивных элементов возможны три следующих случая:
1.  ; следовательно,
; следовательно, 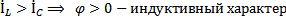 цепи (напряжение опережает) (векторная диаграмма на рис. 5,а).
цепи (напряжение опережает) (векторная диаграмма на рис. 5,а).
2. 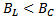 ; следовательно,
; следовательно, 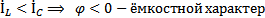 цепи (ток опережает) (рис. 5,б).
цепи (ток опережает) (рис. 5,б).
3. 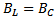 →
→ 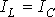 - условие резонанса токов, при котором полная комплексная проводимость является вещественной:
- условие резонанса токов, при котором полная комплексная проводимость является вещественной: 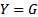 и сдвиг фаз между током и напряжением равен нулю:
и сдвиг фаз между током и напряжением равен нулю: 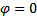 (рис. 5,с). При этом
(рис. 5,с). При этом 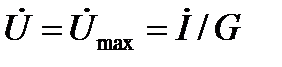 .
.
Таким образом, при резонансе токов в реактивных элементах возникают равные по величине и противоположные по направлению (знаку) токи: 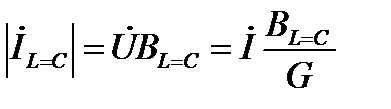 , которые могут превышать общий входной ток в
, которые могут превышать общий входной ток в 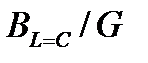 раз.
раз.
Из условий резонанса напряжений и токов видно, что в обоих этих случаях резонансная частота определяется одинаково. Однако это справедливо только для простейших схем с последовательным или параллельным соединением. В общем случае, при определении резонансной частоты в цепи произвольной конфигурации, необходимо исходить из условия вещественности функции входного сопротивления (проводимости) цепи. Так, для приведенного примера полная комплексная проводимость определится:
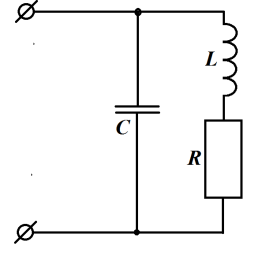
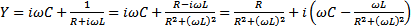 .
.
Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то условие резонанса будет иметь вид: 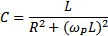 , откуда можно непосредственно определить значение резонансной частоты данного контура.
, откуда можно непосредственно определить значение резонансной частоты данного контура.
При определении резонансной частоты в сложных схемах со смешанным соединением аналитические выражения для входной реактивной проводимости 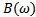 или сопротивления
или сопротивления 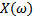 необходимо представить в виде отношения двух полиномов по степени частоты
необходимо представить в виде отношения двух полиномов по степени частоты 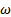 :
: 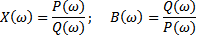 . Тогда корни уравнения
. Тогда корни уравнения 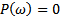 дадут значения частот, соответствующих резонансам напряжений; а корни уравнения
дадут значения частот, соответствующих резонансам напряжений; а корни уравнения 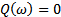 - частоты для резонансов токов. При этом общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме после ее приведения (при помощи эквивалентных преобразований) к минимальному количеству этих элементов и режимы резонансов токов и напряжений чередуются по частоте.
- частоты для резонансов токов. При этом общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме после ее приведения (при помощи эквивалентных преобразований) к минимальному количеству этих элементов и режимы резонансов токов и напряжений чередуются по частоте.
 2015-04-23
2015-04-23 776
776








