Основные свойства определителей

1º. Если каждый элемент какой-либо строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в первом из которых в этой строке записано первое слагаемое, во втором – второе, а все остальные строки (столбцы) этих двух определителей совпадают с соответствующими строками (столбцами) исходного определителя.

►Доказательство проводим для строк. Применяя разложение по i -й строке, получаем:

=

= + = =

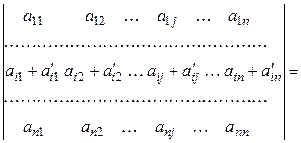
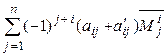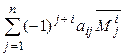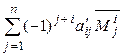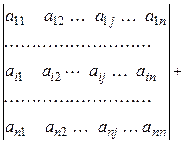
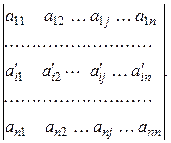
(здесь следует учесть, что во всех трех определителях алгебраические дополнения к соответствующим элементам i -й строки совпадают). ◄

2º. Если в определителе все элементы какой-либо строки (столбца) умножить на число, то определитель умножится на это число (общий множитель строки или столбца можно выносить за знак определителя).

►Доказательство снова проводим для строк. Разлагаем определитель по i -й строке:

. ◄

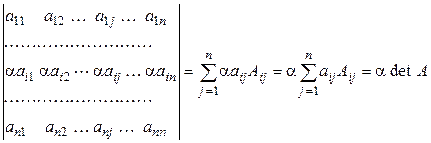Первое и второе свойства носят название линейности определителя.

3º. Если определитель содержит строку или столбец, полностью состоящий из нулей, то он равен нулю.

Доказательство вытекает из 2-го свойства.

4º. Если определитель содержит две одинаковые строки (столбца), то он равен нулю.

►Доказательство вытекает из леммы 1.5: если две одинаковые строки поменять местами, то, с одной стороны, определитель не изменится, с другой стороны, он поменяет знак.◄

5º. Если определитель содержит две пропорциональные строки (столбца), то он равен нулю.

Доказательство вытекает из второго и четвертого свойств.

6º (основное свойство определителей). Если к какой-либо строке (столбцу) определителя прибавить другую его строку (столбец), умноженную на число, то определитель при этом не изменится.

►Прибавим к i -й строке определителя k -ю строку, умноженную на 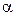. На основании 1-го свойства имеем:

=

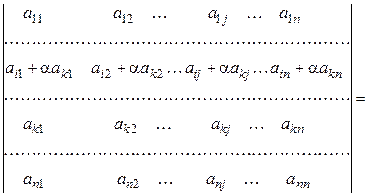
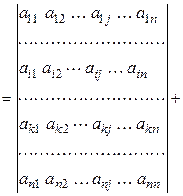
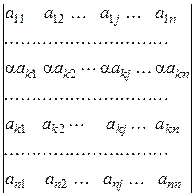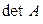
(так как второй определитель обращается в 0 на основании 5-го свойства).◄

Следствие. Если к какой-либо строке (столбцу) определителя прибавить линейную комбинацию других его строк (столбцов), то определитель при этом не изменится.

7º. Определитель матрицы, комплексно сопряженной данной, равен числу, комплексно сопряженному ее определителю.

Доказательство легко проводится методом математической индукции, используя разложение, например, по первой строке.

8º. Определитель произведения матриц равен произведению их определителей, т. е. .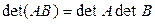

►Для простоты доказательство проведем для квадратных матриц второго порядка (для матриц n -го порядка оно точно такое же). Пусть

.

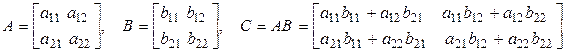Обозначим

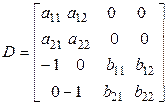
квадратную матрицу четвертого порядка и преобразуем ее следующим образом: прибавим к первой строке третью, умноженную на 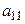, и четвертую, умноженную на 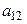, а ко второй – третью, умноженную на 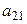, а четвертую – на 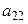. Получим матрицу

.

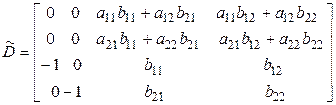Заметим, что в ее правом верхнем углу получилась именно матрица 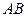. Вычислим определители матриц 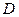и 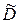по теореме Лапласа, в обоих случаях выделяя первые две строки:

, .

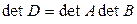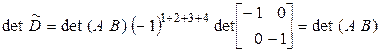На основании 6-го свойства и следствия к нему определители матриц 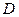и 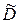совпадают, откуда и вытекает доказываемое утверждение. ◄

Теорема 1.3 (аннулирования). Сумма произведений какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.

►Доказательство опять проводим для строк. Наряду с исходным определителем

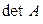
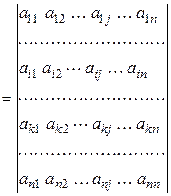
рассмотрим определитель, имеющий две одинаковые строки (i -ю и k -ю) и вычислим его разложением по k -й строке. Конечно же, он равен нулю, и поэтому

.◄

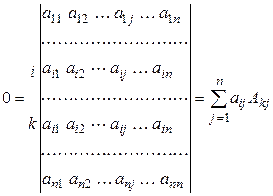Замечание. Утверждения теорем 1.1 и 1.3 можно записать одной формулой:

.

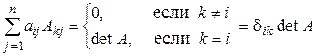Теорема 1.4 (замещения). Пусть заданы определитель n -го порядка 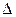и упорядоченный набор чисел

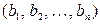. (1.13)

Сумма произведений чисел (1.13) на алгебраические дополнения соответствующих элементов какого-либо столбца (строки) определителя равна определителю, полученному из 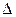заменой этого столбца (строки) на столбец 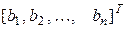(строку ).

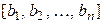►На этот раз доказательство проведем для столбцов. Обозначим 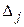– определитель, полученный из 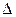заменой 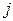-го столбца на столбец 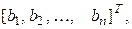и вычислим этот определитель разложением по j -му столбцу:

.◄

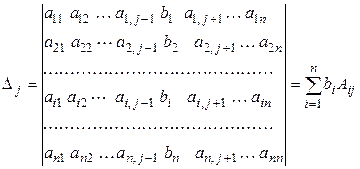Пример. ▼ Вычислим определитель с использованием основного свойства. Стрелками обозначим проводимые действия. Так, например, если ко второй строке прибавляем четвертую, умноженную на (–1), то стрелка идет в направлении от четвертой строки ко второй, и рядом с ней написана (–1). Цель преобразований состоит в том, чтобы получить в какой-либо строке (или столбце) все нули, за исключением разве что одного элемента.

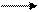
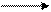
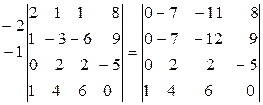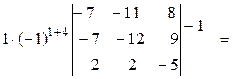
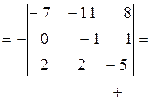
= [понижаем порядок определителя, разлагая его по первому столбцу] = 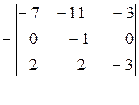= [разлагаем по второй строке] =

.▲

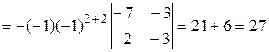В заключение параграфа сформулируем

Определение. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.