2015-07-21
1766
Идея метода заключается в делении отрезка, на котором содержится корень, пополам, до тех пор, пока не будет достигнута заданная точность.
Поделим отрезок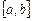 
пополам. Координата середины отрезка определится как 
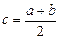. Теперь корень остался на одной из частей: 
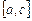или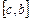 
. Если 
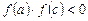, то это говорит о том, что функция на отрезке 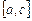меняет свой знак, то есть на данном интервале находится корень. В этом случае деление отрезка можно повторить, приняв в качестве нового правого конца точку 
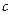, т.е. приравняв 
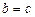. В противном случае, корень попал на половину 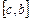, и необходимо изменить значение левого конца отрезка: 
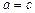. Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности: 
.
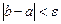ПРИМЕР 1.2. Найдем первый корень уравнения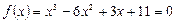 
с точностью 
.
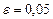Вычисления выполним при помощи электронной таблицы Excel, задавая начальные значения концов интервала изоляции и формул для выполнения итераций. Результаты оформляются в виде таблицы
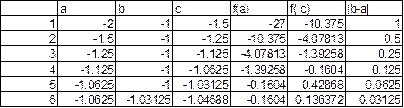
где во второй строке во втором и третьем столбцах заданы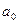 
, 
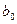– начальные границы интервала изоляции корня; 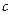вычисляется по формуле 
, 
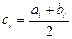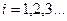, а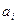 
, 
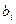в свою очередь определяются как
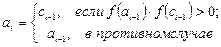и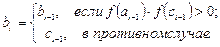 
В результате расчета приближенное значение первого корня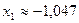 
при заданной величине точности 
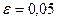. При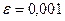 
необходимо сделать большее число итераций, поэтому к приведенной выше таблице добавятся строки:
Как можно видеть, значение корня в этом случае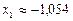 
, что является более близким к точному значению. Второй и третий корни находятся аналогично.
