Для метода простой итерации (МПИ) уравнение (1.1) необходимо сначала преобразовать к виду 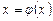 . Это всегда можно сделать с помощью эквивалентных преобразований. Далее, выберем начальное приближение
. Это всегда можно сделать с помощью эквивалентных преобразований. Далее, выберем начальное приближение 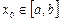 . Следующие итерации производятся по формуле:
. Следующие итерации производятся по формуле: 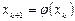 , т.е.
, т.е. 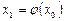 ,
, 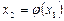 , и т.д. Если последовательность
, и т.д. Если последовательность 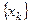 ,
, 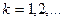 сходится, то
сходится, то 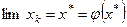 , то есть в пределе получаем искомое решение уравнения. Итерационный процесс следует остановить, когда
, то есть в пределе получаем искомое решение уравнения. Итерационный процесс следует остановить, когда 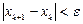 . В качестве начального приближения обычно берут середину отрезка
. В качестве начального приближения обычно берут середину отрезка 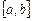 :
: 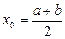 .
.
Привести исходное уравнение (1.1) к виду 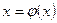 можно бесконечным числом способов. Из всевозможных функций j (x) выбирают ту, которая порождает сходящуюся к корню последовательность
можно бесконечным числом способов. Из всевозможных функций j (x) выбирают ту, которая порождает сходящуюся к корню последовательность 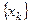 .
.
Достаточное условие сходимости. Пусть 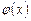 имеет производную на отрезке
имеет производную на отрезке 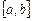 ,
, 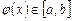 и
и 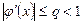 для всех
для всех 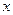 из отрезка
из отрезка 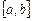 . Тогда итерационный процесс сходится к корню уравнения, т.е.
. Тогда итерационный процесс сходится к корню уравнения, т.е. 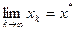 .
.
Доказательство. Из формулы МПИ следует, что
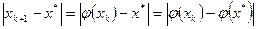
Применяя теорему Лагранжа о среднем, получим
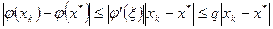 .
.
Аналогично
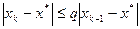 ,
, 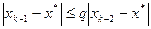 и т.д.
и т.д.
Следовательно,
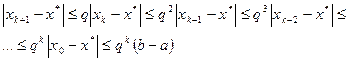
Так как 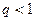 , то
, то 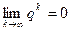 и, следовательно,
и, следовательно, 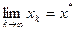 .
.
Геометрическая интерпретация метода простой итерации представлена на рис. 1.4 для случаев 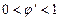 (а),
(а), 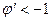 (б),
(б), 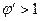 (в) и
(в) и 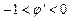 (г).
(г).
 | 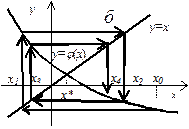 |
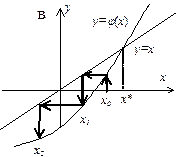 | 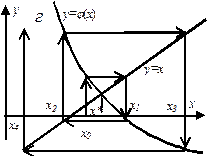 |
| Рис. 1.4.Сходящийся (а, б) и расходящийся (в, г) МПИ |
 2015-07-21
2015-07-21 746
746








