Выберем произвольное 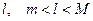 . Из определения точных граней следует, что найдутся такие значения
. Из определения точных граней следует, что найдутся такие значения 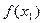 и
и 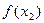 (
(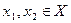 ), что
), что
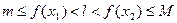
По теореме 2 существует число  , лежащее между
, лежащее между 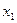 и
и 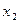 , такое, что
, такое, что 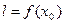 . В силу произвольности выбранного
. В силу произвольности выбранного 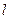 это означает, что
это означает, что 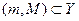 . С учетом определения чисел
. С учетом определения чисел 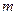 и
и 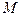 отсюда следует, что множество
отсюда следует, что множество 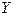 есть некоторый промежуток?
есть некоторый промежуток?
Теорема 1 (первая теорема Вейерштрасса). Всякая непрерывная на отрезке 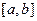 функция
функция  ограничена на этом отрезке.
ограничена на этом отрезке.
Д о к а з а т е л ь с т в о. Предположим противное. Тога для любого натурального 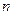 найдется такая точка
найдется такая точка 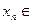
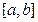 , что
, что
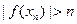 . . | (1) |
Так как последовательность 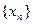 ограничена (
ограничена (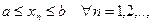 ), то по теореме Больцано-Вейерштрасса она содержит сходящуюся подпоследовательность
), то по теореме Больцано-Вейерштрасса она содержит сходящуюся подпоследовательность 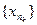 . Пусть
. Пусть
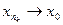 при
при 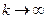 .
.
Очевидно, что 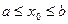 (для того, чтобы убедиться в этом достаточно в неравенствах
(для того, чтобы убедиться в этом достаточно в неравенствах 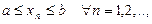 перейти к пределу при
перейти к пределу при 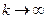 ). Поэтому в силу непрерывности функции
). Поэтому в силу непрерывности функции  на отрезке
на отрезке 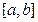
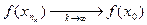
Следовательно, последовательность 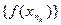 ограничена, что, противоречит тому, что согласно (1)
ограничена, что, противоречит тому, что согласно (1) 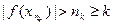
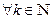 ?
?
Пусть функция  определена на множестве
определена на множестве 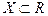 . Далее вместо символов
. Далее вместо символов 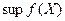 и
и 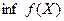 , служащих для обозначения точных верхней и нижней граней множества значений функции
, служащих для обозначения точных верхней и нижней граней множества значений функции  на множестве
на множестве 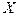 часто будем использовать символы
часто будем использовать символы
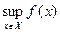 и
и 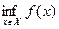 , соответственно.
, соответственно.
Теорема 2 (вторая теорема Вейерштрасса). Всякая непрерывная на отрезке 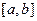 функция
функция  достигает на нем своих точных верхней и нижней граней, т.е.существуют такие точки
достигает на нем своих точных верхней и нижней граней, т.е.существуют такие точки 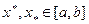 ,что
,что
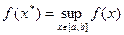 ,
, 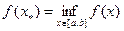 .
.
Д о к а з а т е л ь с т в о. Докажем, например, утверждение теоремы относительно точной верхней грани. Доказательство проведем от противного. А именно, положим 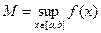 и предположим, что
и предположим, что
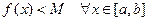 .
.
Тогда, очевидно, функция
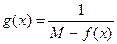
будет непрерывной на отрезке 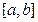 . Поэтому по теореме 1 она будет ограниченной на этом отрезке. В частности, найдется такое
. Поэтому по теореме 1 она будет ограниченной на этом отрезке. В частности, найдется такое 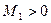 , что
, что
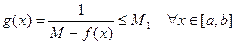
Следовательно
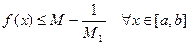 ,
,
а это противоречит тому, что 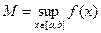 ?
?
Замечание 1. Теорема 2 по сути гласит, что во множестве значений 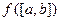 непрерывной на отрезке
непрерывной на отрезке 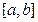 функции
функции  имеется наибольший и наименьший элементы. Они, соответственно, называются наибольшим и наименьшим значениями функции, при этом точки
имеется наибольший и наименьший элементы. Они, соответственно, называются наибольшим и наименьшим значениями функции, при этом точки 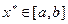 и
и 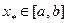 , в которых функция
, в которых функция  принимает эти значения, называются, соответственно точкой максимума и точкой минимума функции
принимает эти значения, называются, соответственно точкой максимума и точкой минимума функции  на отрезке
на отрезке 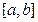 . Теорему 2, таким образом, можно рассматривать как теорему о существовании точек максимума и минимума непрерывной на отрезке функции.
. Теорему 2, таким образом, можно рассматривать как теорему о существовании точек максимума и минимума непрерывной на отрезке функции.
Наибольшее и наименьшее значения функции  на отрезке
на отрезке 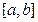 обычно обозначаются символами
обычно обозначаются символами 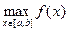 и
и 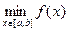
С учетом следствия из второй теоремы Больцано-Коши, из второй теоремы Вейерштрасса вытекает такое
Следствие. Множество значений непрерывной на отрезке 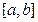 функции
функции  является отрезком
является отрезком 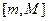 , где
, где 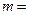
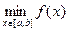 ,
, 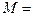
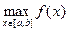 .
.
§12а. Непрерывность и разрывы монотонных функций.
n01. Точки разрыва монотонных функций.
Теорема 1 (о существовании односторонних пределов монотонной функции). Пусть функция  монотонна на интервале
монотонна на интервале 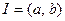
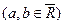 . Тогда в каждой точке
. Тогда в каждой точке 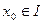 существуют конечные, односторонние пределы
существуют конечные, односторонние пределы
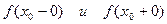 ,
,
причем
а) если функция  не убывает на интервале
не убывает на интервале 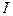 , то
, то
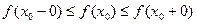 , , | (1) |
б) если же функция  не возрастает на нем, то
не возрастает на нем, то
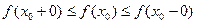 . . | (2) |
Д о к а з а т е л ь с т в о. Пусть для определенности функция  не убывает на интервале
не убывает на интервале 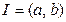 . Тогда при
. Тогда при 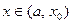 множество ее значений ограничено сверху:
множество ее значений ограничено сверху:
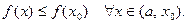
Пусть
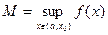 ?
?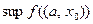
Из предыдущего неравенства следует, что
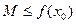 | (3) |
Так как каждую точку 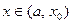 можно представить в виде
можно представить в виде
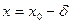
при некотором 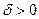 , то по определению точной верхней грани
, то по определению точной верхней грани 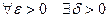 :
:
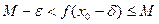 ,
,
а поскольку функция  – неубывающая, то при
– неубывающая, то при 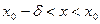 имеем
имеем
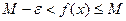 .
.
В силу произвольности 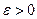 это означает, что
это означает, что 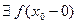 и
и 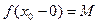 . Поэтому в силу (3)
. Поэтому в силу (3)
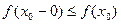 .
.
Аналогично устанавливается, что 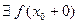 и
и
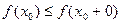 ?
?
Следствие. Если функция  – монотонна на интервале
– монотонна на интервале 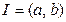 , то каждая точка
, то каждая точка 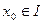 является либо точкой непрерывности функции
является либо точкой непрерывности функции  , либо точкой ее разрыва 1-го рода, и, следовательно, монотонная функция не может иметь точек разрыва 2-го рода.
, либо точкой ее разрыва 1-го рода, и, следовательно, монотонная функция не может иметь точек разрыва 2-го рода.
Теорема 2 (о мощности множества точек разрыва монотонной функции). Множество точек разрыва монотонной на интервале функции не более чем счетно.
Д о к а з а т е л ь с т в о. Для определенности пусть  – неубывающая на интервале
– неубывающая на интервале 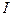 функция. Пусть
функция. Пусть 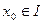 – некоторая точка разрыва функции
– некоторая точка разрыва функции  . Тогда одно из неравенств (1) строгое и, следовательно,
. Тогда одно из неравенств (1) строгое и, следовательно,
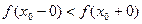
Так как между любыми двумя различными вещественными числами лежит хотя бы одно рациональное число, то отсюда следует, что найдется такое рациональное число 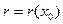 , что
, что
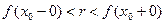 .
.
Таким образом, каждой точке разрыва может быть поставлено в соответствие некоторое рациональное число.
Если 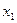 и
и 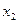
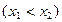 – две точки разрыва функции
– две точки разрыва функции  на интервале
на интервале 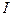 , а
, а 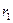 и
и 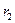 – соответствующие им рациональные числа:
– соответствующие им рациональные числа:
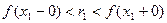 ,
,
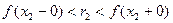 ,
,
то в силу того, что при 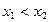 для неубывающей функции по теореме 1 будем иметь
для неубывающей функции по теореме 1 будем иметь
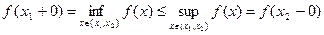
и, следовательно,
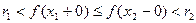 .
.
т.е. различным точкам разрыва поставлены в соответствие различные рациональные числа. Таким образом, установлено взаимно однозначное соответствие между множеством всех точек разрыва функции  и некоторым подмножеством множества рациональных чисел. А поскольку всякое подмножество множества рациональных чисел не более чем счетно, то не более чем счетно и множество точек разрыва функции
и некоторым подмножеством множества рациональных чисел. А поскольку всякое подмножество множества рациональных чисел не более чем счетно, то не более чем счетно и множество точек разрыва функции  ?
?
n02. Непрерывность монотонных функций.
Теорема 3 (критерий непрерывности монотонной функции). Для того, чтобы монотонная на отрезке 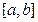 функция
функция  была непрерывной на нем, необходимо и достаточно, чтобы множество ее значений было отрезком.
была непрерывной на нем, необходимо и достаточно, чтобы множество ее значений было отрезком.
Д о к а з а т е л ь с т в о. Необходимость условия теоремы имеет место в силу следствия из второй теоремы Вейерштрасса. Поэтому нужно доказать лишь достаточность условия теоремы.
Пусть функция 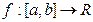 – монотонна и
– монотонна и 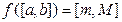 . Предположим, тем не менее, что она не является непрерывной на отрезке
. Предположим, тем не менее, что она не является непрерывной на отрезке 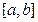 . Для определенности будем считать, что функция
. Для определенности будем считать, что функция  – неубывающая.
– неубывающая.
Пусть 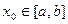 – точка разрыва функции
– точка разрыва функции  . Тогда, либо
. Тогда, либо
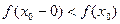 , , | (4) |
либо
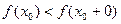 . . | (5) |
В первом из этих случаев, в силу того, что функция  – неубывающая, имеем
– неубывающая, имеем
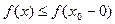 при
при 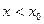
и
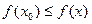 при
при 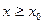 .
.
Поэтому в случае (4) функция  не принимает значений из интервала
не принимает значений из интервала
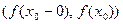 ,
,
но принимает значения как слева от него, так и справа. Аналогично устанавливается, что в случае (5) функция  не принимает значений из интервала
не принимает значений из интервала
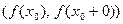 ,
,
но принимает значения как слева от него, так и справа. В обоих случаях множество значений функции  не может быть отрезком. Полученное противоречие и доказывает теорему?
не может быть отрезком. Полученное противоречие и доказывает теорему?
Теорема 4 (об обратной функции к непрерывной, строго монотонной). Пусть функция  непрерывна и строго монотонна на отрезке
непрерывна и строго монотонна на отрезке 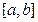 . Тогда существует обратная к ней функция
. Тогда существует обратная к ней функция 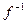 , которая является непрерывной и строго монотонной в том же смысле, что и функция
, которая является непрерывной и строго монотонной в том же смысле, что и функция  .
.
Д о к а з а т е л ь с т в о. Для определенности пусть функция  возрастает на отрезке
возрастает на отрезке 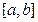 . В этом случае множество ее значений является отрезком
. В этом случае множество ее значений является отрезком 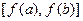 . Тогда, очевидно, она, как отображение
. Тогда, очевидно, она, как отображение
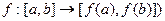
является взаимно-однозначным отображением «на» и, следовательно, имеет обратную функцию 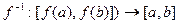 . Покажем, что она возрастающая.
. Покажем, что она возрастающая.
Предположим противное. Тогда найдутся такие 
 ,
, 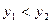 , что
, что 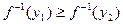 . Но в этом случае
. Но в этом случае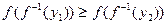 , т.е.
, т.е. 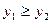 , а это противоречит тому, что
, а это противоречит тому, что 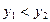 .
.
Наконец, поскольку множество значений монотонной функции 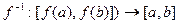 является отрезком, то по теореме 3 она непрерывна на отрезке
является отрезком, то по теореме 3 она непрерывна на отрезке 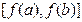 ?
?
Очевидно, справедливо следующее обобщение теоремы 4.
Следствие. Пусть функция  непрерывна и строго монотонна на произвольном промежутке
непрерывна и строго монотонна на произвольном промежутке 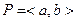 . Тогда обратная к ней функция непрерывна и строго монотонна в том же смысле на промежутке
. Тогда обратная к ней функция непрерывна и строго монотонна в том же смысле на промежутке 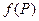 .
.
 2014-02-09
2014-02-09 16071
16071
