Оператор момента импульса

В атомах и молекулах момент импульса и связанный с ним магнитный момент могут создаваться за счет орбитального движения электронов. По этой причине момент импульса называется также орбитальным моментом. Описание свойств системы на таком микроскопическом уровне возможно только с помощью аппарата квантовой механики. При переходе к квантовой механике классическое выражение для механического момента импульса (1.4) заменяется квантовомеханическим оператором. Так как оператор импульса частицы есть 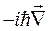, оператор момента импульса одной частицы должен иметь вид 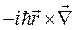. Обычно момент импульса измеряется в единицах постоянной Планка 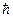. Тогда оператор момента для системы частиц есть

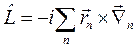(1.10)

Для системы, находящейся во внешнем поле, момент импульса в общем случае не сохраняется. Закон сохранения имеет, однако, место для центрально-симметричного поля. Таким типом симметрии - обладают свободные атомы.

Если момент импульса не сохраняется, можно поставить вопрос о среднем его значении. Квантовомеханическое среднее определяется интегралом

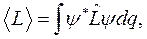(1.11)

где 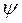- волновая функция системы, a q - набор всех пространственных координат. Можно показать, что для всякого невырожденного состояния в отсутствие внешнего магнитного поля 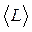= 0. Это следует из того, что гамильтониан системы 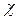является в этом случае действительным. Тогда уравнение Шредингера 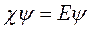при операции комплексного сопряжения переходит в уравнение 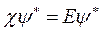. Из условия невырожденности состояния следует тогда, что 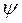и 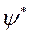могут отличаться друг от друга лишь несущественным фазовым множителем с модулем, равным единице, т.е. если этот множитель не учитывать, волновая функция 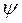должна быть вещественной. Так как выражение (1.10) является чисто мнимым, среднее значение (1.11) также должно быть мнимым. С другой стороны, среднее значение любой измеряемой физической величины может быть только действительным. Отсюда и следует, что это значение может равняться только нулю.

Напомним теперь основные свойства оператора момента.

Различные проекции оператора удовлетворяют следующим правилам коммутации:

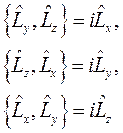(1.12)

Так как разные проекции не коммутируют между собой, они не могут одновременно иметь определенных значений.

Из операторов 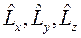можно составить оператор квадрата величины момента импульса

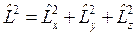(1.13)

Этот оператор коммутирует со всеми проекциями

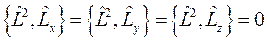(1.14)

Это означает, что квадрат момента может иметь определенное значение одновременно с проекцией на одну из осей.

Пусть такой осью будет ось Z. Собственные функции операторов 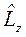и 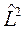определяются целыми квантовыми числами М и L соответственно. Обозначим эти собственные функции как 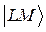. Тогда

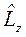
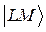= М ,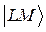

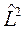
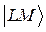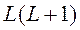
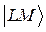= (1.15)

Причем L 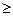0, а М меняется от -L до L с шагом 1. Явный вид собственных функций дается сферическими гармониками 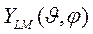, они зависят только от полярных координат, 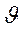и 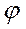сферической системы координат.

Полезно ввести операторы

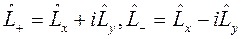(1.16)

Отличные от нуля матричные элементы этих операторов

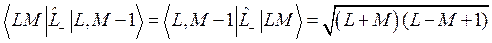(1.17)

Операторы 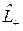и 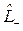называются соответственно операторами повышения и понижения. Действительно, согласно (1.17), первый из них при действии на волновую функцию повышает квантовое число М, а второй понижает.

Отметим также полезную формулу, используемую при расчете скалярного произведения двух операторов:

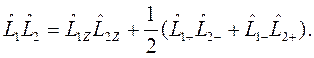(1.18)

Наконец, можно ввести оператор магнитного момента, который по аналогии с (1.3) есть

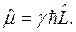(1.19)

Таким образом, магнитный момент за счет орбитального движения является величиной, кратной константе

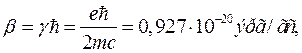(1.20)

где е и m - заряд и масса электрона соответственно (е > 0). Константа 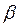называется магнетоном Бора.

В молекулах сферическая, симметрия поля не имеет места, и можно говорить только о среднем значении орбитального момента. Оказывается, что за очень редким исключением основное состояние молекул является невырожденным по орбитальным квантовым числам (вырождение может быть по спину (п. 1.4)). Отсюда, согласно вышеизложенному, следует, что 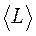= 0. Поэтому в магнитном резонансе молекул оператор орбитального момента и связанный с ним магнитный момент важны только при вычислении разного рода поправок к эффектам, обусловленным наличием у частиц спинового магнитного момента [[1]].

1.3. Магнитные моменты электрона и ядер.

Свободный электрон и многие ядра обладают спином. Спин - это "собственный" момент частицы, не связанный с ее движением в пространстве. Величина эта векторная. Измеряется спин, как и орбитальный момент, в единицах постоянной Планка 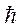. Оператор спина имеет все те же свойства, что и оператор орбитального момента за исключением зависимости собственных функций от пространственных координат. Также он отличается тем, что может иметь значения, кратные 1/2, т.е. 1/2, 1, 3/2 и т.д. Спины ядер мы будем обозначать буквой I, а спины электрона - буквой S. -Для краткости в дальнейшем мы не будем использовать шляпку над оператором спина.

Частица со спином имеет также магнитный момент. Для ядер и свободного электрона связь между спиновым и магнитным моментами дается в виде, аналогичном выражению (1.19) для орбитального момента:

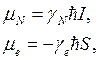(1.21)

где 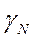и 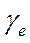- гиромагнитные отношения для данного ядра (для разных ядер оно разное) и свободного электрона соответственно. Их величины отличаются от гиромагнитного отношения для орбитального момента. Прежде чем их здесь приводить, укажем, что вместо гиромагнитного отношения используются также и другие константы:

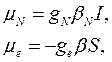(1.22)

где g_N и g_e - безразмерные константы, называемые g -фактором (соответственно ядра и свободного электрона), 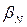- ядерный магнетон,

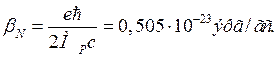(1.23)

Здесь 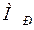- масса протона. Константа 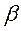- введенный ранее магнетон Бора (1.20). Константы связаны соотношениям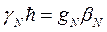и и 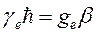. Знак минус для электрона связан с его отрицательным зарядом.

Для свободного электрона g -фактор получается теоретически из релятивистского уравнения Дирака. Он равен 2,0023. Соответственно .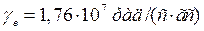

Для ядер величина g_N (или 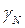) может быть получена только из эксперимента. Величины спинов и констант g_N и 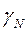для некоторых ядер приведены в табл. 1. Здесь же даны значения квадрупольного момента Q, которым обладают ядра со спином I > 1/2. Отметим, что все ядра с нечетным массовым числом имеют полуцелый спин. У ядер с четным массовым числом спин целый. Если заряд ядра тоже четный, то спин равен нулю (например, у 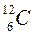). Ядра с ненулевым спином называются часто магнитными.

Таблица 2

Магнитные параметры ядер

Ядро	I	Естеств. содерж., %		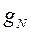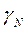, рад/с∙гс	Q, 10-24 см-2
1Н	1/2	99,98	5,585		-
2Н		0,015	0,857		0,00274
13С	1/2	1,108	1,405		-
14N		99,63	0,403		0,02
15N	1/2	0,37	-0,567	-2712	-
19F	1/2		5,257		-
31P	1/2		2,263		-
35Cl	3/2	75,53	0,548		-0,079
37Cl	3/2	24,47	0,456		-0,062

Отметим, что во вcех органических веществах содержатся магнитные

ядра. Это протоны и ядра ¹³С.

Электрон имеет спин, равный 1/2. В подавляющем большинстве окружающих нас химических соединений спины электронов спарены друг с другом, т.е. их молекулы имеют полный спин, равный нулю. Имеется, однако, целый ряд важных классов соединений, в которых присутствуют неспаренные электроны. Такими соединениями являются промежуточные продукты химических превращений: свободные атомы (например, Н, Сl и т.д.) и свободные радикалы (ОН, СН₃ и т.д.). Причем свободные радикалы в некоторых случаях могут быть очень стабильными. Присутствуют они, например, в ископаемом природном угле, черноземе почв, атмосферных аэрозолях. В настоящее время в научных исследованиях широко используются специально синтезированные стабильные радикалы: спиновые зонды и метки. Другим важным классом являются соединения переходных металлов (железа, меди, марганца и т.д.). Причем в этих соединениях могут присутствовать сразу несколько неспаренных электронов с суммарным спином S > 1/2. (В некоторых органических радикалах также может быть несколько неспаренных электронов с суммарным спином S > 1/2.) Имеются и другие интересные объекты, в структуре которых присутствуют неспаренные электроны.