Кинетические уравнения для населенностей

В рассматриваемой двухуровневой системе, кроме переходов, вызванных переменным магнитным полем 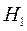, возможны также переходы, обусловленные взаимодействием спина со своим окружением в веществе, так как это взаимодействие из-за тепловых флуктуации зависит от времени. Вероятности этих переходов вверх и вниз не равны друг другу (из-за наличия спонтанного испускания с верхнего уровня), что и приводит к установлению больцмйновского равновесия в системе. Схематически эти переходы показаны на рис 3.

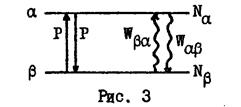
В равновесии без внешнего воздействия (Р = 0) количество частиц, совершающих переходы вверх и вниз, должно быть одинаковым, т.е. должно выполняться соотношение

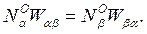(1.34)

Поэтому

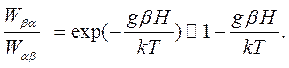(1.35)

Кинетические уравнения для населенностей имеют вид

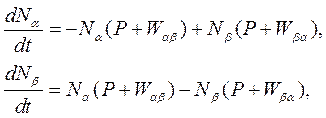(1.36)

Введем среднюю вероятность спонтанных переходов

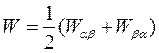. (1.37)

Тогда с учетом (1.35)

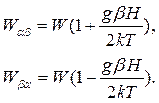(1.38)

Теперь кинетические уравнения (1.36) можно переписать в виде

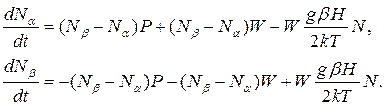(1.39)

Вычтем здесь из второго уравнения первое. Обозначив также 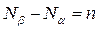, 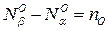и приняв во внимание (1.31), получаем

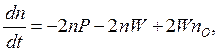(1.40)

или

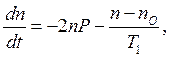(1.41)

где введено время Т₁ = 1/2W. Это время называется временем спин-решеточной релаксации. Оно определяет скорость установления теплового равновесия в спиновой системе за счет обмена энергией с окружающей средой (под решеткой в магнитном резонансе принято понимать среду, в которой находится спин, независимо от того, является ли эта среда твердой, жидкой или газообразной). При равновесии, когда 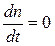, из (1.41) получаем

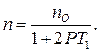(1.42)

При большой напряженности Н₁ переменного поля, вызывающего переходы между уровнями, когда РТ₁» 1 (накачка уровней), разность населенностей n стремится к нулю. Так как измеряемый сигнал резонансного поглощения пропорционален произведению P_n, этот сигнал при больших Р выходит на предельное значение. Это явление называется насыщением магнитного резонанса. Оно означает, чтo при больших мощностях накачки уровней спиновая система не успевает отдавать получаемую энергию в решетку. Чтобы избежать насыщения, необходимо работать при малых Н₁ [1].