Для получения количественной информации о субструктуре нанокристаллических сплавов [[2]] большие возможности имеет метод малоуглового рассеяния рентгеновских лучей (МУР). Этот метод позволяет определить размеры и форму субмикроскопических частиц размеры, которых лежат в пределах от 10 до 1000 Å. К преимуществам метода МУР следует отнести то, что в области малых углов можно не учитывать комптоновское рассеяние, а также рассеяние вследствие тепловых колебаний и статических смещений, которые ничтожно малы именно в области малых углов. Следует отметить, что в создании дифракционной картины принимают участие лишь электроны (рассеяния на ядрах пренебрежимо мало), поэтому по дифракционной картине можно судить о пространственном распределении электронной плотности, причем избыток и недостаток электронов по отношению к средней по образцу электронной плотности действуют эквивалентно [[3]].
Согласно классической теории [4] амплитуда рассеянная отдельной сферической частицей равна
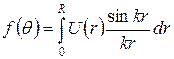 , (2.1)
, (2.1)
где 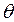 – угол дифракции, модуль вектора дифракции равен
– угол дифракции, модуль вектора дифракции равен 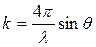 ;
; 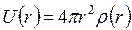 – функция распределения электронной плотности в частице;
– функция распределения электронной плотности в частице; 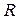 – радиус частицы.
– радиус частицы.
Наиболее легко может быть вычислена интенсивность, рассеянная однородной сферической частицей радиуса 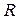 имеющей электронную плотность
имеющей электронную плотность 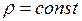 .
.
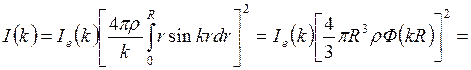
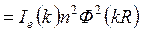 , (2.2)
, (2.2)
где
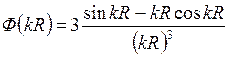 , (2.3)
, (2.3)
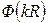 – функция формы частицы, а ее квадрат
– функция формы частицы, а ее квадрат 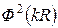 – фактор рассеяния сферической частицы;
– фактор рассеяния сферической частицы; 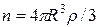 – число электронов в частице,
– число электронов в частице, 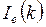 – интенсивность, рассеиваемая электроном (следует заметить, что в области нулевого узла обратной решетки угловой зависимостью функции
– интенсивность, рассеиваемая электроном (следует заметить, что в области нулевого узла обратной решетки угловой зависимостью функции 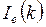 можно пренебречь, т.е.
можно пренебречь, т.е. 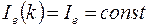 ).
).
Как показано в [2], Гинье предложил упрощенный метод расчета интенсивности, который заключается в том, что при малом размере частицы и при 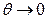 , имеем
, имеем 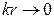 . Поэтому при разложении
. Поэтому при разложении 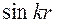 в ряд, можно ограничиться первыми двумя членами:
в ряд, можно ограничиться первыми двумя членами:
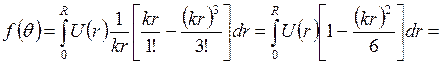
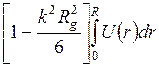 , (2.4)
, (2.4)
где
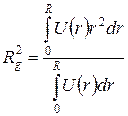 . (2.5)
. (2.5)
Величина 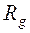 называется электронным радиусом инерции (радиус гирации) частицы и представляет собой среднеквадратичный размер частицы (неоднородности). Легко показать, что для однородной сферической частицы радиуса
называется электронным радиусом инерции (радиус гирации) частицы и представляет собой среднеквадратичный размер частицы (неоднородности). Легко показать, что для однородной сферической частицы радиуса 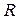 имеющей электронную плотность
имеющей электронную плотность 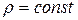 , радиус гирации
, радиус гирации 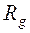 выражается через ее радиус
выражается через ее радиус 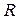 следующим образом:
следующим образом: 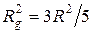 , а величина
, а величина 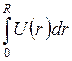 равна
равна 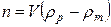 – числу электронов в частице или точнее – разности между числом электронов в частице и числом электронов в равном объеме окружающей частицу среды (
– числу электронов в частице или точнее – разности между числом электронов в частице и числом электронов в равном объеме окружающей частицу среды (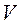 – объем неоднородности,
– объем неоднородности, 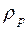 и
и 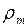 – электронные плотности вещества неоднородности и матрицы соответственно). Исходя из выше сказанного, получим:
– электронные плотности вещества неоднородности и матрицы соответственно). Исходя из выше сказанного, получим:
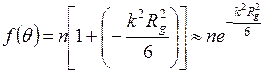 . (2.6)
. (2.6)
В случае монодисперсной разряженной системы, когда можно пренебречь интерференцией лучей, рассеянных различными частицами, профиль интенсивности рассеяния нулевого узла обратной решетки системой, содержащей 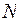 частиц в облучаемом объеме, можно описать следующей формулой:
частиц в облучаемом объеме, можно описать следующей формулой:

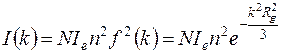 . (2.7)
. (2.7)
Эта формула (2.7) была получена Гинье и названа его именем.
Величина 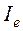 находится по формуле:
находится по формуле:
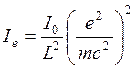 ,
,
где 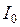 – интенсивность первичного пучка;
– интенсивность первичного пучка; 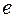 и
и 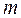 – заряд и масса электрона соответственно;
– заряд и масса электрона соответственно; 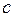 – скорость света в вакууме;
– скорость света в вакууме; 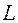 – расстояние от образца до точки наблюдения.
– расстояние от образца до точки наблюдения.
Как показано на рис. 4 зависимости интенсивности от угла, вычисленные по формулам (2.2) и (2.7) для сферически однородной частицы радиуса 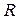 хорошо совпадают при
хорошо совпадают при 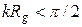 .
.
 |
Рис. 4. Рассеяние сферической частицей радиуса 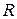 . . |
Прологарифмируем формулу Гинье:
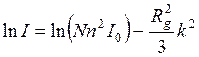 . (2.8)
. (2.8)
Таким образом, из выражения (2.8) следует, что в случае представлении картины МУР от монодисперсной системы частиц в координатах 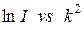 при достаточно малых
при достаточно малых 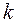 получается линейная зависимость, по углу наклона
получается линейная зависимость, по углу наклона 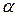 которой можно найти радиус гирации
которой можно найти радиус гирации 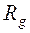 частиц.
частиц.
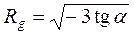 (2.9)
(2.9)
В случае полидисперсной системы, когда частицы имеют разные размеры, зависимость 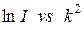 уже не будет линейной. Однако, как показывают исследования при достаточной монодисперсности каждого сорта частиц и отсутствия межчастичной интерференции на картине МУР в координатах
уже не будет линейной. Однако, как показывают исследования при достаточной монодисперсности каждого сорта частиц и отсутствия межчастичной интерференции на картине МУР в координатах 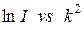 можно выделить несколько линейных областей. Разделив эти области можно найти соответствующие им радиусы гирации частиц разного сорта (рис. 5).
можно выделить несколько линейных областей. Разделив эти области можно найти соответствующие им радиусы гирации частиц разного сорта (рис. 5).
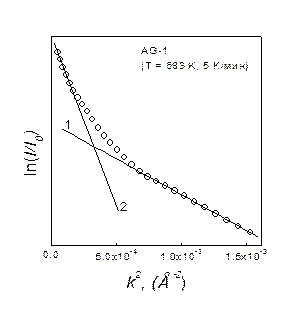 |
Рис 5. Интенсивность МУР в координатах 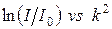 от частично кристаллизованного Al86Ni6Co2Gd6 сплава: 1 – соответствует среднему радиусу от частично кристаллизованного Al86Ni6Co2Gd6 сплава: 1 – соответствует среднему радиусу 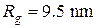 , а 2 – линейная область соответствует , а 2 – линейная область соответствует 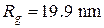 . . |
Не смотря на выше перечисленные достоинства при получении структурной информации, метод МУР обладает рядом существенных недостатков [3].
Значительное искажение в картину МУР может внести двойное брэгговское отражение (ДБО), которое возникает при прохождении рентгеновских лучей через кристаллические материалы. Схема, объясняющая возникновение ДБО, приведена на рис. 6. Пусть первичный пучок рентгеновских лучей падает на мозаичный кристалл, состоящий из слегка разориентированных блоков. Если, например, блок 1 находится к s0 под брегговским углом υ, то от него отразится луч s1, который на своем пути может встретить блок 2, находящийся по отношению к s1 в отражающем положении, поэтому от блока 2 отразится луч s2. Если нормали n1 и n2 к отражающим плоскостям обоих блоков расположены в одной плоскости (например, в плоскости чертежа), то луч s2 попадет, как и луч s1, в центральное пятно P0 рентгенограммы. Блок 2 отражает и в том случае, когда он повернут вокруг s1 так, что нормаль n2 продолжает составлять угол (π/2)- υ с s1, но уже не лежит в одной плоскости с n1. Тогда дважды отраженный луч выйдет из плоскости чертежа и переместится по образующей конуса, осью которого является s1. В результате на фотопленке около центрального пятна P0 появится короткий штрих, являющийся наложением следов дважды отраженных лучей.
 |
| Рис 6. Схема, поясняющая возникновение двойного брегговского отражения. |
Штрихи ДБО ориентированы перпендикулярно к линии P0P, соединяющей центральное пятно P0 с брегговским максимумом P; их длина тем больше, чем больше угол мозаичности кристалла.
Избавиться от ДБО при исследовании МУР монокристаллом несложно: достаточно ориентировать последний по отношению к первичному пучку так, чтобы ни одна система плоскостей (hkl) не находилась в отражающем положении.
При исследовании поликристаллов исключить ДБО практически нельзя, так как всегда найдутся кристаллиты, отражающие первичный пучок. ДБО будет отсутствовать только при использовании излучений с длиной волны λ > dmax (dmax – наибольшее межплоскостное расстояние для данного кристаллита). Так, например, при исследовании меди следует применять Al Kα – излучение, что представляет значительные экспериментальные трудности.
При сравнительно больших углах рассеяния (ε > 10') МУР нельзя отделить от эффекта ДБО. Но при ε < 2' интенсивность МУР на порядок выше интенсивности ДБО. Отделение истинного МУР от ДБО в этом случае основано на различном характере зависимостей МУР и ДБО от используемой длины волны. Для этого получают кривые интенсивности I (ε/λ) на двух излучениях, например, CrKα и CuKα. Если обе кривые совпадают, то это свидетельствует, что все рассеяние обусловлено эффектом МУР. Если кривые разойдутся так, что в каждой точке ε/λ отношение интенсивностей окажется постоянным, то все рассеяние обусловлено ДБО.
Когда присутствуют оба эффекта, то
I1 = I1ДБО + I1ДБО; I2 = I2ДБО + I2ДБО
Б. Я. Пинесом и др. показано, что поскольку при ε1/λ1 = ε2/λ2
I1МУР/I2МУР = 1 и I1ДБО/I2ДБО = К,
I2ДБО = (I1 – I2)ε1/λ1 = ε2/λ2 (К – 1),
где постоянную К вычисляют теоретически для каждого конкретного случая.
По эффекту ДБО можно определить средние углы разориентации блоков внутри кристаллитов или монокристаллах [[4]].
Исследование МУР представляет собой значительные экспериментальные трудности, так как обычные пучки рентгеновских лучей, вырезаемые щелями, имеют заметную расходимость, а паразитное рассеяние на щелях может полностью скрыть эффект МУР; сложно также регистрировать МУР из-за его малой интенсивности.
Паразитное рассеяние от кромок фокусирующих щелей вносит существенные погрешности, поэтому необходимо снимать картины при двух положениях образца рассевающем и поглощающем. Для увеличения интенсивности первичного пучка применяют щелевую коллимацию, что приводит к размытию интенсивности и при обработке в экспериментально полученную зависимость необходимо вносить поправку по формуле
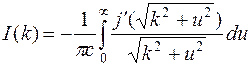 , (2.10)
, (2.10)
где 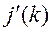 и
и 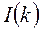 – экспериментальная и исправленная интенсивности МУР,
– экспериментальная и исправленная интенсивности МУР, 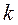 – вектор дифракции,
– вектор дифракции, 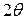 – угол рассеяния,
– угол рассеяния, 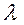 – длина волны;
– длина волны; 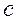 – постоянный коэффициент;
– постоянный коэффициент; 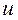 – переменная интегрирования [2]. Следует также отметить, что формулу Гинье можно обосновано применять лишь в случаях предусматривающих отсутствие интерференции лучей рассеянных различными частицами, простоту форм и электронную однородность рассеивающих частиц (шар, эллипс, пластинка при
– переменная интегрирования [2]. Следует также отметить, что формулу Гинье можно обосновано применять лишь в случаях предусматривающих отсутствие интерференции лучей рассеянных различными частицами, простоту форм и электронную однородность рассеивающих частиц (шар, эллипс, пластинка при 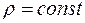 ), в противном случае зависимость
), в противном случае зависимость 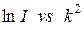 не будет содержать линейных областей, и обработка картин МУР существенно усложняется [5].
не будет содержать линейных областей, и обработка картин МУР существенно усложняется [5].
Одной из наиболее удачных камер, устраняющих паразитное рассеяние на щелях, является камера Кратки (рис. 7). В этой камере вместо щелей используются плоскопараллельные металлические пластинки (1 — 4) с хорошо отполированной поверхностью (стальные мерительные плиты). Зазор между плитами 1 и 2 равен ~ 0,01 мм. Расходящийся пучок рентгеновских лучей проходит через образец 5 и дает на фотопленке 6 след РР'. Картина МУР регистрируется на фотопленке выше следа РР' (заштрихованный участок), где паразитное рассеяние практически отсутствует. Для исключения рассеяния на воздухе камеру Кратки монтируют в цилиндре, снабженном съемными крышками с вакуумными прокладками. Во время съемки воздух из цилиндра откачивают вакуумным насосом [4].
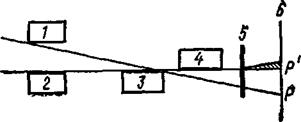 |
| Рис 7. Схема камеры Кратки. |
2.2. Анализ нанокомпозитной структуры методами рентгеновской дифракции на большие и малые углы.
Среди косвенных методов определения размера частиц основное место принадлежит дифракционному методу. Одновременно этот метод является наиболее простым и доступным, так как рентгеновское исследование структуры распространено повсеместно и хорошо обеспечено соответствующей аппаратурой. С помощью дифракционного метода наряду с фазовым составом, параметрами кристаллической решётки, статическими и динамическими смещениями атомов из положения равновесия и микронапряжениями в решётке можно определить размер зёрен (кристаллитов).
Определение дифракционным методом размера зёрен, частиц (или областей когерентного рассеяния) основано на изменении формы профиля дифракционного отражения при уменьшении размера зёрен. При обсуждении дифракции под когерентным рассеянием понимается рассеяние дифрагирующего излучения, при котором обеспечивается выполнение условий интерференции. В общем случае размер отдельного зерна может не совпадать с размером области когерентного рассеяния.
В дифракционных экспериментах изучение дефектов структуры проводят по уширению дифракционных отражений от поликристалла или порошка. Однако при практическом применении этого метода для определения размера зёрен зачастую сравнивают ширину дифракционных отражений от вещества с крупным размером зёрен (частиц) и от того же вещества в наносостоянии. Такое определение уширения и последующая оценка среднего размера частиц не всегда верны и могут давать очень большую (несколько сотен процентов) ошибку. Дело в том, что уширение следует определять относительно дифракционных отражений от бесконечно большого кристалла. Реально это означает, что сравнивать измеренную ширину дифракционных отражений следует с инструментальной шириной, т. е. с шириной функции разрешения дифрактометра, заранее определенной в специальном дифракционном эксперименте. Кроме того, точное определение ширины дифракционных отражений возможно только путем теоретического восстановления формы экспериментального отражения. Весьма существенно, что могут быть и другие, помимо малого размера кристаллитов, физические причины уширения дифракционных отражений. Поэтому важно не только определить величину уширения, но и выделить вклад в него, обусловленный именно малым размером частиц.
Поскольку дифракционный метод определения размера частиц является самым распространенным и доступным, рассмотрим особенности его применения более подробно [[5]].
Ширина дифракционной линии может зависеть от ряда причин. К ним относятся малые размеры кристаллитов, наличие разного рода дефектов, а так же неоднородность образцов по химическому составу. Уширение, обусловленное микродеформациями и хаотически распределенными дислокациями, зависит от порядка отражения и пропорционально tg υ. Величина уширения, вызванного негомогенностью Δ х; (или Δу), пропорциональна (sin2 υ)/cos υ. В случае нанокристаллических веществ наиболее интересно уширение, связанное с малым размером D кристаллитов (D < 150 нм), причем в этом случае величина уширения пропорциональна seс υ. Рассмотрим вывод выражения, учитывающего уширение дифракционного отражения, обусловленное конечным размером частиц поликристаллического вещества.
Пусть <l>v — усреднённая по объёму высота колонки плоскостей когерентного рассеяния, <D> — усреднённый по объёму диаметр частиц. Для частиц со сферической формой интегрирование приводит к выражению
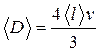 (2.11)
(2.11)
Введем в рассмотрение вектор рассеяния s = 2sin υ / λ, где λ — длина волны излучения. Математически его дифференциал (или неопределенность с физической точки зрения, поскольку в конечном кристалле волновой вектор становится плохим квантовым числом) равен
ds= 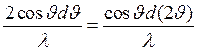 ( 2.12)
( 2.12)
В этом выражении величина d(2υ) является интегральной шириной дифракционного отражения (линии), выраженной в углах 2υ и измеряемой в радианах. Интегральная ширина определяется как интегральная интенсивность линии, деленная на её высоту, и не зависит от формы дифракционной линии. Это позволяет использовать интегральную ширину для анализа дифракционного рентгеновского, синхротронного или нейтронографического эксперимента, выполненного на разных установках с отличающейся функцией разрешения дифрактометра и в разных интервалах углов.
Неопределенность вектора рассеяния ds обратно пропорциональна усреднённой по объёму высоте колонки плоскостей когерентного рассеяния <l>v, поэтому произведение этих величин равно единице, <l>v·ds = 1. Из этого соотношения ясно, что при бесконечной высоте колонки (т. е. при бесконечно большом размере кристаллитов) неопределенность ds равна нулю. Если же высота колонки мала и стремится к нулю, то неопределенность ds волнового вектора и, соответственно, ширина d (2υ) дифракционной линии становятся очень большими. Поскольку <l>v = 1/ds, то для дифракционной линии произвольной формы размер зерна (в предположении, что все зёрна являются сферическими) с учётом (2.11) и (2.12) можно определить как
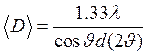 (2.13)
(2.13)
где d (2 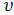 ) — интегральная ширина дифракционной линии. На практике часто пользуются не интегральной шириной, а полной шириной дифракционной линии на половине высоты FWHM (full width at half maximum). Связь между интегральной шириной линии и FWHM зависит от формы экспериментальной дифракционной линии и в каждом конкретном случае должна определяться специально. Для линии в виде прямоугольника и треугольника интегральная ширина линии в точности равна FWHM. Для функций Лоренца и Гаусса связь описывается выражениями: d (2
) — интегральная ширина дифракционной линии. На практике часто пользуются не интегральной шириной, а полной шириной дифракционной линии на половине высоты FWHM (full width at half maximum). Связь между интегральной шириной линии и FWHM зависит от формы экспериментальной дифракционной линии и в каждом конкретном случае должна определяться специально. Для линии в виде прямоугольника и треугольника интегральная ширина линии в точности равна FWHM. Для функций Лоренца и Гаусса связь описывается выражениями: d (2 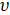 )L ≈ 1,6∙FWHML(2
)L ≈ 1,6∙FWHML(2 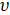 ) и d (2
) и d (2 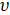 )G ≈ 1,1∙FWHMG(2
)G ≈ 1,1∙FWHMG(2 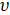 ), а для псевдо-функции Фойгта, которая будет рассмотрена ниже, эта связь более сложная и зависит от соотношения вкладов Гаусса и Лоренца. Для дифракционных линий в малых углах соотношение между интегральным уширением и FWHM можно принять равным d(2
), а для псевдо-функции Фойгта, которая будет рассмотрена ниже, эта связь более сложная и зависит от соотношения вкладов Гаусса и Лоренца. Для дифракционных линий в малых углах соотношение между интегральным уширением и FWHM можно принять равным d(2 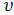 ) ≈ 1,47 ∙ FWHM(2
) ≈ 1,47 ∙ FWHM(2 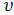 ); подставляя это соотношение в (2.13), получим формулу Дебая:
); подставляя это соотношение в (2.13), получим формулу Дебая:

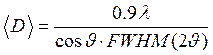 (2.14)
(2.14)
В общем случае, когда частицы вещества имеют произвольную форму, средний размер частиц можно найти по формуле Дебая-Шеррера:
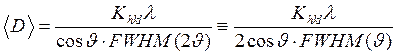 (2.15)
(2.15)
где 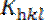 — постоянная Шеррера, значение которой зависит от формы частицы (кристаллита, домена) и от индексов (hkl) дифракционного отражения.
— постоянная Шеррера, значение которой зависит от формы частицы (кристаллита, домена) и от индексов (hkl) дифракционного отражения.
В реальном эксперименте из-за конечного разрешения дифрактометра линия уширяется и не может быть меньше, чем инструментальная ширина линии. Иначе говоря, в формуле (2.15) следует использовать не ширину FWHM(2υ) отражения, а её уширение β относительно инструментальной ширины. Поэтому в дифракционном эксперименте средний размер частиц определяют по методу Уоррена:
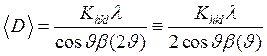 (2.16)
(2.16)
где 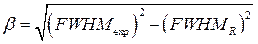 уширение дифракционного отражения. Заметим, что
уширение дифракционного отражения. Заметим, что 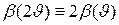 .
.
Полную ширину на половине высоты FWHMRили инструментальную ширину дифрактометра можно измерить на хорошо отожжённом и полностью гомогенном веществе (порошке) с частицами размером 1-10 мкм. Иначе говоря, за эталон сравнения нужно брать отражение без каких-либо дополнительных, кроме инструментального, уширений. Если функция разрешения дифрактометра описывается функцией Гаусса, a υR — её второй момент, то FWHMR=2.355υR.
Дифракционные отражения описывают функциями Гаусса g(υ) и Лоренца l(υ):
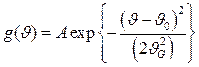 , (2.17)
, (2.17)
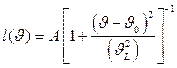 . (2.18)
. (2.18)
или их суперпозицией V 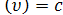 l (
l (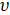 ) + (1-c) g(
) + (1-c) g(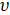 ) - псевдо-функцией Фойгта:
) - псевдо-функцией Фойгта:
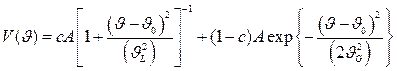 , (2.19)
, (2.19)
где 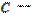 относительный вклад функции Лоренца в общую интенсивность отражения;
относительный вклад функции Лоренца в общую интенсивность отражения; 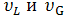
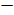 параметры распределений Лоренца и Гаусса; А — нормирующий множитель.
параметры распределений Лоренца и Гаусса; А — нормирующий множитель.
Рассмотрим особенности распределений Гаусса и Лоренца, которые необходимы далее. Для распределения Гаусса параметр 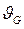 является вторым моментом функции. Второй момент
является вторым моментом функции. Второй момент 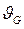
 , выраженный в углах
, выраженный в углах 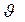 , связан с полной шириной на половине высоты, измеренной в углах 2
, связан с полной шириной на половине высоты, измеренной в углах 2 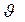 , известным соотношением
, известным соотношением 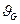 (
(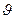 ) = FWHM(2
) = FWHM(2 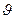 )/(2·2,355). Это соотношение легко получить непосредственно из распределения Гаусса. На рис. 6 а показано распределение Гаусса, описываемое функцией
)/(2·2,355). Это соотношение легко получить непосредственно из распределения Гаусса. На рис. 6 а показано распределение Гаусса, описываемое функцией
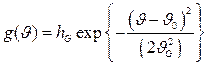 , (2.20)
, (2.20)
где 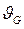 — второй момент функции Гаусса, т. е. значение аргумента, соответствующее точке перегиба функции, когда
— второй момент функции Гаусса, т. е. значение аргумента, соответствующее точке перегиба функции, когда 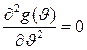 . Найдем величину
. Найдем величину 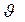 , при которой функция (2.20) принимает значение, равное половине её высоты. В этом случае
, при которой функция (2.20) принимает значение, равное половине её высоты. В этом случае 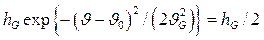 и
и 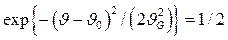 , откуда
, откуда 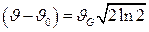 . Как видно на рисунке 6 а, полная ширина функции Гаусса на половине высоты равна
. Как видно на рисунке 6 а, полная ширина функции Гаусса на половине высоты равна 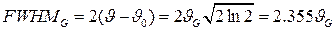 .
.
 |
Рис 8. Распределения Гаусса g(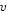 ) и Лоренца l ( ) и Лоренца l (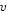 ), используемые для модельного описания формы дифракционных линий: а – связь между вторым моментом ), используемые для модельного описания формы дифракционных линий: а – связь между вторым моментом 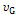 функции Гаусса и полной шириной функции g( функции Гаусса и полной шириной функции g(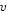 ) на половине её высоты FWHMg; б — для функции Лоренца параметр ) на половине её высоты FWHMg; б — для функции Лоренца параметр 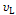 = FWHMl/2, второй момент функции l ( = FWHMl/2, второй момент функции l (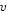 ) равен ) равен 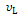 / / 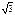 . . |
Для распределения Лоренца параметр 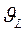 совпадает с полушириной этой функции на половине высоты. Пусть функция Лоренца,
совпадает с полушириной этой функции на половине высоты. Пусть функция Лоренца,
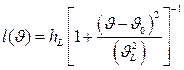 , (2.21)
, (2.21)
принимает значение, равное половине высоты, т. е. 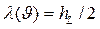 (рис. 6 б). Значение аргумента, которое соответствует такому значению функции, найдем из уравнения
(рис. 6 б). Значение аргумента, которое соответствует такому значению функции, найдем из уравнения
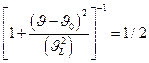 ,
,
откуда 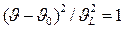 и
и 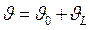 .Таким образом, действительно для функции Лоренца
.Таким образом, действительно для функции Лоренца 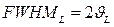 . Второй момент функции Лоренца, т. е. значение аргумента, соответствующего точке перегиба функции, можно найти из условия
. Второй момент функции Лоренца, т. е. значение аргумента, соответствующего точке перегиба функции, можно найти из условия 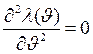 . Расчет показывает, что второй момент функции Лоренца равен
. Расчет показывает, что второй момент функции Лоренца равен 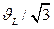 .
.
Псевдо-функция Фойгта (2.19) обеспечивает наилучшее по сравнению с функциями Гаусса и Лоренца описание экспериментального дифракционного отражения.
Учитывая это, функцию разрешения дифрактометра 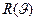 представим как псевдо-функцию Фойгта; для упрощения записи примем, что в (2.19) А=1. Тогда
представим как псевдо-функцию Фойгта; для упрощения записи примем, что в (2.19) А=1. Тогда
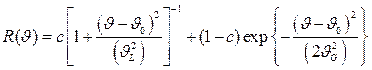 . (2.22)
. (2.22)
Поскольку функция разрешения есть суперпозиция функций Лоренца и Гаусса, то в нулевом приближении ее ширину можно аппроксимировать выражением
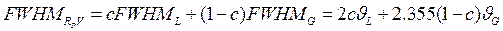 . (2.23)
. (2.23)
Если 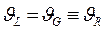 , то
, то 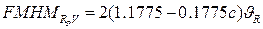 . Пусть некоторая эффективная функция Гаусса
. Пусть некоторая эффективная функция Гаусса 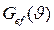 , площадь которой совпадает с площадью псевдо-функции Фойгта, имеет ширину
, площадь которой совпадает с площадью псевдо-функции Фойгта, имеет ширину 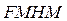 , равную
, равную 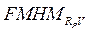 , тогда второй момент такой функции
, тогда второй момент такой функции 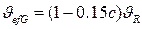 . Таким образом псевдо-функция разрешения Фойгта
. Таким образом псевдо-функция разрешения Фойгта 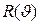 и эффективная функция Гаусса
и эффективная функция Гаусса 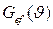 эквивалентны по полуширине. Это позволяет, в нулевом приближении, заменить функцию (2.22) функцией
эквивалентны по полуширине. Это позволяет, в нулевом приближении, заменить функцию (2.22) функцией
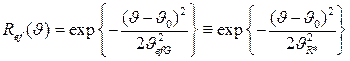 , (2.24)
, (2.24)
где 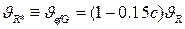 при условии, что
при условии, что 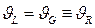 .
.
Экспериментальная функция 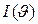 , описывающая форму произвольного дифракционного отражения, является сверткой функции распределения
, описывающая форму произвольного дифракционного отражения, является сверткой функции распределения 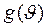 и функции разрешения
и функции разрешения 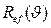 (2.24), т. е.
(2.24), т. е.
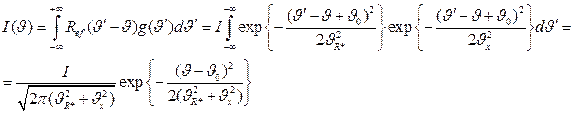 (2.25)
(2.25)
Из (2.25) ясно, что второй момент 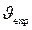 экспериментальной функции
экспериментальной функции 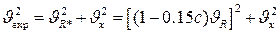 . (2.26)
. (2.26)
Уширение β дифракционного отражения выражается через полную ширину отражения на половине высоты 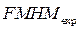 как
как 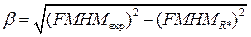 .Если вторые моменты и полная ширина выражены в одинаковых единицах (все в углах
.Если вторые моменты и полная ширина выражены в одинаковых единицах (все в углах 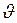 или все в углах 2
или все в углах 2 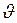 ), то
), то 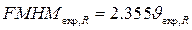 и уширение отражения (hkl) равно
и уширение отражения (hkl) равно
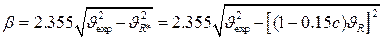 . (4.17)
. (4.17)
Как уже отмечалось, уширения, вызванные малым размером зёрен, деформациями и негомогенностью, пропорциональны sec 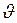 , tg
, tg 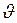 и (sin
и (sin 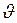 )2/cos
)2/cos 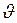 , соответственно, поэтому благодаря разной угловой зависимости можно разделить три разных вида уширения. При этом следует иметь в виду, что размер областей когерентного рассеяния, определяемый из размерного уширения, может соответствовать размеру индивидуальных частиц (кристаллитов), но может также отражать субдоменную структуру и характеризовать среднее расстояние между дефектами упаковки или эффективный размер мозаичных блоков и т. д. Кроме того, нужно учитывать, что форма дифракционного отражения зависит не только от размера, но и от формы наночастиц. В неоднофазных наноматериалах заметное искажение формы наблюдаемых дифракционных линий может быть следствием суперпозиции дифракционных отражений нескольких фаз.
, соответственно, поэтому благодаря разной угловой зависимости можно разделить три разных вида уширения. При этом следует иметь в виду, что размер областей когерентного рассеяния, определяемый из размерного уширения, может соответствовать размеру индивидуальных частиц (кристаллитов), но может также отражать субдоменную структуру и характеризовать среднее расстояние между дефектами упаковки или эффективный размер мозаичных блоков и т. д. Кроме того, нужно учитывать, что форма дифракционного отражения зависит не только от размера, но и от формы наночастиц. В неоднофазных наноматериалах заметное искажение формы наблюдаемых дифракционных линий может быть следствием суперпозиции дифракционных отражений нескольких фаз.
Рассмотрим, как можно разделить уширение, обусловленное несколькими разными факторами, на примере наноструктурированных карбидных твёрдых растворов системы Zr C – Nb C. При рентгеновском исследовании этих твёрдых растворов было обнаружено, что дифракционные отражения на рентгенограммах образцов (ZrС)0.46(NbС)0,54 сильно уширены. Известно, что эти твёрдые растворы имеют склонность к распаду в твёрдом состоянии, однако по рентгеновским данным образцы были однофазны. Для выяснения причины уширения отражений (негомогенность, малый размер зёрен или деформации) был выполнен количественный анализ профиля дифракционных отражений с использованием псевдо-функции Фойгта (2.19). Проведенный анализ показал, что ширина всех дифракционных отражений существенно превышает ширину функции разрешения дифрактометра.
Уширение 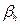 , обусловленное негомогенностью Δх твёрдого раствора А1-xВx, состав которого меняется в интервале х ± Δх, пропорционально (sin
, обусловленное негомогенностью Δх твёрдого раствора А1-xВx, состав которого меняется в интервале х ± Δх, пропорционально (sin 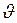 )2/cos
)2/cos 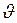 :
:
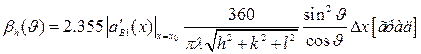 (2.28)
(2.28)
или измеренное в радианах, равно
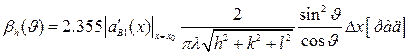 (2.29)
(2.29)
где 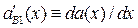 — производная от концентрационной зависимости периода решётки твёрдого раствора по составу х.
— производная от концентрационной зависимости периода решётки твёрдого раствора по составу х.
Уширение 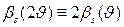 , обусловленное малым размером частицы (кристаллита, домена), связано со средним размером частицы
, обусловленное малым размером частицы (кристаллита, домена), связано со средним размером частицы 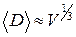 (V — объём частицы) формулой, которую запишем в виде
(V — объём частицы) формулой, которую запишем в виде
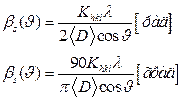 (2.30)
(2.30)
В кубической кристаллической решётке кристаллиты имеют размеры одного порядка в трех перпендикулярных направлениях. В этом случае для кристаллов с кубической симметрией коэффициент 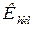 отражений с различными кристаллографическими индексами Миллера (hkl) кубической кристаллической решётки, можно вычислить по формуле
отражений с различными кристаллографическими индексами Миллера (hkl) кубической кристаллической решётки, можно вычислить по формуле
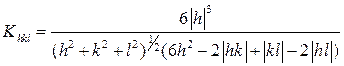 (2.31)
(2.31)
Деформационные искажения и обусловленные ими неоднородные смещения атомов из узлов решётки могут возникать при хаотическом размещении дислокаций в объёме образца. В этом случае смещения атомов определяются суперпозицией смещений от каждой дислокации, что можно рассматривать как локальное изменение межплоскостных расстояний. Иначе говоря, расстояние между плоскостями непрерывно меняется от (d0 -Δd) до (d0 +Δd) (d0 и Δd — межплоскостное расстояние в идеальном кристалле и среднее по величине изменение расстояния между плоскостями (hkl) в объёме V кристалла, соответственно). В этом случае величина ε = Δd / d0 есть микродеформация решётки, которая характеризует усреднённую по кристаллу величину однородной деформации. Дифракционный максимум от областей кристалла с измененным межплоскостным расстоянием возникает под углом 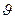 , несколько отличающимся от угла
, несколько отличающимся от угла 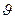 о для идеального кристалла, и в результате этого происходит уширение отражения. Формулу для уширения линии, связанного с микродеформацией решётки, легко вывести, продифференцировав уравнение Вульфа-Брегга:
о для идеального кристалла, и в результате этого происходит уширение отражения. Формулу для уширения линии, связанного с микродеформацией решётки, легко вывести, продифференцировав уравнение Вульфа-Брегга: 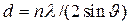 ;
; 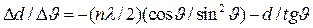 .Уширение линии в одну сторону от максимума линии, соответствующего межплоскостному расстоянию d, при изменении межплоскостного расстояния на + Δd равно
.Уширение линии в одну сторону от максимума линии, соответствующего межплоскостному расстоянию d, при изменении межплоскостного расстояния на + Δd равно 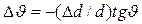 , а при изменении на - Δd, равно
, а при изменении на - Δd, равно 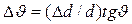 . Общее уширение линии равно сумме этих уширений и по углу
. Общее уширение линии равно сумме этих уширений и по углу 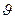 составляет
составляет
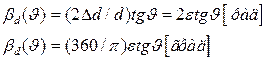 (2.32)
(2.32)
С учетом 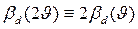 деформационное уширение по 2υ составляет
деформационное уширение по 2υ составляет
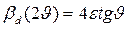 (2.33)
(2.33)
Заметим, что в (2.28)-(2.30) и (2.33) уширение 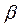 определяется в градусах
определяется в градусах 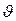 , а не 2
, а не 2 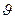 .
.
Полная ширина FWHMехр и второй момент 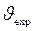 каждого экспериментального дифракционного отражения твёрдого раствора (ZrС)0.46(NbС)0,54 найдены аппроксимацией отражений функцией (2.19) с А = 1. Уширение
каждого экспериментального дифракционного отражения твёрдого раствора (ZrС)0.46(NbС)0,54 найдены аппроксимацией отражений функцией (2.19) с А = 1. Уширение 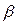 отражений (hkl) определяли по формуле (2.27). Угловую зависимость второго момента
отражений (hkl) определяли по формуле (2.27). Угловую зависимость второго момента 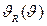 (рис. 6 а) функции разрешения рентгеновского дифрактометра определяли в специальных экспериментах на отожжённых крупнозернистых соединениях, не имеющих области гомогенности (большой размер зёрен, отсутствие деформационных искажений и однородность состава образцов исключали уширение отражений): монокристалле гексагонального карбида кремния 6Н-SiC и на стехиометрическом карбиде вольфрама WС. Сопоставление найденных величин
(рис. 6 а) функции разрешения рентгеновского дифрактометра определяли в специальных экспериментах на отожжённых крупнозернистых соединениях, не имеющих области гомогенности (большой размер зёрен, отсутствие деформационных искажений и однородность состава образцов исключали уширение отражений): монокристалле гексагонального карбида кремния 6Н-SiC и на стехиометрическом карбиде вольфрама WС. Сопоставление найденных величин 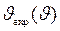 с функцией разрешения
с функцией разрешения 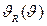 позволило найти угловую зависимость
позволило найти угловую зависимость 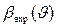 экспериментального уширения отражений. Численный анализ показал, что наиболее близки к линейным зависимости, характерные для уширений, связанных с негомогенностью и с размером кристаллитов, тогда как деформационное уширение (а значит и хаотически расположенные дислокации) в исследуемых образцах отсутствует.
экспериментального уширения отражений. Численный анализ показал, что наиболее близки к линейным зависимости, характерные для уширений, связанных с негомогенностью и с размером кристаллитов, тогда как деформационное уширение (а значит и хаотически расположенные дислокации) в исследуемых образцах отсутствует.
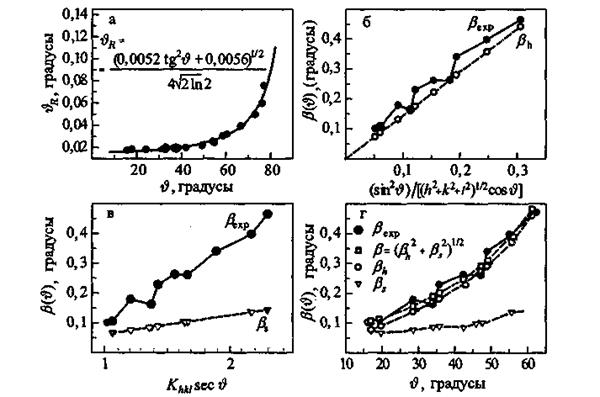 |
Рис 9. Второй момент 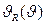 функции разрешения а — дифрактометра и выделение вкладов в уширение дифракционных отражений твёрдого раствора (ZrС)0.46(NbС)0,54 б — зависимость экспериментального уширения функции разрешения а — дифрактометра и выделение вкладов в уширение дифракционных отражений твёрдого раствора (ZrС)0.46(NbС)0,54 б — зависимость экспериментального уширения 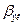 от от 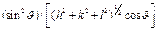 и выделенный вклад негомогенного уширения и выделенный вклад негомогенного уширения 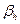 ; в — зависимость экспериментального уширения ; в — зависимость экспериментального уширения 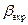 от от 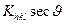 и выделенный вклад размерного уширения и выделенный вклад размерного уширения 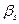 ; г — зависимости экспериментального ; г — зависимости экспериментального 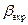 , размерного , размерного 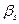 и негомогенного и негомогенного 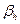 , уширений от угла дифракции , уширений от угла дифракции 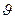 и аппроксимация экспериментального уширения суперпозицией уширений и аппроксимация экспериментального уширения суперпозицией уширений 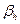 и и 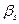 в виде в виде 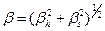 |
Таким образом можно считать, что наблюдаемое уширение дифракционных отражений является суперпозицией только двух факторов 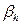 и
и 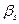 . С учётом этого на рис. 2.12 построены зависимости экспериментально наблюдаемого уширения
. С учётом этого на рис. 2.12 построены зависимости экспериментально наблюдаемого уширения 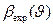 дифракционных отражений образца (ZrС)0.46(NbС)0,54 от
дифракционных отражений образца (ZrС)0.46(NbС)0,54 от 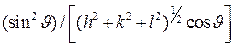 и
и 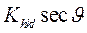 . Поскольку наблюдаемое уширение является результатом двух независимых механизмов, то его можно найти как свёртку двух функций: первая из них соответствует уширению, обусловленному негомогенностью, вторая соответствует уширению, вызванному малым размером зёрен. В этом случае величину суммарного уширения можно оценить по формуле
. Поскольку наблюдаемое уширение является результатом двух независимых механизмов, то его можно найти как свёртку двух функций: первая из них соответствует уширению, обусловленному негомогенностью, вторая соответствует уширению, вызванному малым размером зёрен. В этом случае величину суммарного уширения можно оценить по формуле
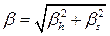 (2.34)
(2.34)
Расчет показал, что выделенные вклады уширения 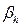 , обусловленного негомогенностью, и размерного уширения
, обусловленного негомогенностью, и размерного уширения 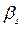 являются линейными функциями от
являются линейными функциями от 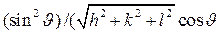 и
и 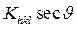 соответственно (рис. 6 а и 6 б), что подтверждает наличие именно этих двух вкладов.
соответственно (рис. 6 а и 6 б), что подтверждает наличие именно этих двух вкладов.
[1]. Дзюба С.А. Основы магнитного резонанса. Ч. I: Спектры магнитного резонанса: Учеб. пособие / Новосиб. ун-т. Новосибирск, 1994. – 108 с.
[2]. Guinier A., Fournet G. Small-angle scattering of x-rays. New York-London: J. Wiley and Sons. Chapman and Hall Ltd. 1955.
[3]. Игнатенко П. И., Иваницын Н. П. Рентгенография реальных кристаллов. - Донецк: ДГУ, 2000. – 328 с.
[4]. Русаков, А. А. Рентгенография металлов - М.: Атомиздат, 1977. - 479 с.
[5]. Гусев А.И. Наноматериалы, наноструктуры, нанотехнологии. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
 2015-07-21
2015-07-21 4099
4099







