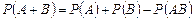 ;
;
б) в частности, если события  и
и  несовместны то
несовместны то
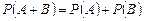 ;
;
в) для трёх событий
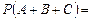
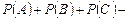
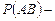
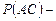
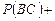
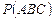 ;
;
г) для 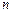 событий
событий
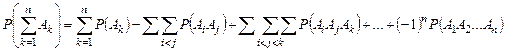 .
.
д) в частности, если события 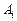 ,
, 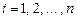 попарно несовместны, то
попарно несовместны, то
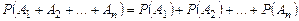 ;
;
е) если же события 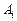 ,
, 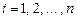 независимы в совокупности, то
независимы в совокупности, то
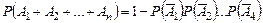 . (1.10.1)
. (1.10.1)
Вероятность произведения событий:
а) для двух событий
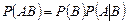 ;
;
б) в частности, если события  и
и  независимы, то
независимы, то
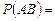
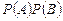 .
.
г) для 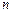 событий
событий
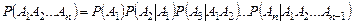 .
.
д) в частности, если события 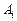 ,
, 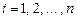 независимы в совокупности, то
независимы в совокупности, то
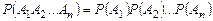 . (1.10.2)
. (1.10.2)
Формулы полной вероятности и Байеса:
а) 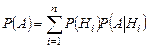 ;
;
б) 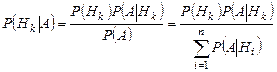 .
.
Формула Бернулли:
вероятность появления ровно 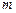 успехов в серии из
успехов в серии из 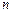 испытаний по схеме Бернулли с вероятностью успеха
испытаний по схеме Бернулли с вероятностью успеха 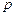 равна
равна
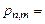
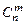
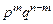 , где
, где 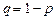 .
.
Пример 1.10.2.
Убедимся в справедливости равенства (1.10.1).
◄Используя правило де Моргана (1.2.5) 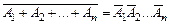 с учётом (1.10.2) имеем:
с учётом (1.10.2) имеем:
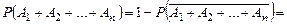
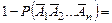
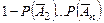 .►
.►
 2015-07-21
2015-07-21 418
418








