Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции 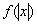получается из графика функции 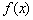следующим образом: при 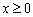график функции 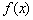сохраняется, а при 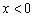«сохранённая часть» отображается симметрично относительно оси .

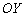Пример 22

Построить график функции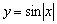

И снова вечная картина:

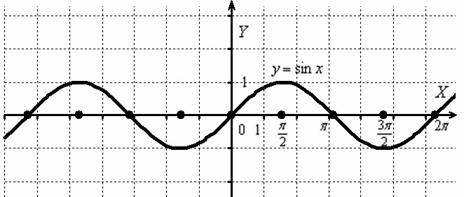
Согласно правилу, при 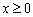график сохраняется:

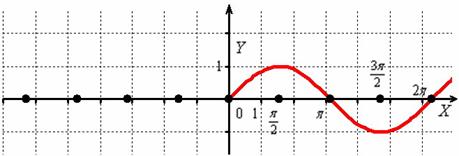
И сохранившаяся часть отображается симметрично относительно оси 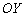в левую полуплоскость:

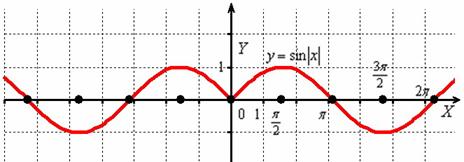
Действительно, функция 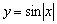– чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на 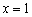и 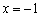. А какая разница? Модуль всё равно уничтожит знак «минус»: 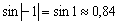, то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: 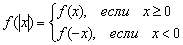. В данном случае:

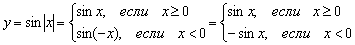
То есть, правая волна графика 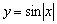задаётся функцией 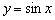, а левая волна – функцией 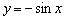(см. Пример 13).

Пример 23

Построить график функции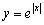

Аналогично, ветвь «обычной» экспоненты 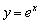правой полуплоскости отображаем симметрично относительно оси 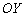в левую полуплоскость:

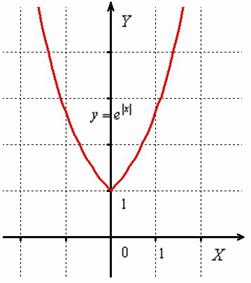
Распишем функцию в кусочном виде: 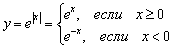, то есть правая ветвь задаётся графиком функции 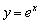, а левая ветвь графиком .

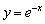Модуль не имеет смысл «навешивать» на аргумент чётной функции: 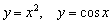и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции 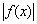получается из графика функции 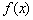следующим образом: часть графика 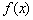, лежащая НАД осью 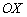сохраняется, а часть графика 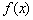, лежащая ПОД осью 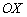отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-ой позиции, но факт остаётся фактом =)

Пример 24

Построить график функции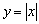

Сначала начертим прямую, известную широкому кругу лиц:

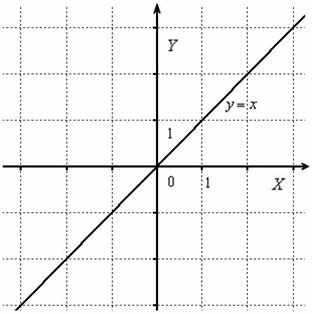
Часть графика, которая ВЫШЕ оси 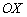, остаётся неизменной, а часть графика, которая НИЖЕ оси 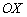– отображается симметрично в верхнюю полуплоскость:

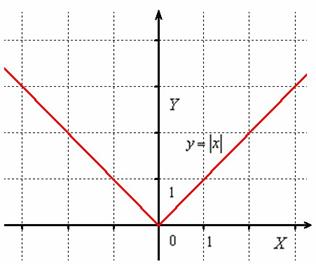
Модуль функции также раскрывается аналитически в кусочном виде:

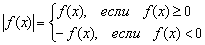
Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: 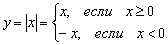, действительно, правый луч задаётся уравнением 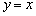, а левый луч – уравнением .

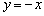Кстати, 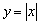– редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: 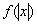, так и к самой функции: 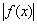. Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции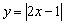

Сначала изобразим график линейной функции :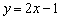

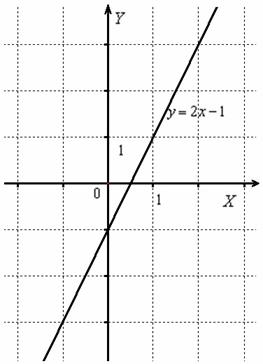
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси 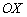в верхнюю полуплоскость:

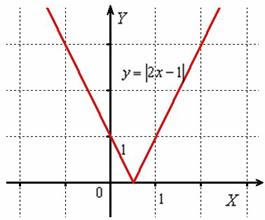
Согласно формуле 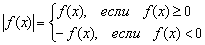, распишем функцию аналитически в кусочном виде: .

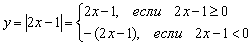Или, упрощая оба этажа: 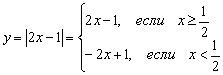, то есть правый луч задаётся функцией 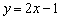, а левый луч – функцией 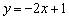. Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: 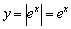. Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

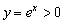Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .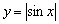

Изобразим сами знаете что =)

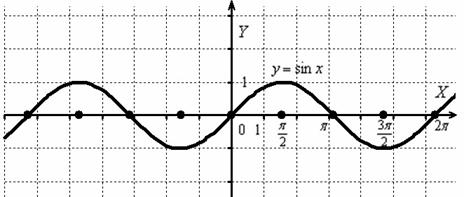
И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :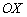

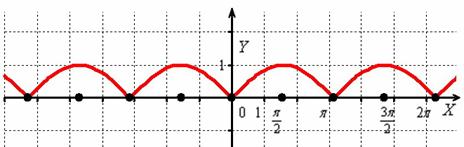
Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

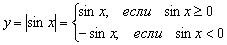
Решив два простейших школьных неравенства 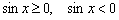, получаем:
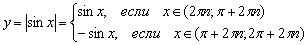, где 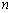– любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Непрерывность функции. Точки разрыва.
Как исследовать функцию на непрерывность?

Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!

На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.

Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции. Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций. Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!