Цель: формирование умения находить промежутки выпуклости, вогнутости графика функции и его точки перегиба.
Задание для самостоятельной внеаудиторной работы:
& 19.1.Выучите определения вогнутого и выпуклого на интервале графика функции, точки перегиба. Запомните критерий выпуклости (вогнутости) графика функции.
& 19.2.Выясните, в чем заключается достаточное условие существования точек перегиба. Детально изучите и постарайтесь освоить алгоритм, позволяющий находить промежутки выпуклости (вогнутости) графика функции и точки перегиба.
?19.3. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции:
а) 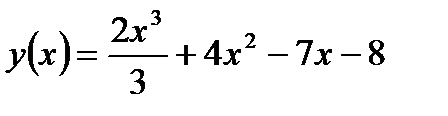 ; б)
; б) 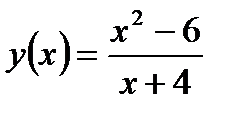 ; в)
; в) 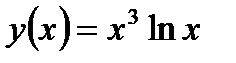 .
.
¶ 19.4. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 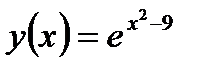 .
.
¶ 19.5. Определите, при каком значении а график функции 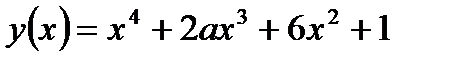 будет вогнутым на области определения функции.
будет вогнутым на области определения функции. 

Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
График функции 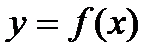 называется вогнутым на интервале
называется вогнутым на интервале 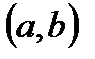 , если он расположен выше любой касательной к графику функции на данном интервале.
, если он расположен выше любой касательной к графику функции на данном интервале.
График функции 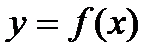 называется выпуклым на интервале
называется выпуклым на интервале 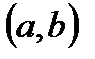 , если он расположен ниже любой касательной к графику функции на данном интервале.
, если он расположен ниже любой касательной к графику функции на данном интервале.
Точка графика непрерывной функции, в которой меняется характер выпуклости, называется точкой перегиба.
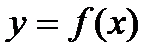 |
| у |
| х2 |
| у1 |
| х |
| 0 |
| Рис. 1. |
| х1 |
| у2 |
Так, график функции на рис.1. является выпуклым на промежутках (- 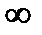 ; х 1) и (х 2; +
; х 1) и (х 2; + 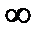 ); вогнутым на (х 1; х 2). График функции имеет две точки перегиба: (х 1; у 1) и (х 2; у 2).
); вогнутым на (х 1; х 2). График функции имеет две точки перегиба: (х 1; у 1) и (х 2; у 2).
Критерий выпуклости-вогнутости функции: если функция 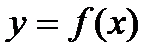 имеет положительную вторую производную, то график функции на интервале
имеет положительную вторую производную, то график функции на интервале 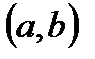 вогнутый;
вогнутый;
если функция 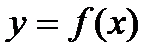 имеет отрицательную вторую производную, то график функции на интервале
имеет отрицательную вторую производную, то график функции на интервале 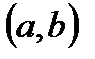 выпуклый.
выпуклый.
Критерий выпуклости-вогнутости функции удобно представляется в виде схемы:
| f(x) вогнутая | 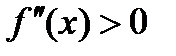 | |
| f(x) выпуклая | 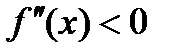 |
Таким образом, исследовать функцию на выпуклость-вогнутость означает найти те интервалы области определения, в которых вторая производная сохраняет свой знак.
Критическими точками функции второго р ода называются те точки, в которых вторая производная равна нулю или не существует. Только критические точки могут быть точками перегиба. Для их нахождения используется следующая теорема:
Теорема (достаточное условие существования точек перегиба). Если вторая производная 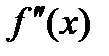 при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.
при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.
При исследовании функции 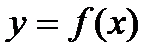 на выпуклость-вогнутость и точки перегиба удобно использовать следующий алгоритм:
на выпуклость-вогнутость и точки перегиба удобно использовать следующий алгоритм:
- Найдите область определения функции.
- Найдите первую производную функции
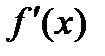 .
. - Найдите вторую производную функции
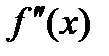 .
. - Определите критические точки второго рода (
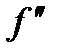 (xo) =0 или
(xo) =0 или 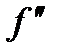 (xo) не существует).
(xo) не существует). - На числовой оси отметьте критические точки второго рода и определите знаки второй производной на каждом из получившихся интервалов.
- Найдите интервалы выпуклости-вогнутости графика функции, используя соответствующие критерии; выпишите абсциссы точек перегиба (если они есть) и найдите значение функции в этих точках.
Пример 1. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 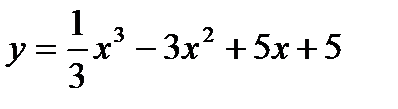 .
.
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции: 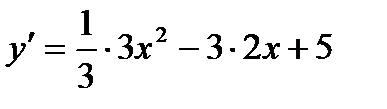 =
= 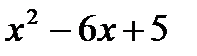 .
.
3. Найдем вторую производную функции: 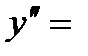
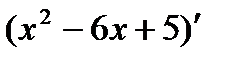 =2 х -6.
=2 х -6.
4. Определим критические точки второго рода (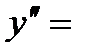 0): 2 х -6= 0
0): 2 х -6= 0 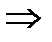 х =3.
х =3.
5. На числовой оси отметим критическую точку х =3. Она разбивает область определения функции на два интервала (-∞;3) и (3;+∞). Расставим знаки второй производной функции 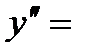 2 х -6 на каждом из полученных интервалов:
2 х -6 на каждом из полученных интервалов:
при х =0  (-∞;3)
(-∞;3) 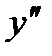 (0)=-6<0;
(0)=-6<0;
при х =4  (3;+∞)
(3;+∞) 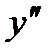 (4)= 2∙4-6=2>0.
(4)= 2∙4-6=2>0.
| т. перегиба |
| х |
| + |
 |
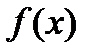 |
| вып. |
| вогн. |
6. Согласно критерию выпуклости-вогнутости график функции 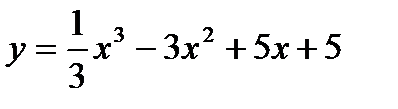 выпуклый при х
выпуклый при х  (-∞;3), вогнутый при х
(-∞;3), вогнутый при х  (3;+ ∞).
(3;+ ∞).
Значение х =3 – абсцисса точки перегиба. Вычислим значение функции при х =3:
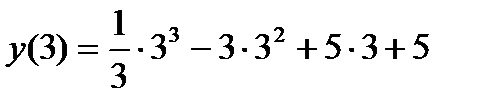 =
= 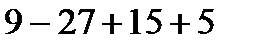 =2. Итак, точка с координатами (3;2) – точка перегиба.
=2. Итак, точка с координатами (3;2) – точка перегиба.
Ответ: график функции 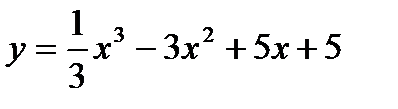 выпуклый при х
выпуклый при х  (-∞;3),
(-∞;3),
вогнутый при х  (3;+ ∞); (3;2) – точка перегиба.
(3;+ ∞); (3;2) – точка перегиба.
Пример 2. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 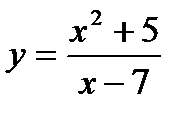 .
.
Решение. 1. Данная функция определена в том случае, когда знаменатель отличен от нуля: х -7≠0 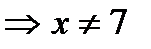 .
.
2. Найдем первую производную функции:
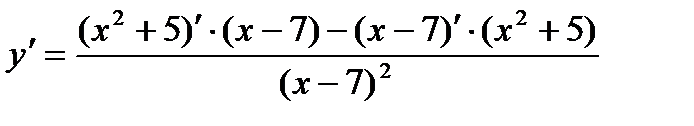 =
= 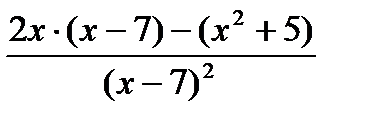 =
= 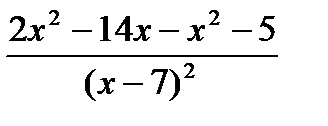 =
=
= 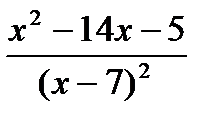 .
.
3. Найдем вторую производную функции: 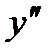 =
= 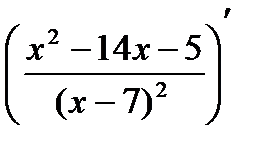 =
=
= 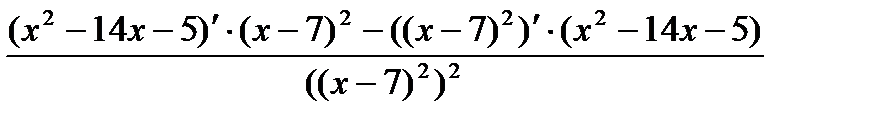 =
=
= 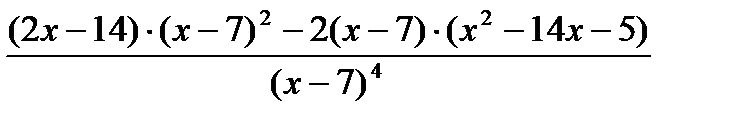 .
.
Вынесем в числителе 2∙(х -7) за скобки:
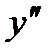 =
= 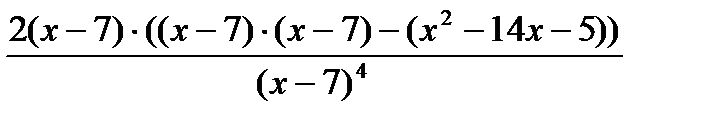 =2∙
=2∙ 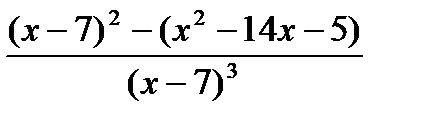 =
=
= 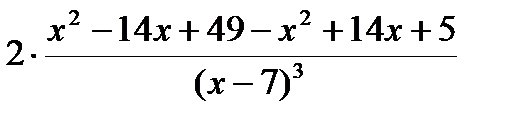 =
= 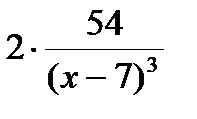 =
= 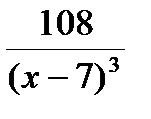 .
.
4. Определим критические точки второго рода: 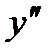 не может быть равна нулю, поскольку числитель дроби 108≠0.
не может быть равна нулю, поскольку числитель дроби 108≠0.
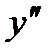 не существует, если (х -7)3=0
не существует, если (х -7)3=0 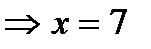 - критическая точка второго рода.
- критическая точка второго рода.
5. На числовой оси отметим критическую точку х =7 выколотой точкой, поскольку в этой точке функция 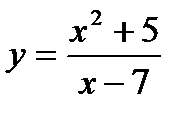 не определена. Эта точка разбивает область определения функции на два интервала (-∞;7) и (7;+∞). Расставим знаки второй производной функции
не определена. Эта точка разбивает область определения функции на два интервала (-∞;7) и (7;+∞). Расставим знаки второй производной функции 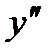 =
= 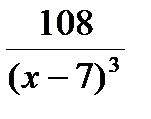 на каждом из полученных интервалов:
на каждом из полученных интервалов:
при х =6  (-∞;7)
(-∞;7) 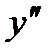 (6)=
(6)= 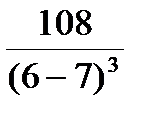 <0;
<0;
при х =8  (7;+∞)
(7;+∞) 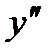 (8)=
(8)= 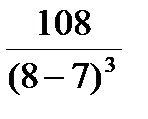 >0.
>0.
| вогн. |
| х |
| + |
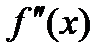 |
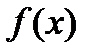 |
| вып. |
6. Согласно критерию выпуклости-вогнутости график функции 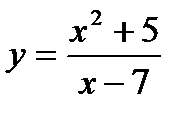 является выпуклым при х
является выпуклым при х  (-∞;7), вогнутым при х
(-∞;7), вогнутым при х  (7;+ ∞).
(7;+ ∞).
Точка с абсциссой х =7 не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
Ответ: график функции 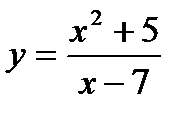 выпуклый при х
выпуклый при х  (-∞;7), вогнутый при х
(-∞;7), вогнутый при х  (7;+ ∞).
(7;+ ∞).
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.8, стр. 141 – 144.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 40, стр. 227-231.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §7, стр. 274– 278.
 2015-04-01
2015-04-01 3626
3626
