Основные понятия. Понятие функции является одним из главных понятий математики

Понятие функции является одним из главных понятий математики. С этим понятием часто встречаемся в природе, изучая различные процессы и явления.

Пусть 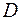– некоторое множество действительных чисел. Если каждому числу 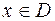– поставлено в соответствие по какому-то правилу или закону 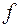единственное действительное число , то говорят, что на множестве 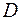задана функция одного переменного и обозначается: 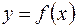. Число 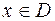называется аргументом функции, – значением функции, множество 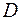– областью определения функции, множество всех значений , которые соответствуют числам множества 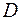– областью значений функции – . (См. рис. 28)

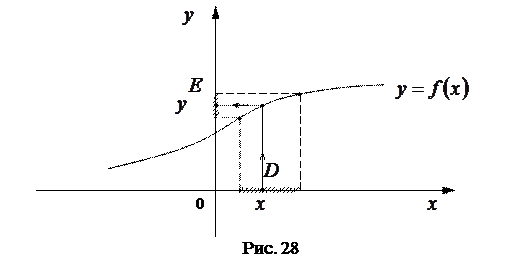
Графиком 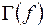функции 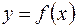называется множество всех точек 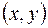плоскости 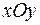таких, что 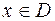, а 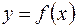, то есть

.

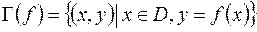Далее будем задавать функцию одного переменного аналитически, то есть с помощью формулы. В этом случае под областью определения 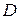функции понимают множество всех тех значений 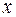, для которых данная формула имеет смысл.

Пример. Формула 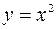задает функцию одного переменного 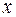. Поскольку данная формула имеет смысл при всех действительных значениях переменной 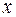, то область определения 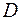данной функции есть множество всех действительных чисел 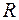, то есть 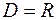. Так как квадрат действительного числа – число неотрицательное, то множество значений данной функции 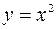есть множество всех неотрицательных чисел, то есть 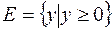. Графиком функции 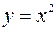является парабола в плоскости 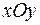с вершиной в точке 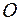, ветви которой направлены в положительном направлении оси 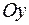. (См. рис. 29)

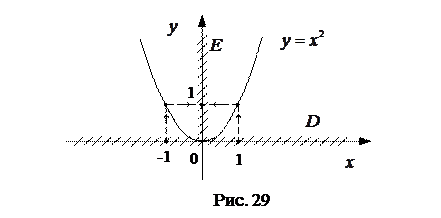
Пусть задана функция 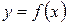, , 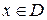такая, что для 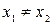, , 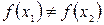то есть для любого 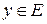найдется единственное 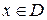такое, что 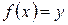или 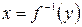. Тем самым определена функция 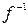, называемая функцией, обратной к функции 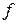. (См. рис. 30)

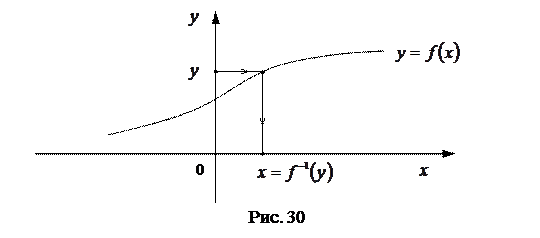
Покажем как строим график обратной функции. Если для обратной функции обозначить аргумент через 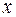, а функцию через , то графики функций и 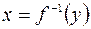совпадают. Разница состоит лишь в том, что для функции ось 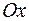– ось абсцисс, а ось 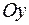– ось ординат, а для функции 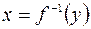роль осей меняется.

Если же обозначить аргумент обратной функции через 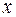, а значение функции через , то получается иной график. Именно, нужно перевести друг в друга ос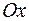и и 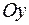. Это делается с помощью отражения всей плоскости 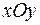относительно биссектрисы первого координатного угла, то есть прямой 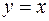. При этом отражении график функции переходит в график обратной функции .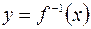

Итак, график обратной функции симметричен графику заданной функции относительно прямой 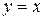. (См. рис.31)

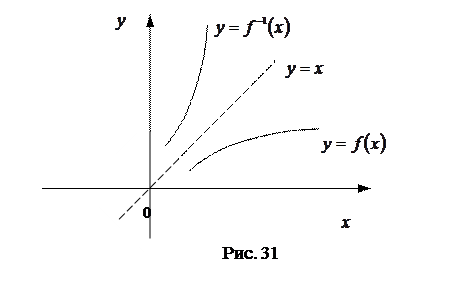
Пример. Функция 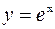является обратной функцией к функции 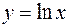. (См. рис. 32)