2015-07-21
353
Интегрирования
Свойство 1. Производная (дифференциал) неопределенного интеграла равна подынтегральной функции: d/dx(∫ f(x)dx)=f(x)
Свойство 2. Постоянный множитель можно выносить за знак интеграла: ∫ c*f(x)dx=c*∫ f(x)dx
Свойство 3. Интеграл от алгебраической суммы равен алгебраической сумме интегралов от каждого слагаемого в отдельности:
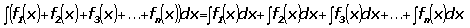
Формулы интегрирования
Из каждой формулы дифференцирования, если ее обратить, получается соответствующая формула интегрирования. В результате получают основные табличные интегралы:
1. 
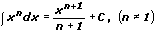
2. 
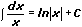
3. 
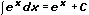
4. 
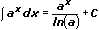
5. 
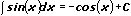
6. 
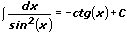
7. 
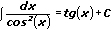
8. 
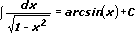
9. 
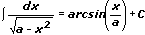
10. 
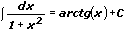
11. 
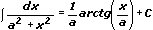
12. 
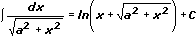
13. 
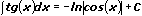
14. 
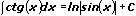
15. 
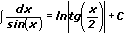
16. 
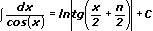
17.
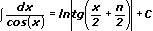
18. 
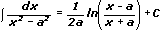
21. Основные приемы интегрирования неопределенного интеграла:
Метод непосредственного интегрирования, метод интегрирования через вспомогательную переменную (метод подстановки),
