1. Задача Коши для одномерного волнового уравнения на всей прямой. Формула Даламбера.
2. Теорема сложения вероятностей (с доказательством). Вероятность противоположного события.
3. Найти решение смешанной задачи
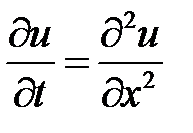 ,
, 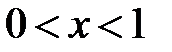 ,
,
ГУ: 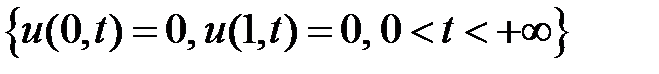 ; НУ:
; НУ: 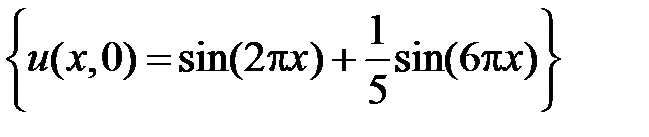 .
.
4. В хлопке 75% длинных волокон. Какова вероятность того, что среди взятых наудачу трёх волокон окажутся 2 длинных волокна?
1. Задача Коши для одномерного волнового уравнения на всей прямой имеет вид:
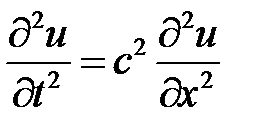 ,
, 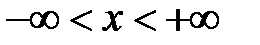 ,
, 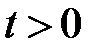 ,
,
начальные условия: 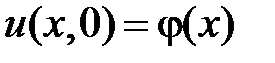 ,
, 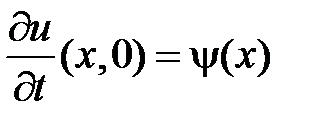 .
.
Решение задачи будем искать в виде суммы прямой и обратной бегущих волн:
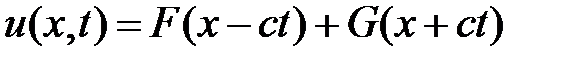 .
.
Воспользуемся для нахождения функций 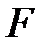 и
и 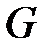 начальными условиями:
начальными условиями:
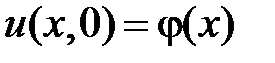 :
: 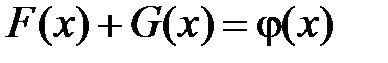 ,
,
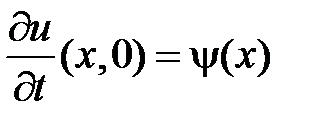 :
: 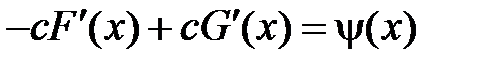 .
.
Интегрируя уравнение 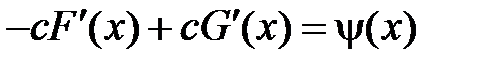 в пределах от
в пределах от 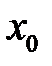 до
до 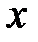 , получим
, получим
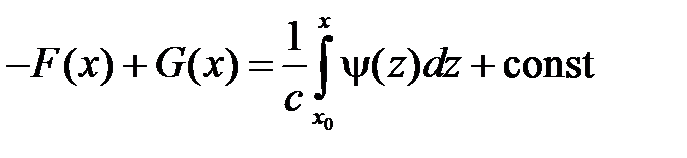 .
.
Тогда из системы
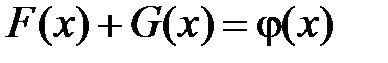 ,
, 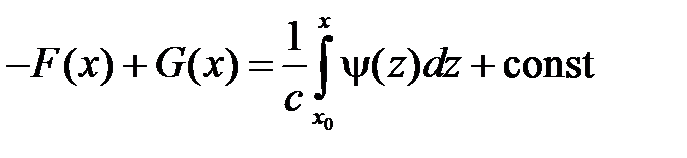 ,
,
находим
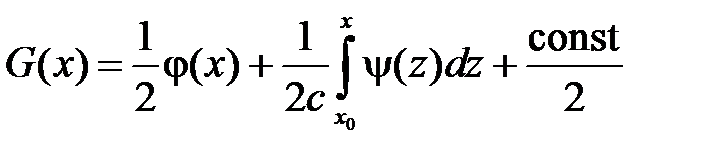 ,
,
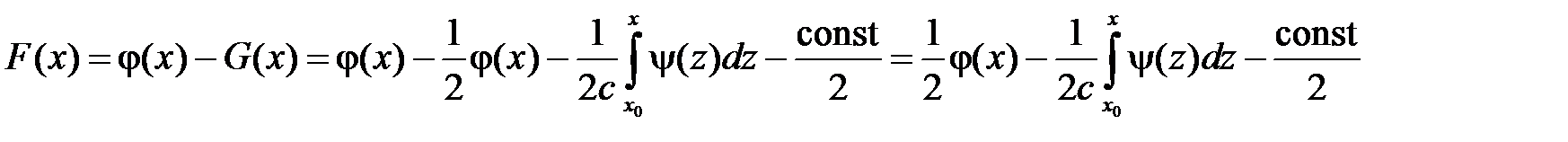 .
.
Значит,
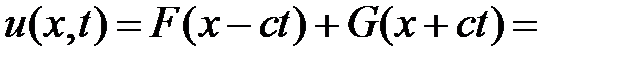
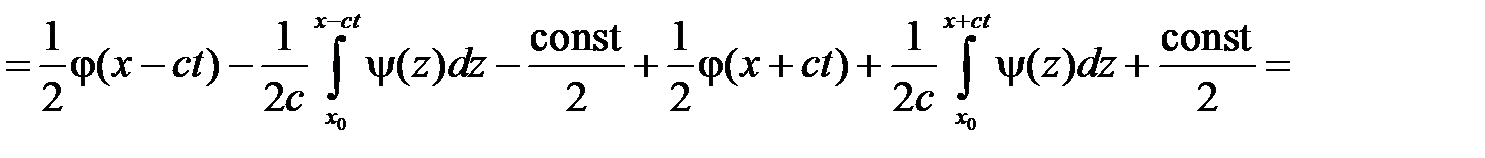
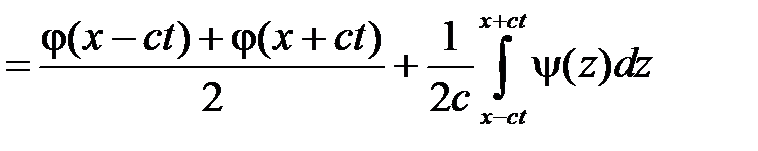 .
.
Итак, решение задачи Коши для одномерного волнового уравнения на всей прямой имеет вид
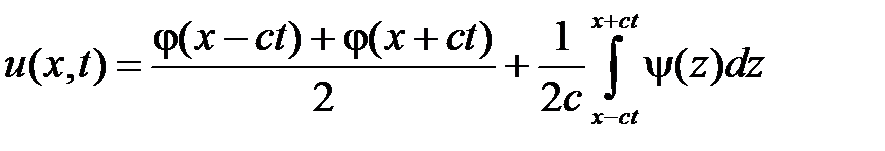 .
.
Это формула Даламбера.
2. Теорема сложения вероятностей. Если события 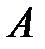 и
и 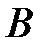 совместны, то
совместны, то
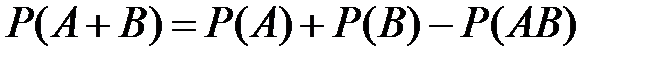 .
.
Доказательство. Пусть 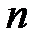 – числе всех равновозможных исходов испытания, в результате которого могут появиться события
– числе всех равновозможных исходов испытания, в результате которого могут появиться события 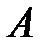 и
и 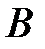 . Пусть
. Пусть 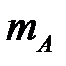 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 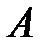 ,
, 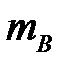 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 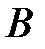 ,
, 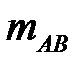 – число тех исходов, которые благоприятствуют произведению событий
– число тех исходов, которые благоприятствуют произведению событий 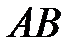 . Тогда событию
. Тогда событию 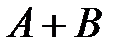 благоприятствуют исходы числом
благоприятствуют исходы числом 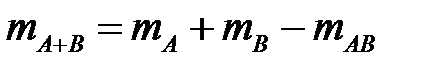 . Значит, по формуле классической вероятности
. Значит, по формуле классической вероятности
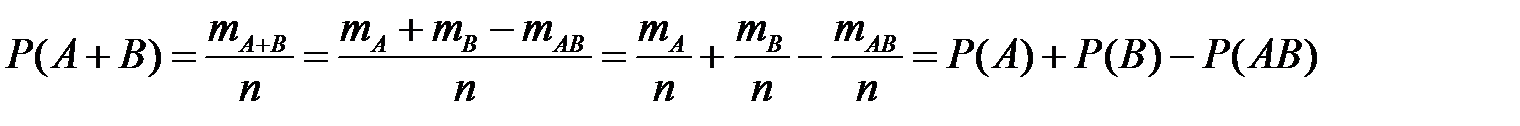 .
.
Следствие. Если события 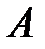 и
и 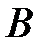 несовместны, то
несовместны, то 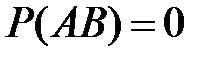 и
и
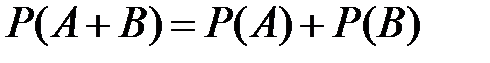 .
.
Для трех событий 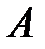 ,
, 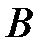 и
и  теорема сложения имеет вид
теорема сложения имеет вид
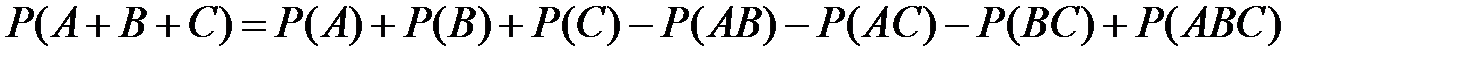 .
.
Для 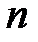 событий теорема сложения имеет вид
событий теорема сложения имеет вид
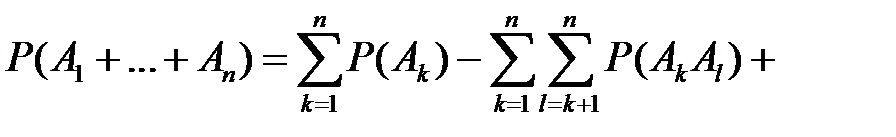
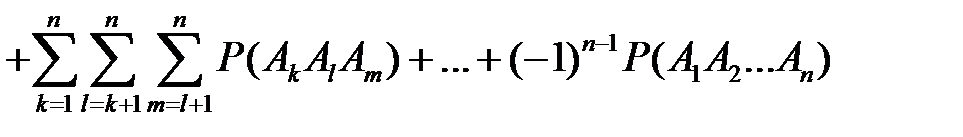 .
.
Противоположные события 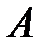 и
и 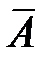 несовместны и в сумме дают достоверное событие, поэтому
несовместны и в сумме дают достоверное событие, поэтому
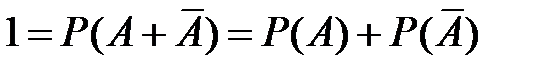 ,
,
откуда получаем формулу для вероятности противоположного события
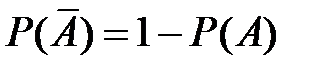 .
.
3. Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 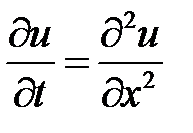 будем искать в виде
будем искать в виде 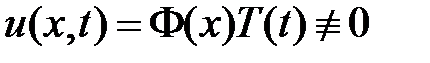 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
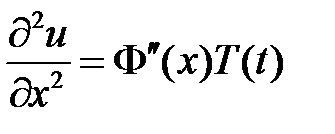 ,
, 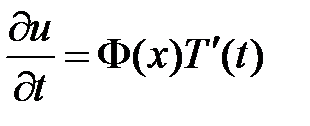 ,
,
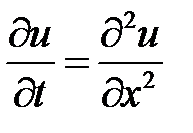 :
: 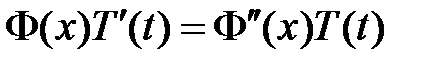 ,
,
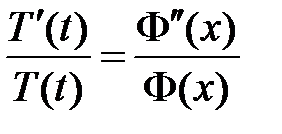 ,
, 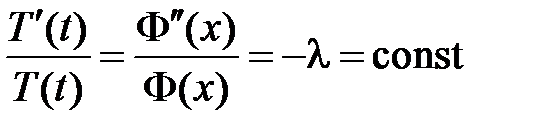 ,
, 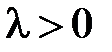 .
.
Тогда функции 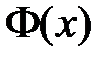 и
и 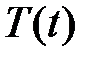 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 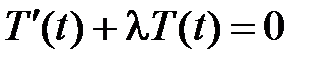 .
.
Из граничных условий 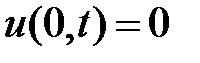 ,
, 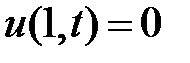 получаем краевые условия для функции
получаем краевые условия для функции 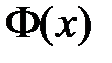 :
: 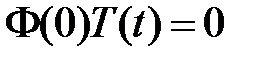 ,
, 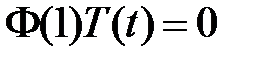 , значит,
, значит, 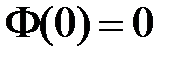 ,
, 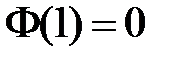 . Таким образом, для определения
. Таким образом, для определения 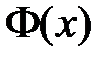 и
и 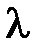 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

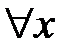 :
: 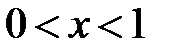 ,
,
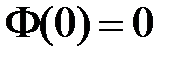 ,
, 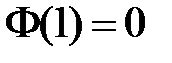 .
.
Поскольку 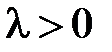 (при
(при 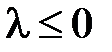 задача имеет только тривиальные решения), то общее решение уравнения
задача имеет только тривиальные решения), то общее решение уравнения  имеет вид
имеет вид
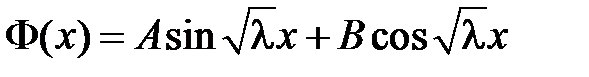 .
.
Из краевого условия 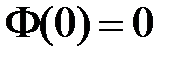 получаем:
получаем: 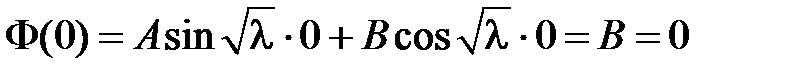 , т.е.
, т.е. 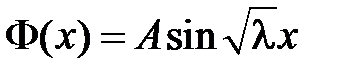 .
.
Из краевого условия 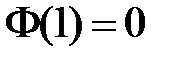 получаем:
получаем: 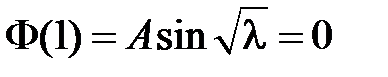 . Поскольку
. Поскольку 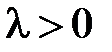 и
и 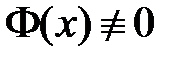 , то
, то 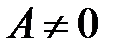 и равенство
и равенство 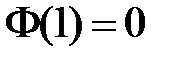 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 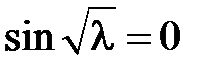 , откуда получаем
, откуда получаем 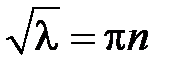 ,
,  , т.е.
, т.е. 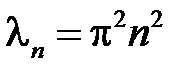 ,
,  . Тогда получим
. Тогда получим 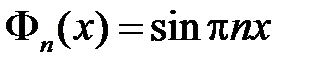 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные функции 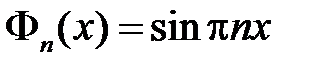 ,
,  .
.
Теперь при каждом 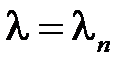 решаем уравнение для
решаем уравнение для 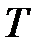 :
:
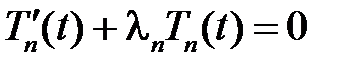 ,
,  .
.
Общее решение этого уравнения имеет вид
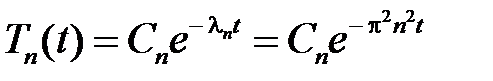 .
.
Тогда
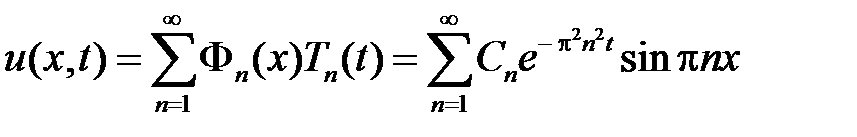 .
.
Для нахождения коэффициентов 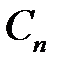 ,
,  , воспользуемся начальным условием
, воспользуемся начальным условием 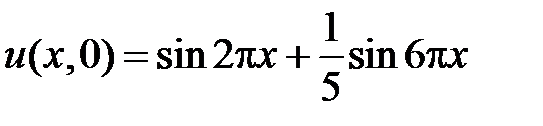 .
.
Начальное условие 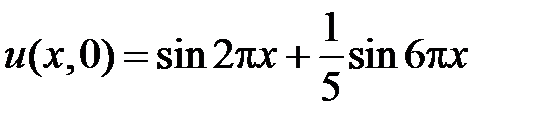 дает
дает
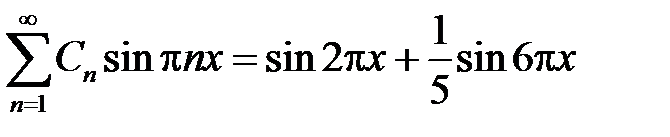 ,
,
откуда
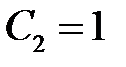 ,
, 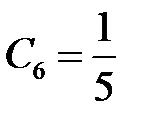 ,
, 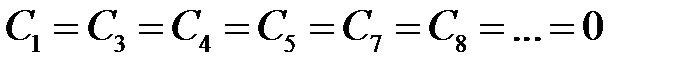 .
.
Тогда решение задачи есть
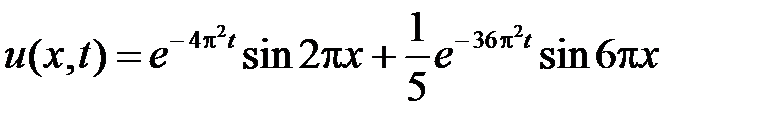 .
.
4. Мы имеем дело с последовательностью независимых испытаний по схеме Бернулли, где событие «успех» – появление при выборе длинного волокна. По условию вероятность «успеха» равна 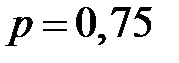 . Проведено
. Проведено 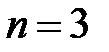 испытаний. Тогда по формуле Бернулли вероятность того, что «успех» появится ровно 2 раза (т.е. среди взятых наудачу трёх волокон окажутся 2 длинных волокна), равна
испытаний. Тогда по формуле Бернулли вероятность того, что «успех» появится ровно 2 раза (т.е. среди взятых наудачу трёх волокон окажутся 2 длинных волокна), равна
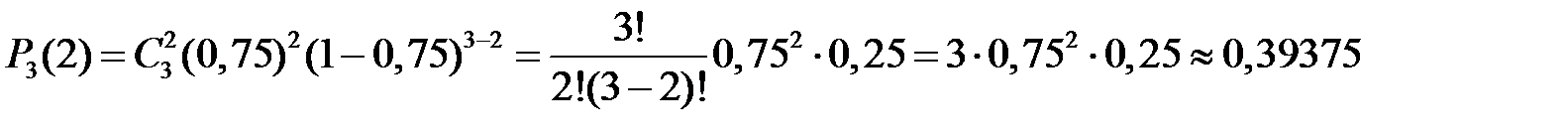 .
.
 2015-07-14
2015-07-14 1797
1797
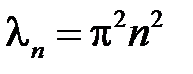 ,
, 






