1. Смешанная задача для однородного волнового уравнения на отрезке 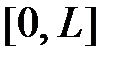 при нулевых граничных условиях
при нулевых граничных условиях 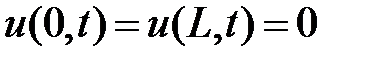 .
.
2. Плотность распределения вероятностей случайной величины. Её связь с функцией распределения. Вывести формулу для нахождения вероятности попадания случайной величины в промежуток 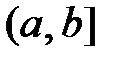 , если известна её плотность вероятности.
, если известна её плотность вероятности.
3. Найти решение смешанной задачи
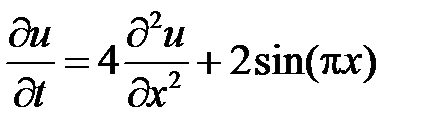 ,
, 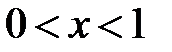 ,
,
ГУ: 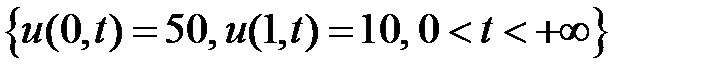 ; НУ:
; НУ: 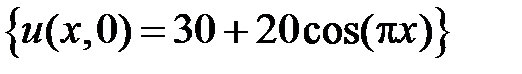 .
.
4. В первой коробке 20 радиоламп, из них 18 стандартных, а во второй 10, из которых 9 стандартных. Из второй коробки взята наудачу лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлечённая из первой коробки, будет стандартной.
1. Смешанная задача для однородного волнового уравнения на отрезке 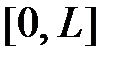 при нулевых граничных условиях имеет вид:
при нулевых граничных условиях имеет вид:
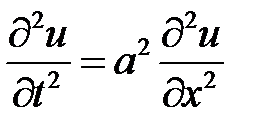 ,
, 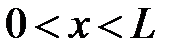 ,
, 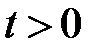 ,
,
граничные условия: 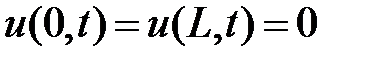 ;
;
начальные условия: 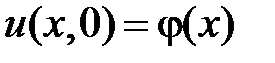 ,
, 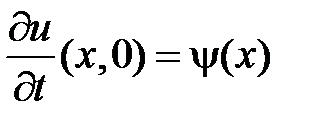 .
.
Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 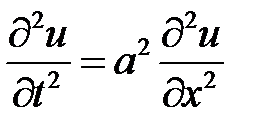 будем искать в виде
будем искать в виде 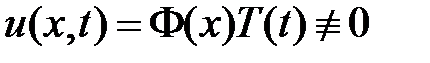 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
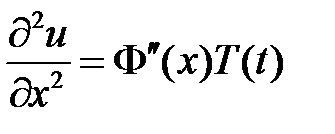 ,
, 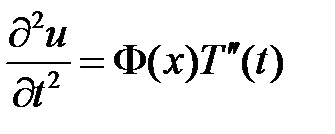 ,
,
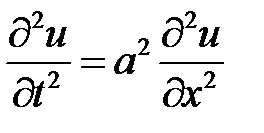 :
: 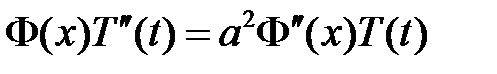 ,
,
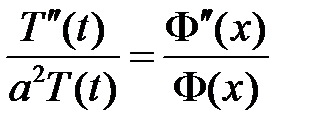 ,
, 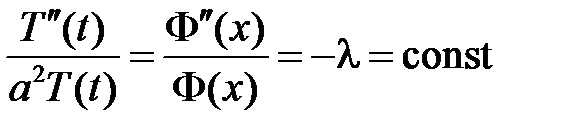 ,
, 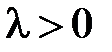 .
.
Тогда функции 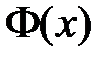 и
и 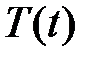 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 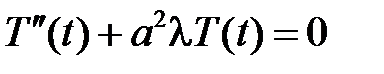 .
.
Из граничных условий 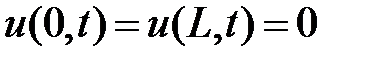 получаем краевые условия для функции
получаем краевые условия для функции 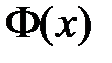 :
: 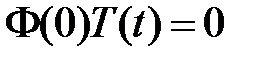 ,
, 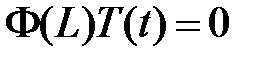 , значит,
, значит, 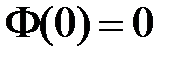 ,
, 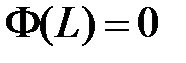 . Таким образом, для определения
. Таким образом, для определения 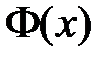 и
и 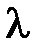 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

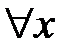 :
: 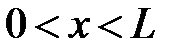 ,
,
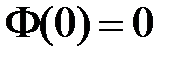 ,
, 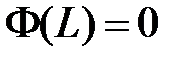 .
.
Поскольку 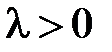 (при
(при 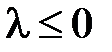 задача имеет только тривиальные решения), то общее решение уравнения
задача имеет только тривиальные решения), то общее решение уравнения  имеет вид
имеет вид
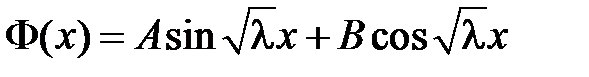 .
.
Из краевого условия 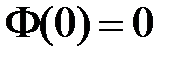 получаем:
получаем: 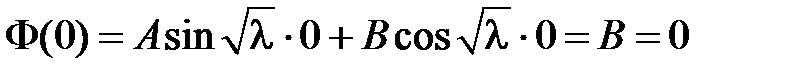 , т.е.
, т.е. 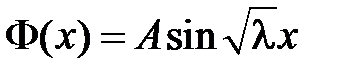 .
.
Из краевого условия 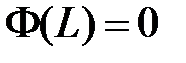 получаем:
получаем: 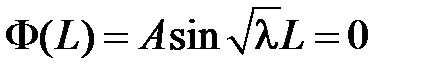 . Поскольку
. Поскольку 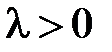 и
и 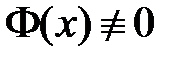 , то
, то 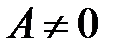 и равенство
и равенство 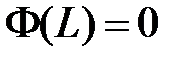 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 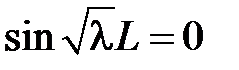 , откуда получаем
, откуда получаем 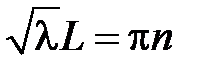 ,
,  , т.е.
, т.е. 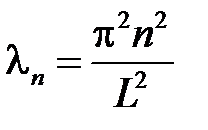 ,
,  . Тогда получим
. Тогда получим 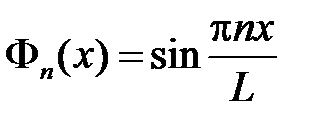 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 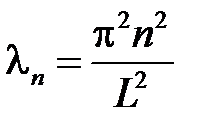 ,
,  ;
;
собственные функции 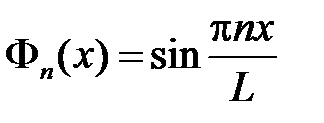 ,
,  .
.
Теперь при каждом 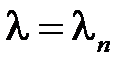 решаем уравнение для
решаем уравнение для 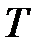 :
:
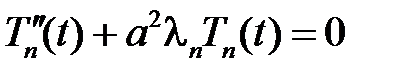 ,
,  .
.
Общее решение этого уравнения имеет вид
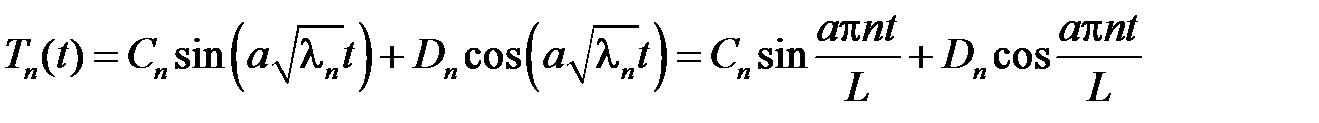 .
.
Тогда
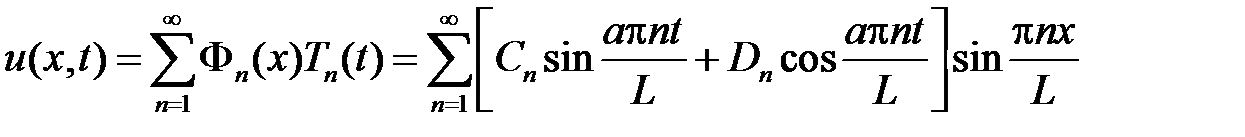 .
.
Для нахождения коэффициентов 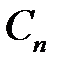 ,
, 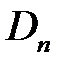 ,
,  , воспользуемся начальными условиями
, воспользуемся начальными условиями 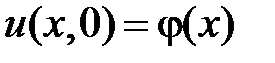 ,
, 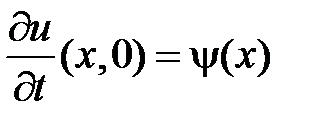 .
.
Разложим функции 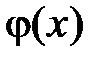 и
и 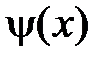 на отрезке
на отрезке 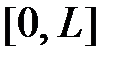 в ряды Фурье по системе
в ряды Фурье по системе 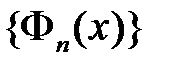 :
:
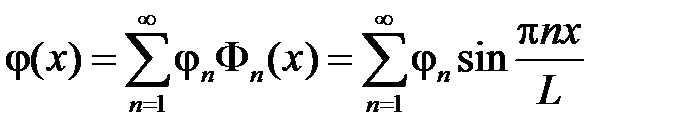 ,
,
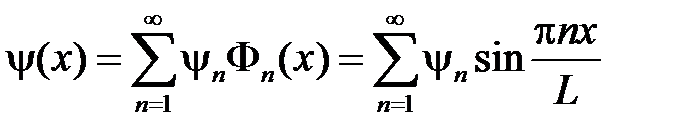 ,
,
где
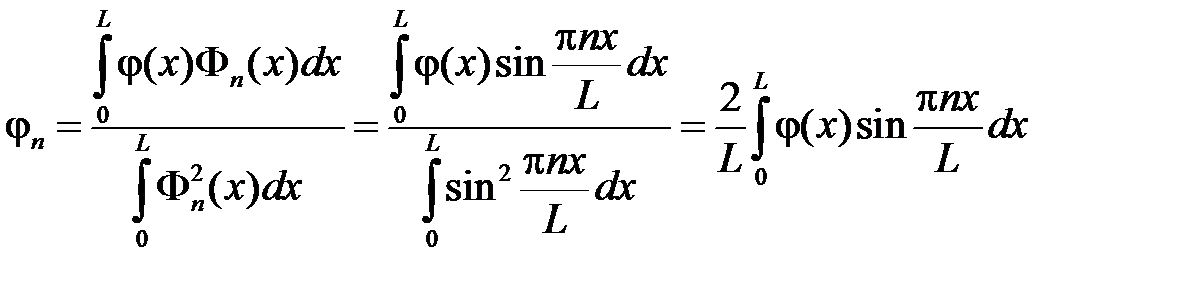 ,
,
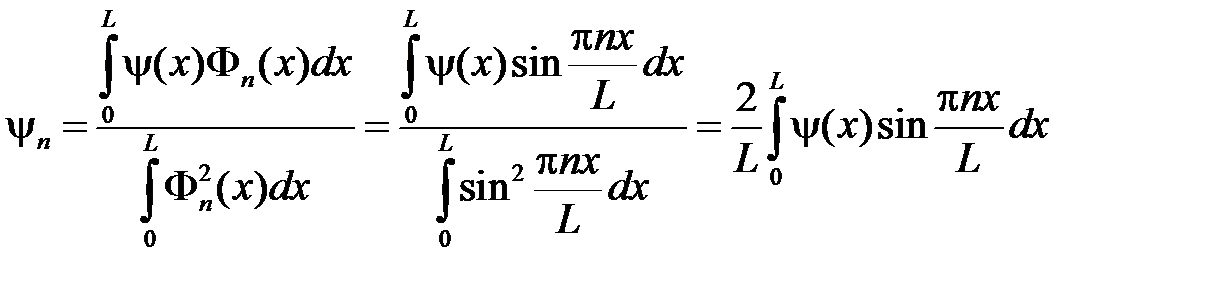 ,
,
так как 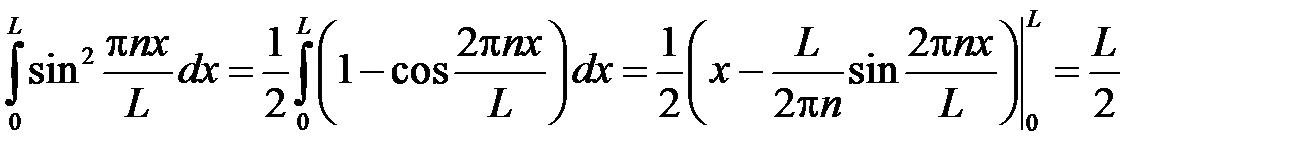 .
.
Тогда начальное условие 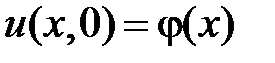 дает
дает
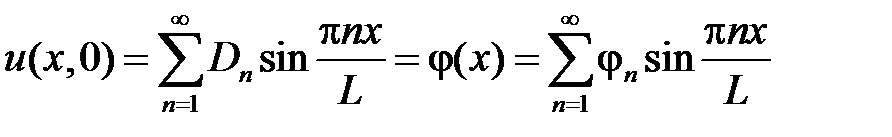 ,
,
откуда
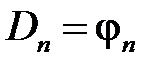 ,
, 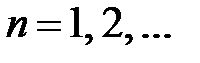 .
.
Находим 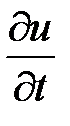 :
:
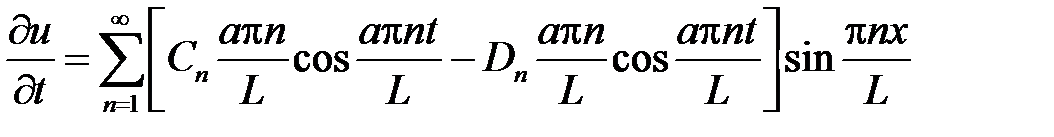 .
.
Тогда начальное условие 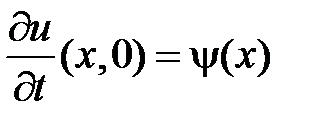 дает
дает
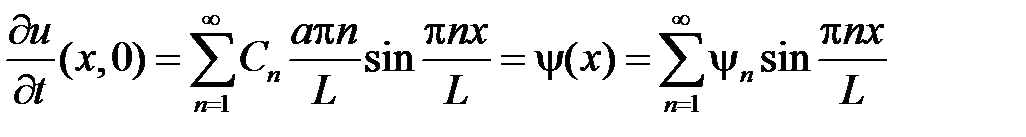 ,
,
откуда
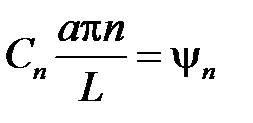 ,
, 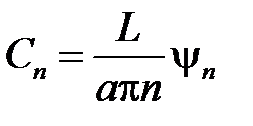 ,
,  .
.
Тогда решением задачи является ряд
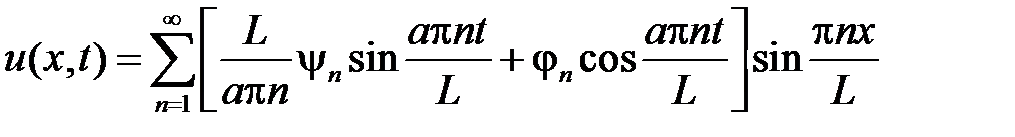 .
.
2. Пусть 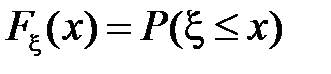 – функция распределения случайной величины
– функция распределения случайной величины 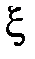 . Функцию
. Функцию 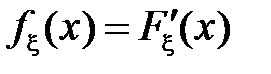 называют плотностью распределения вероятностей случайной величины
называют плотностью распределения вероятностей случайной величины 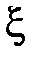 (или плотностью вероятности).
(или плотностью вероятности).
Из равенства 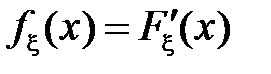 следует, что
следует, что 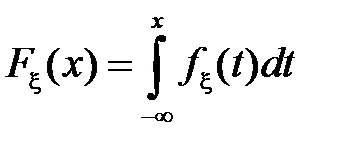 . Действительно, так как
. Действительно, так как 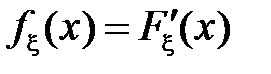 , то
, то 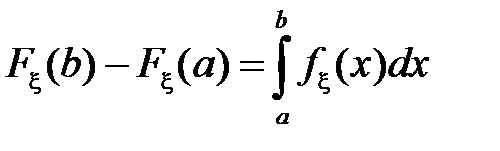 . Тогда, т.к.
. Тогда, т.к. 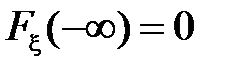 ,
,
 .
.
Кроме того, поскольку 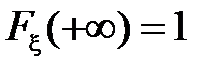 , то
, то 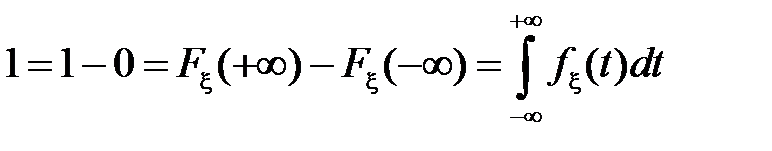 .
.
Условие 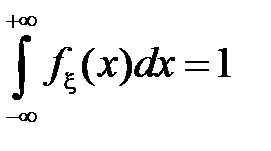 называется условием нормировки.
называется условием нормировки.
С помощью плотности распределения вероятностей можно рассчитывать вероятность попадания случайной величины 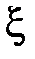 в промежуток
в промежуток 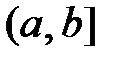 . Поскольку
. Поскольку
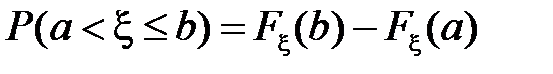 ,
,
то
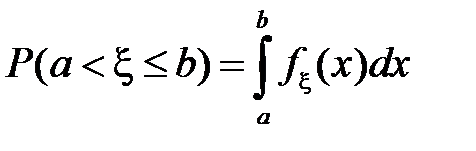 .
.
3. Поскольку граничные условия задачи 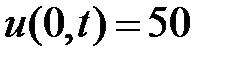 ,
, 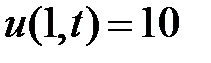 – неоднородные, то сначала сделаем замену, сводящую к однородным краевым условиям. Положим
– неоднородные, то сначала сделаем замену, сводящую к однородным краевым условиям. Положим
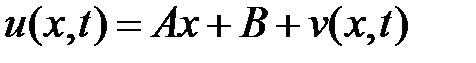 ,
,
где 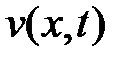 – новая неизвестная функция, а числа
– новая неизвестная функция, а числа 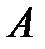 и
и 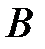 подберем так, чтобы
подберем так, чтобы 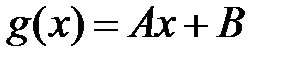 удовлетворяла граничным условиям:
удовлетворяла граничным условиям: 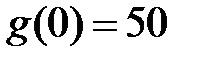 ,
, 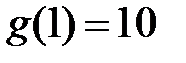 . Тогда
. Тогда
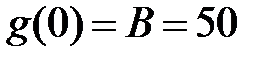 ,
, 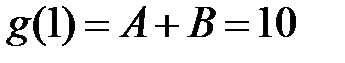 ,
,
откуда 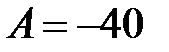 ,
, 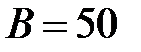 .
.
Итак, делаем замену
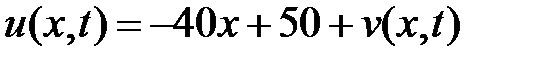 .
.
Тогда
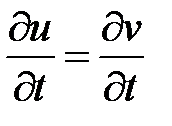 ,
, 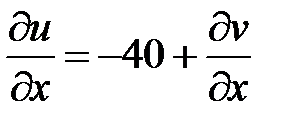 ,
, 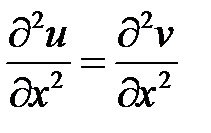 ,
,
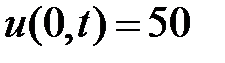 :
: 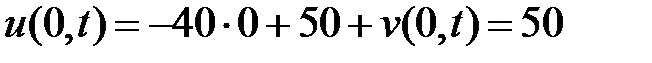
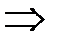
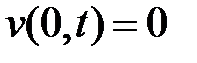 ,
,
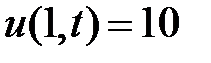 :
: 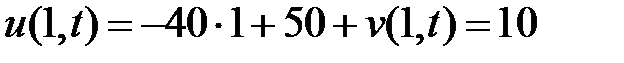
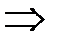
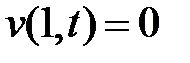 ,
,
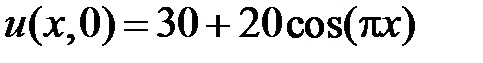 :
: 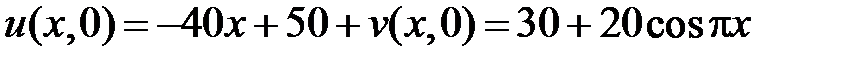
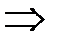
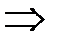
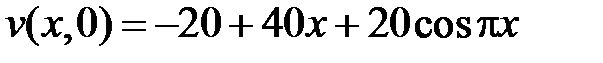 .
.
Итак, для функции 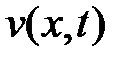 получим смешанную задачу
получим смешанную задачу
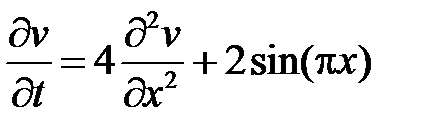 ,
, 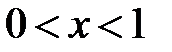 ,
, 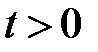 ,
,
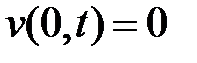 ,
, 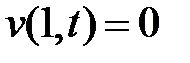 ,
,
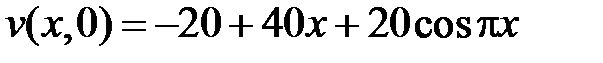 .
.
Уравнение задачи является неоднородным. Для решения задачи воспользуемся методом Фурье (разделения переменных). Рассмотрим соответствующее однородное уравнение 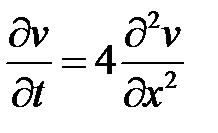 . Его нетривиальные решения будем искать в виде
. Его нетривиальные решения будем искать в виде 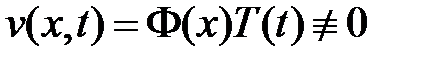 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
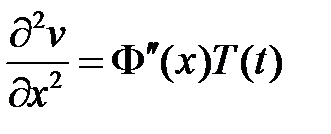 ,
, 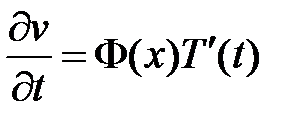 ,
,
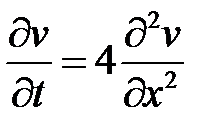 :
: 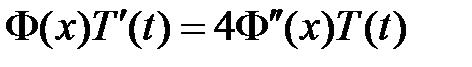 ,
,
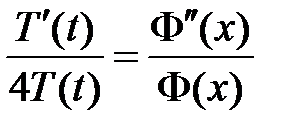 ,
, 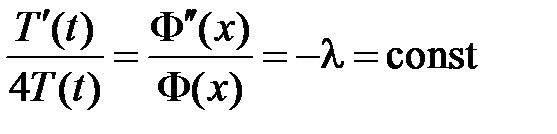 ,
, 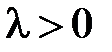 .
.
Тогда функция 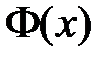 является решением уравнения
является решением уравнения
 .
.
Из граничных условий 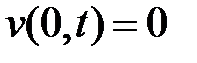 ,
, 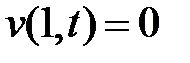 получаем краевые условия для функции
получаем краевые условия для функции 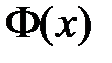 :
: 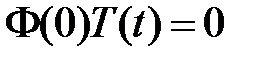 ,
, 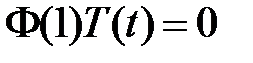 , значит,
, значит, 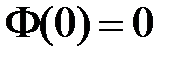 ,
, 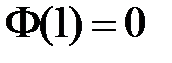 . Таким образом, для определения
. Таким образом, для определения 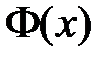 и
и 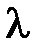 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

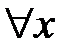 :
: 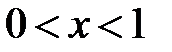 ,
,
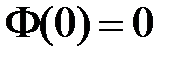 ,
, 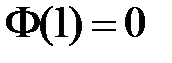 .
.
Поскольку 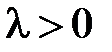 (при
(при 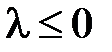 задача имеет только тривиальные решения), то общее решение уравнения
задача имеет только тривиальные решения), то общее решение уравнения  имеет вид
имеет вид
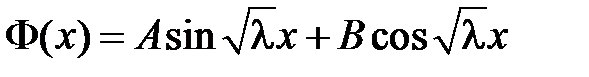 .
.
Из краевого условия 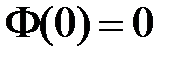 получаем:
получаем: 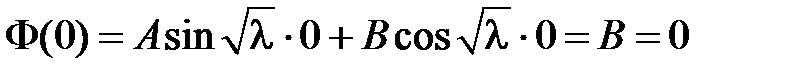 , т.е.
, т.е. 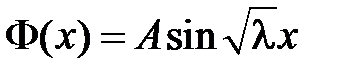 .
.
Из краевого условия 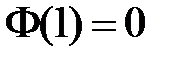 получаем:
получаем: 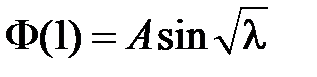 . Поскольку
. Поскольку 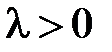 и
и 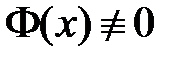 , то
, то 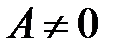 и равенство
и равенство 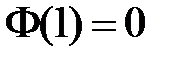 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 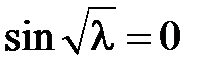 , откуда получаем
, откуда получаем 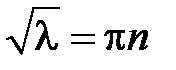 ,
,  , т.е.
, т.е. 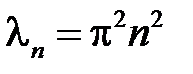 ,
,  . Тогда получим
. Тогда получим 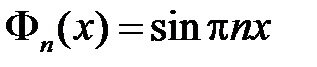 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 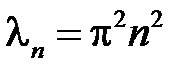 ,
,  ;
;
собственные функции 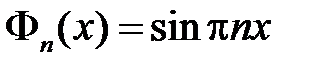 ,
,  .
.
Тогда решение смешанной задачи для неоднородного уравнения будем искать в виде
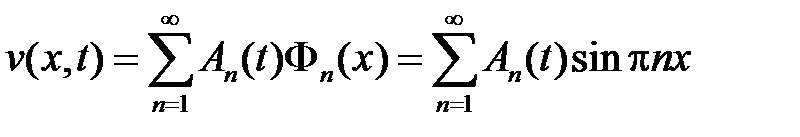 ,
,
где функции 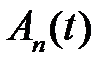 ,
,  , подберем так, чтобы удовлетворить неоднородному уравнению и начальному условию. Заметим, что функция
, подберем так, чтобы удовлетворить неоднородному уравнению и начальному условию. Заметим, что функция 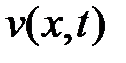 при любом выборе функций
при любом выборе функций 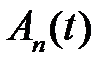 ,
,  , точно удовлетворяет однородным граничным условиям
, точно удовлетворяет однородным граничным условиям 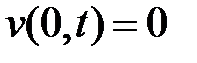 ,
, 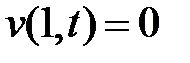 . Находим производные
. Находим производные
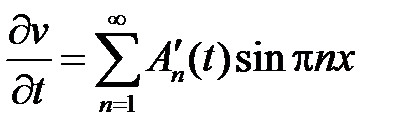 ,
, 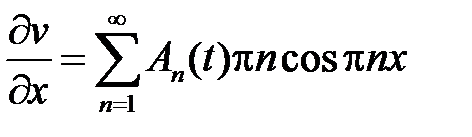 ,
, 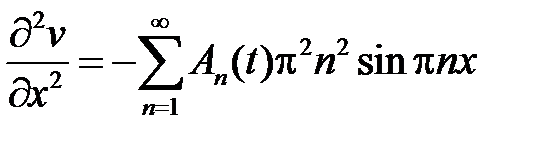
и подставляем их в неоднородное уравнение 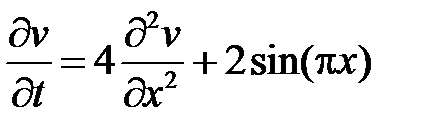 :
:
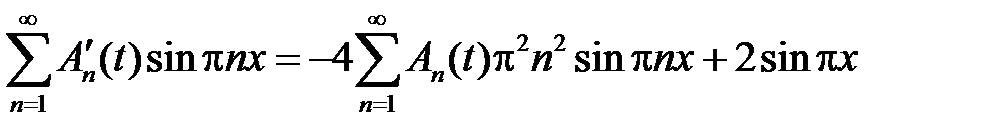 ,
,
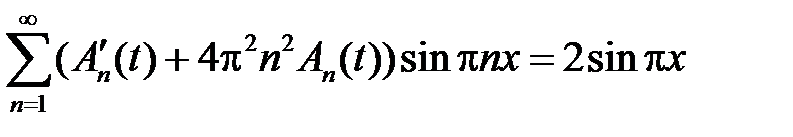 .
.
Тогда функции 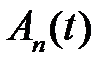 ,
,  , удовлетворяют уравнениям
, удовлетворяют уравнениям
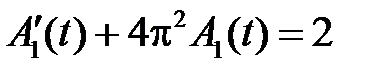 ,
,
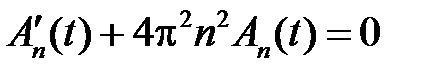 ,
, 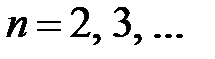 .
.
Начальные условия для этих уравнений получим, подставив 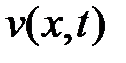 в начальное условие
в начальное условие 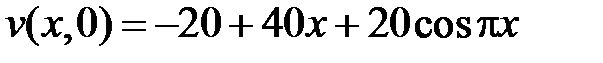 , которое сначала представим на отрезке
, которое сначала представим на отрезке 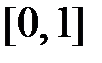 в виде ряда Фурье по системе функций
в виде ряда Фурье по системе функций 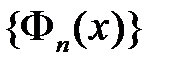 :
:
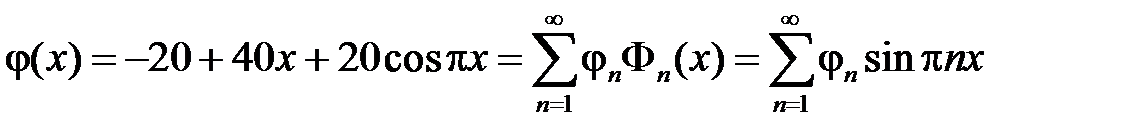 ,
,
где
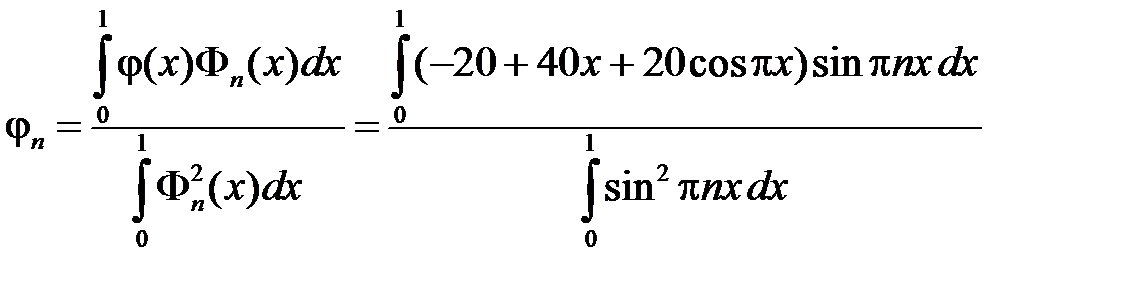 .
.
Находим
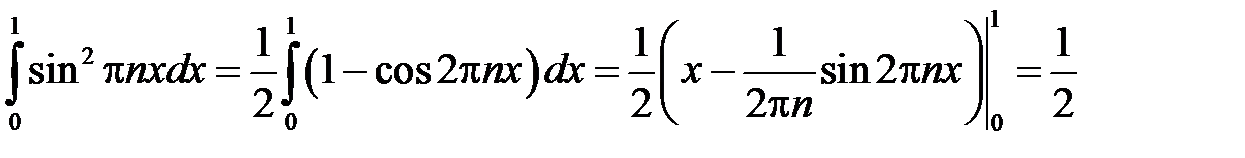 ,
,
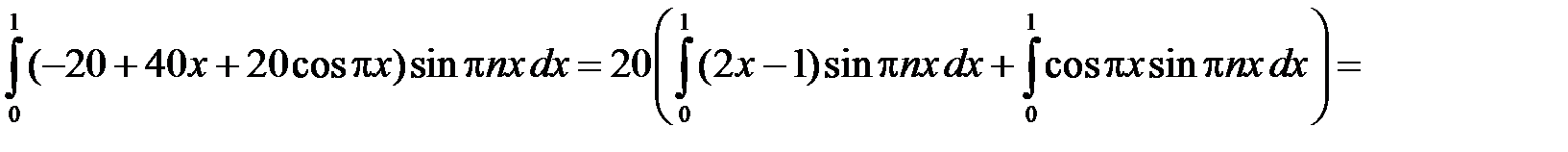
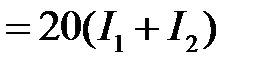 ,
,
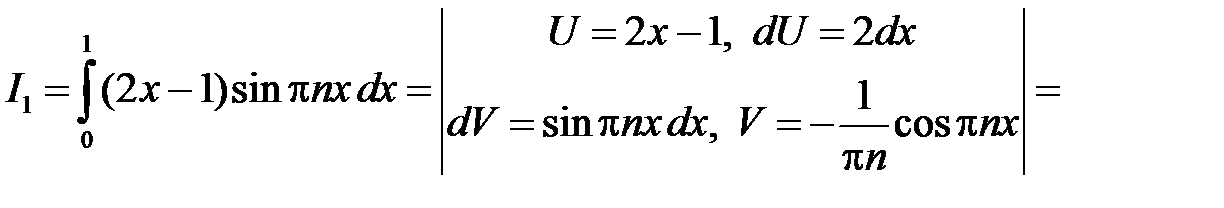
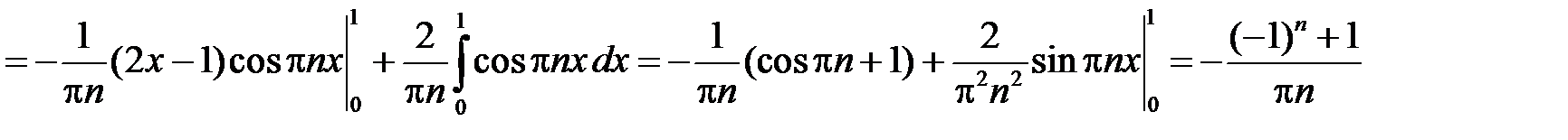 ,
,
при 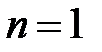
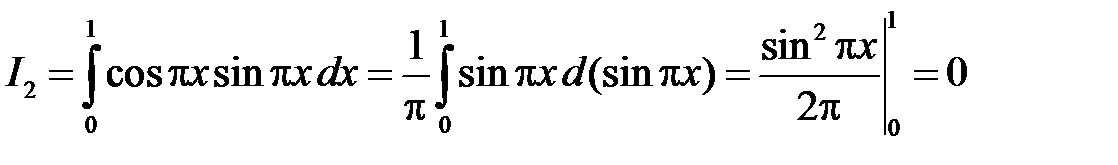 ,
,
при 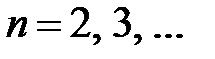
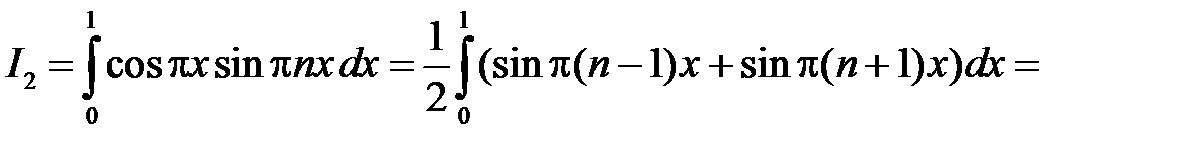
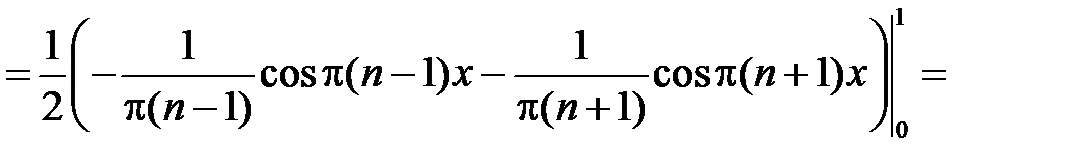
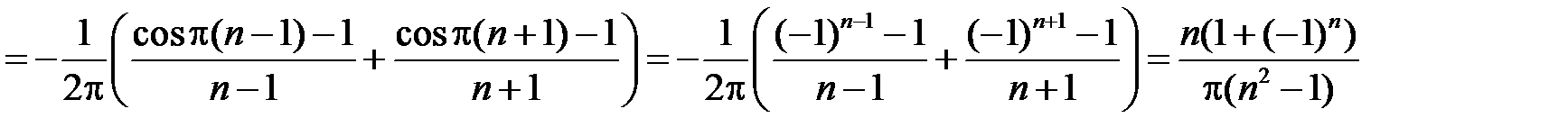 .
.
Таким образом,
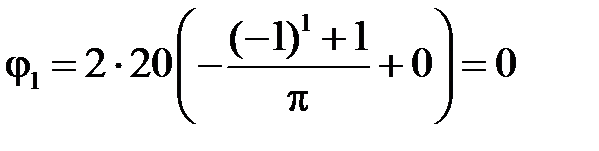
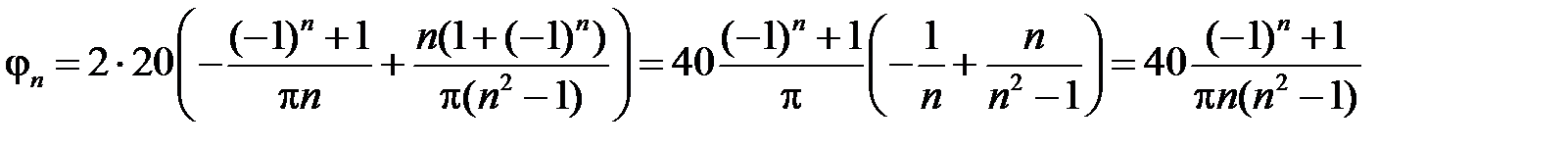 ,
,
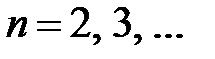 .
.
Если 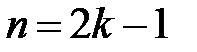 ,
, 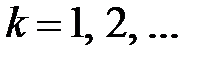 , то
, то  , если
, если 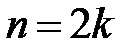 ,
, 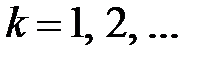 , то
, то 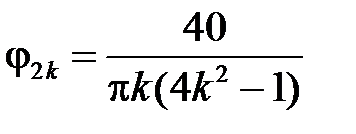 .
.
Итак,
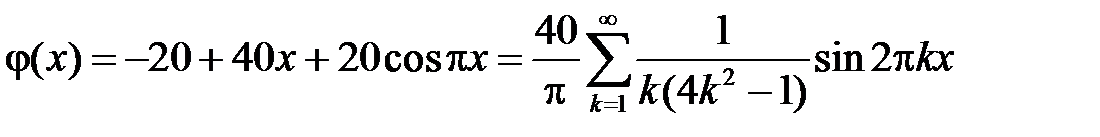 .
.
Тогда начальное условие 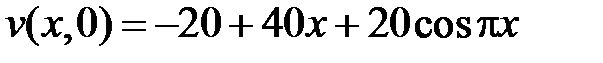 дает
дает
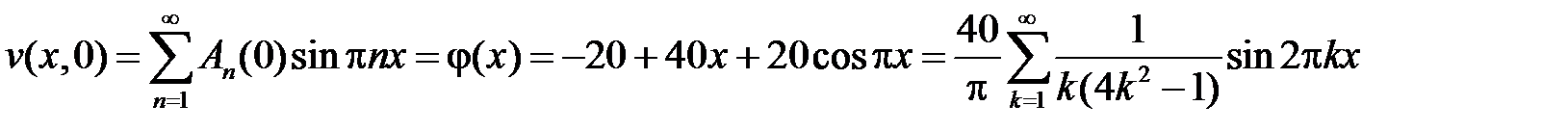 ,
,
откуда получим начальные условия для 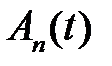 :
:
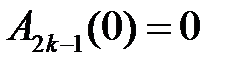 ,
, 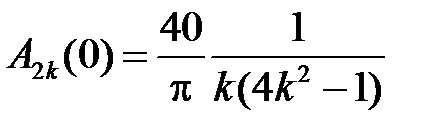 ,
, 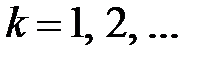
Тогда для 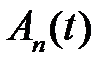 ,
,  , получим задачи Коши
, получим задачи Коши
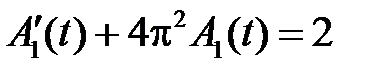 ,
, 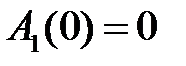 ,
,
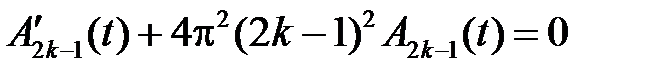 ,
, 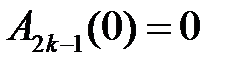 ,
, 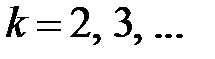 ,
,
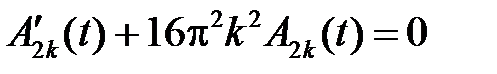 ,
, 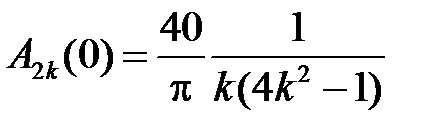 ,
, 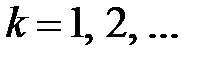 .
.
Решаем эти задачи:
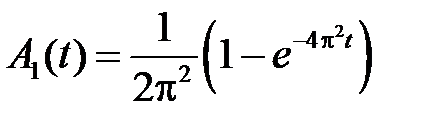 ,
, 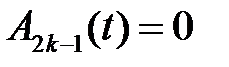 ,
, 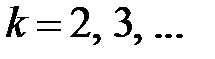 ,
,
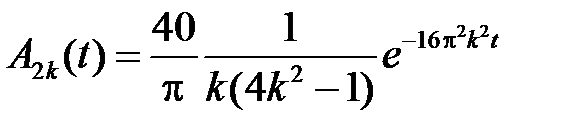 ,
, 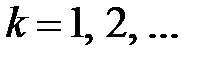 .
.
Тогда
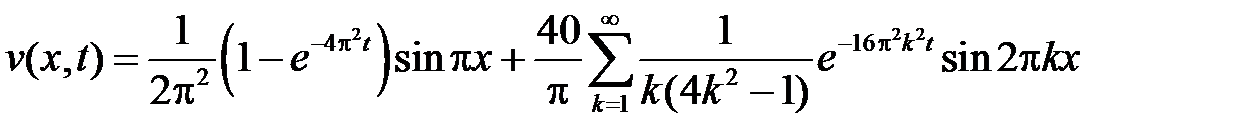 .
.
Возвращаясь к неизвестной функции 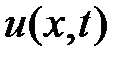 по формуле
по формуле 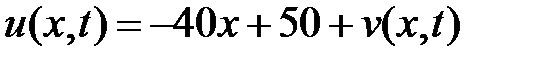 , получим
, получим
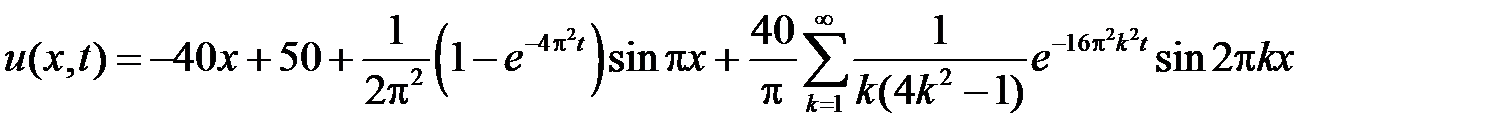 .
.
4. Воспользуемся формулой полной вероятности. Событие
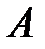 – лампа, наудачу извлечённая из первой коробки, будет стандартной.
– лампа, наудачу извлечённая из первой коробки, будет стандартной.
Введем гипотезы:
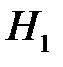 – из второй коробки в первую переложена стандартная лампа;
– из второй коробки в первую переложена стандартная лампа;
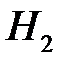 – из второй коробки в первую переложена нестандартная лампа.
– из второй коробки в первую переложена нестандартная лампа.
Поскольку всего во второй коробке 10 ламп, из которых 9 стандартных, то вероятности гипотез
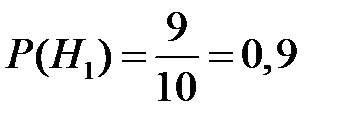 ,
, 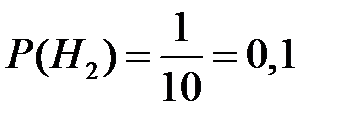 .
.
Найдем условные вероятности 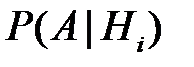 ,
, 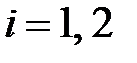 .
.
Если из второй коробки в первую переложили стандартную лампу (гипотеза 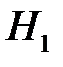 ), то в первой коробке стало 21 радиолампа, из которых 19 стандартных, значит,
), то в первой коробке стало 21 радиолампа, из которых 19 стандартных, значит,
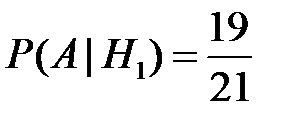 .
.
Если из второй коробки в первую переложили нестандартную лампу (гипотеза 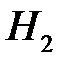 ), то в первой коробке стало 21 радиолампа, из которых 18 стандартных, значит,
), то в первой коробке стало 21 радиолампа, из которых 18 стандартных, значит,
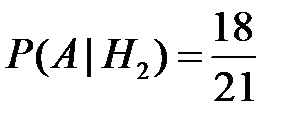 .
.
Тогда по формуле полной вероятности
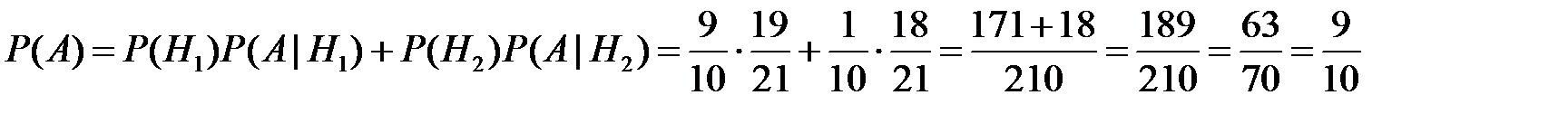 .
.
 2015-07-14
2015-07-14 440
440








