1. Смешанная задача для однородного волнового уравнения на полупрямой.
2. Теорема умножения вероятностей (с доказательством).
3. Найти решение смешанной задачи
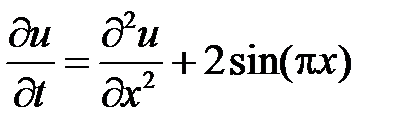 ,
, 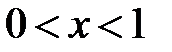 ,
,
ГУ: 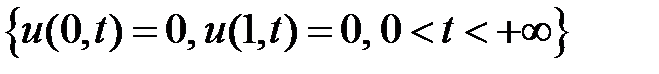 ; НУ:
; НУ: 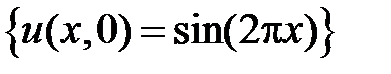 .
.
4. Случайная величина 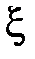 принимает только 2 значения: 1 и (–1), каждое с вероятностью 0,5. Найти дисперсию и среднее квадратическое отклонение этой случайной величины.
принимает только 2 значения: 1 и (–1), каждое с вероятностью 0,5. Найти дисперсию и среднее квадратическое отклонение этой случайной величины.
1. Задача Коши для одномерного волнового уравнения на полупрямой имеет вид:
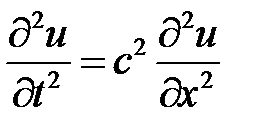 ,
, 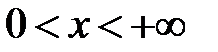 ,
, 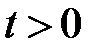 ,
,
начальные условия: 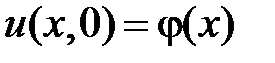 ,
, 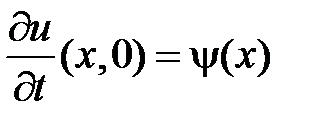
краевое условие: 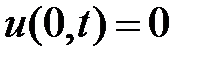 .
.
Рассмотрим сначала задачу на всей прямой и предположим, что функции 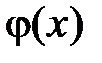 и
и 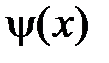 в начальных условиях нечетные, т.е.
в начальных условиях нечетные, т.е. 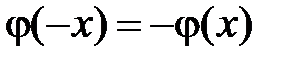 и
и 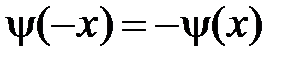 . Решение задачи Коши для одномерного волнового уравнения на всей прямой дается формулой Даламбера
. Решение задачи Коши для одномерного волнового уравнения на всей прямой дается формулой Даламбера
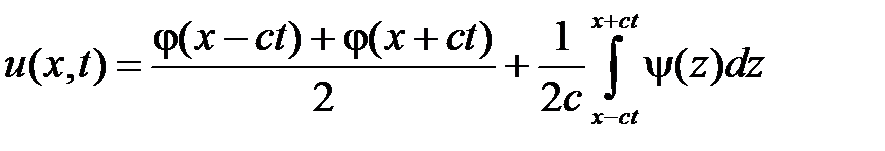 .
.
Найдем 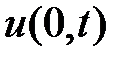 :
:
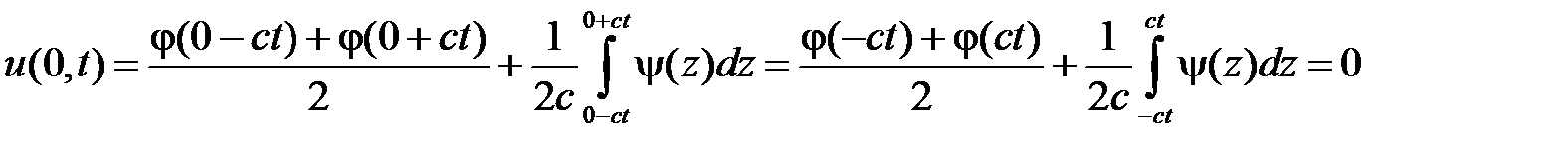
(интеграл равен нулю как интеграл от нечетной функции по симметричному относительно нуля промежутку интегрирования).
Итак, если в задаче Коши на прямой начальные данные – нечетные функции, то в любой момент времени будет выполнено 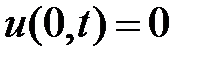 .
.
Тогда решение задачи Коши для одномерного волнового уравнения на полупрямой записывается по формуле Даламбера
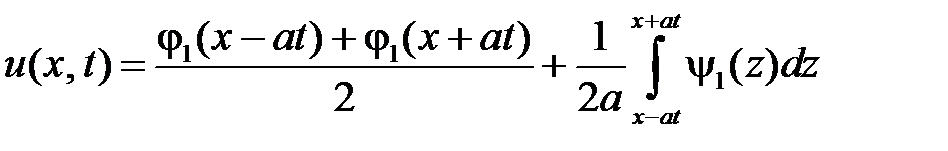 ,
,
где 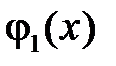 ,
, 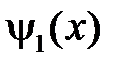 продолженные нечётным образом на отрицательную часть оси
продолженные нечётным образом на отрицательную часть оси 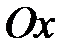 функции
функции 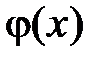 и
и 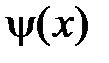 соответственно, то есть
соответственно, то есть
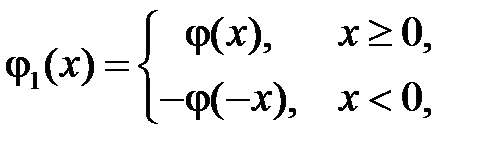
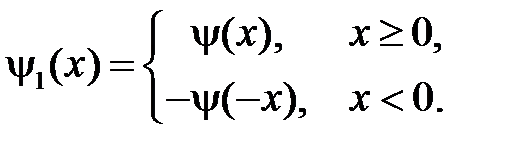
2. Обозначим условную вероятность 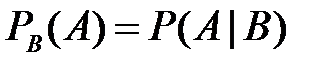 – вероятность события
– вероятность события 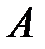 при условии, что событие
при условии, что событие 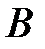 произошло.
произошло.
Теорема. Для любых событий 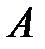 и
и 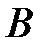 ,
, 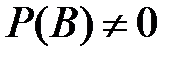 ,
,
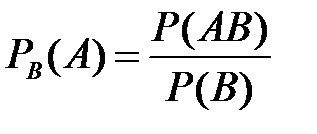 .
.
Доказательство. Пусть 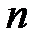 – числе всех равновозможных исходов испытания, в результате которого могут появиться события
– числе всех равновозможных исходов испытания, в результате которого могут появиться события 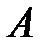 и
и 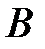 . Пусть
. Пусть 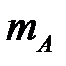 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 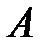 ,
, 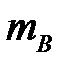 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 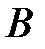 ,
, 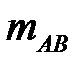 – число тех исходов, которые благоприятствуют произведению событий
– число тех исходов, которые благоприятствуют произведению событий 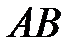 . Тогда по формуле классической вероятности
. Тогда по формуле классической вероятности
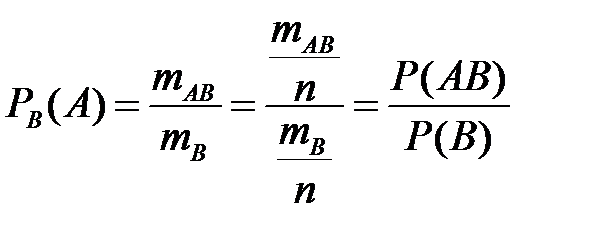 .
.
Аналогично получаем
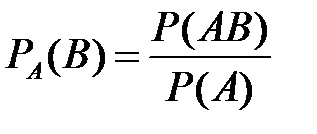 .
.
Из этих формул следует теорема умножения вероятностей:
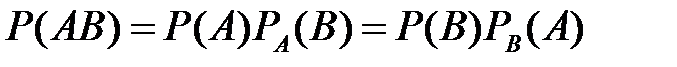 .
.
События  и
и 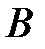 называются независимыми, если вероятность появления одного из них не меняется в зависимости от того, появилось другое событие или нет.
называются независимыми, если вероятность появления одного из них не меняется в зависимости от того, появилось другое событие или нет.
В этом случае:
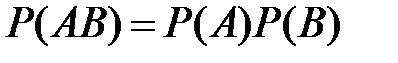 .
.
Для трех событий 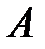 ,
, 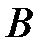 и
и  теорема умножения имеет вид
теорема умножения имеет вид
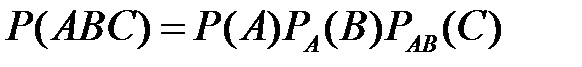 ,
,
а для независимых событий
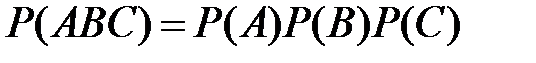 .
.
3. Уравнение задачи является неоднородным. Для решения задачи воспользуемся методом Фурье (разделения переменных). Рассмотрим соответствующее однородное уравнение 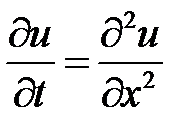 . Его нетривиальные решения будем искать в виде
. Его нетривиальные решения будем искать в виде 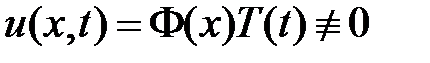 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
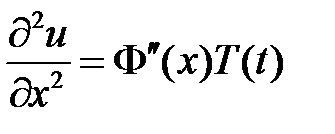 ,
, 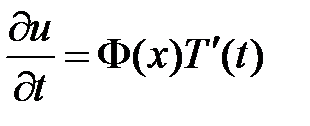 ,
,
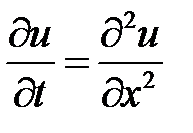 :
: 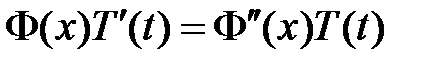 ,
,
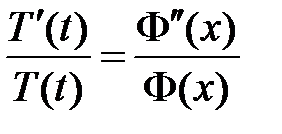 ,
, 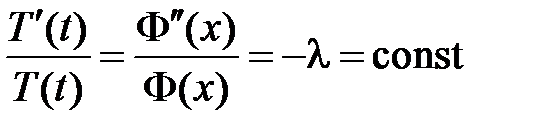 ,
, 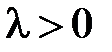 .
.
Тогда функции 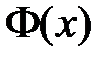 и
и 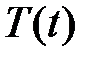 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 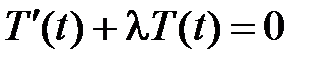 .
.
Из граничных условий 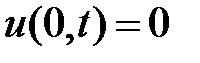 ,
, 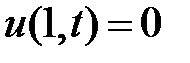 получаем краевые условия для функции
получаем краевые условия для функции 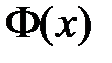 :
: 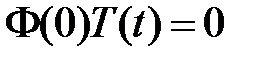 ,
, 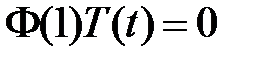 , значит,
, значит, 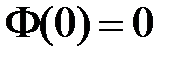 ,
, 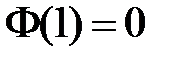 . Таким образом, для определения
. Таким образом, для определения 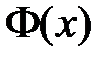 и
и 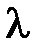 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

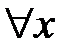 :
: 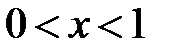 ,
,
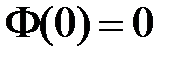 ,
, 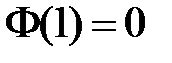 .
.
Поскольку 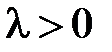 (при
(при 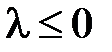 задача имеет только тривиальные решения), то общее решение уравнения
задача имеет только тривиальные решения), то общее решение уравнения  имеет вид
имеет вид
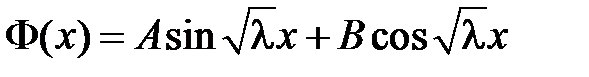 .
.
Из краевого условия 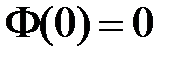 получаем:
получаем: 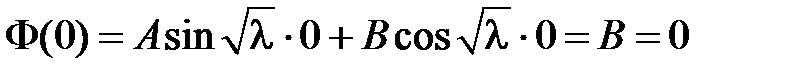 , т.е.
, т.е. 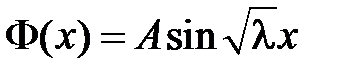 .
.
Из краевого условия 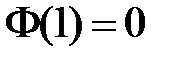 получаем:
получаем: 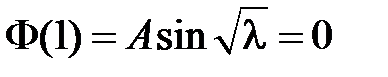 . Поскольку
. Поскольку 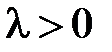 и
и 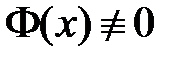 , то
, то 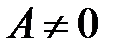 и равенство
и равенство 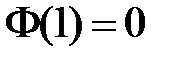 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 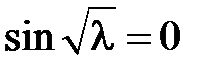 , откуда получаем
, откуда получаем 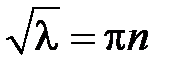 ,
,  , т.е.
, т.е. 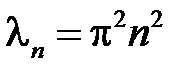 ,
,  . Тогда получим
. Тогда получим 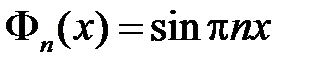 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 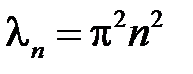 ,
,  ;
;
собственные функции 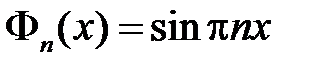 ,
,  .
.
Тогда решение смешанной задачи для неоднородного уравнения будем искать в виде
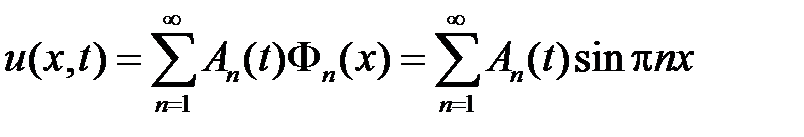 ,
,
где функции 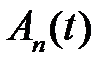 ,
,  , подберем так, чтобы удовлетворить неоднородному уравнению и начальному условию. Заметим, что функция
, подберем так, чтобы удовлетворить неоднородному уравнению и начальному условию. Заметим, что функция 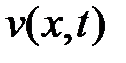 при любом выборе функций
при любом выборе функций 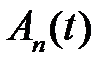 ,
,  , точно удовлетворяет однородным граничным условиям
, точно удовлетворяет однородным граничным условиям 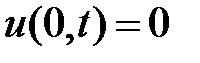 ,
, 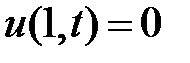 . Находим производные
. Находим производные
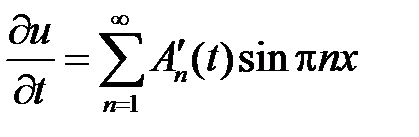 ,
, 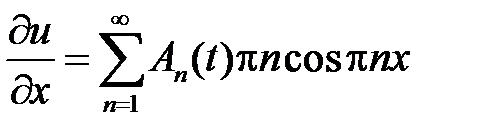 ,
, 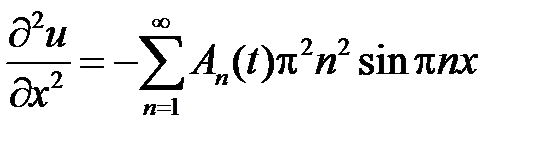
и подставляем их в неоднородное уравнение 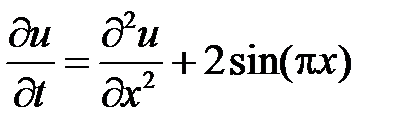 :
:
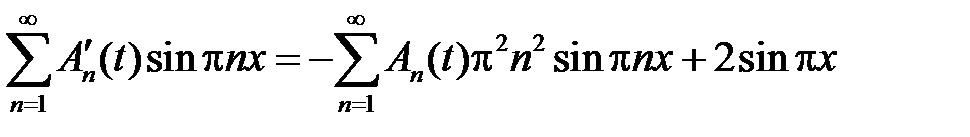 ,
,
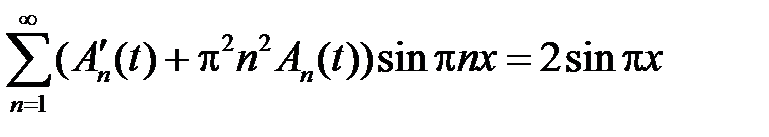 .
.
Тогда функции 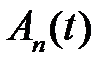 ,
,  , удовлетворяют уравнениям
, удовлетворяют уравнениям
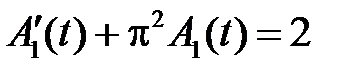 ,
,
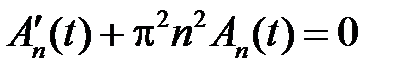 ,
, 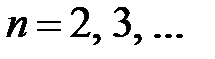 .
.
Начальные условия для этих уравнений получим, подставив 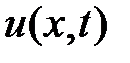 в начальное условие
в начальное условие 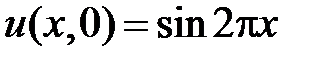 :
:
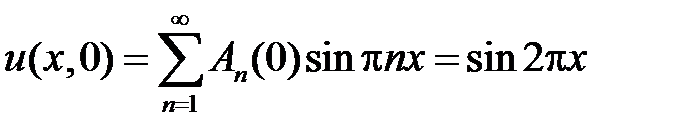 ,
,
откуда получим начальные условия для 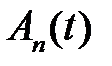 :
:
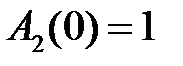 ,
, 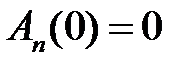 ,
, 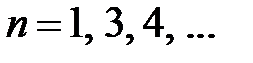
Тогда для 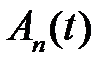 ,
,  , получим задачи Коши
, получим задачи Коши
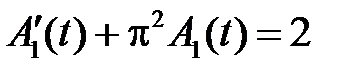 ,
, 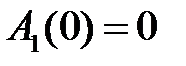 ,
,
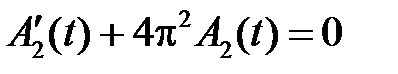 ,
, 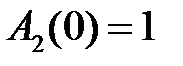 ,
,
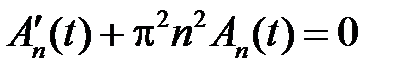 ,
, 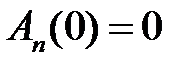 ,
, 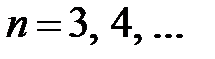 .
.
Решаем эти задачи:
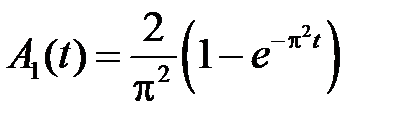 ,
, 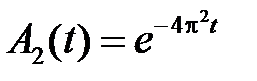 ,
,
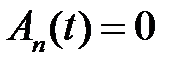 ,
, 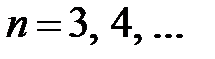 .
.
Тогда
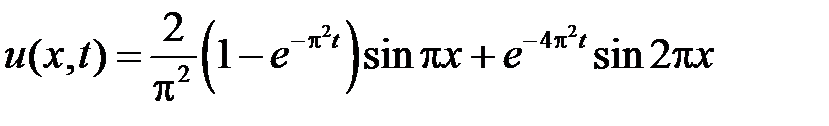 .
.
4. Ряд распределения по условию имеет вид
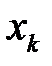
| –1 | |
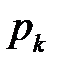
| 0,5 | 0,5 |
Математическое ожидание и дисперсия дискретной случайной величины находятся соответственно по формулам
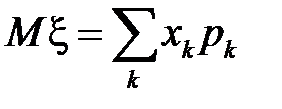 ,
, 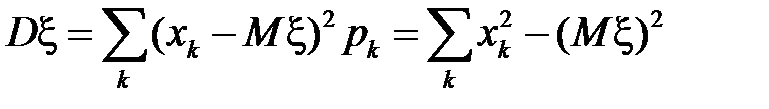 .
.
Тогда
математическое ожидание:
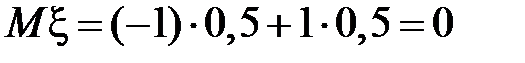 ,
,
дисперсия:
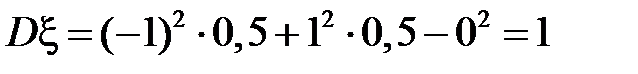 ,
,
среднее квадратическое отклонение:
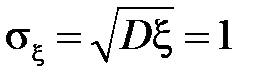 .
.
 2015-07-14
2015-07-14 416
416








