1. Смешанная задача для однородного уравнения теплопроводности на отрезке 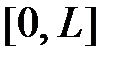 при нулевых граничных условиях
при нулевых граничных условиях 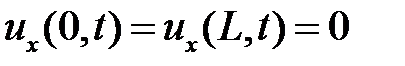 .
.
2. Вывести формулу для нахождения вероятности попадания случайной величины 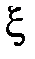 в промежуток
в промежуток 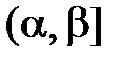 , если
, если 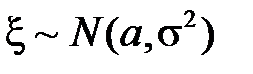 .
.
3. Найти решение задачи Коши для волнового уравнения
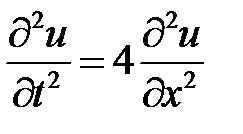 ,
,
НУ: 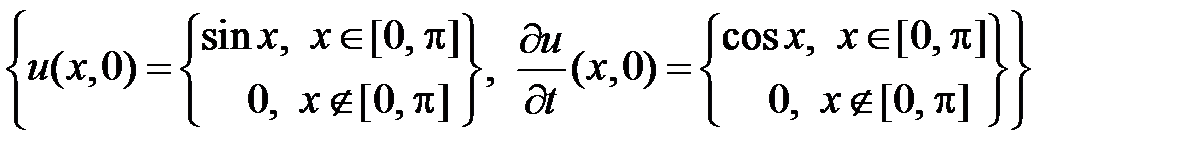 .
.
4. Имеется два ящика, содержащих по десять деталей. В первом из них 8, а во втором 7 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе вынутые детали окажутся стандартными.
1. Смешанная задача для однородного уравнения теплопроводности на отрезке 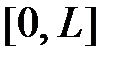 при нулевых граничных условиях имеет вид:
при нулевых граничных условиях имеет вид:
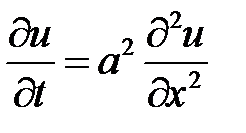 ,
, 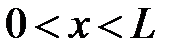 ,
, 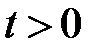 ,
,
граничные условия: 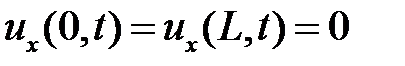 ;
;
начальное условие: 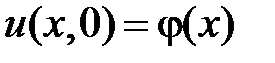 .
.
Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 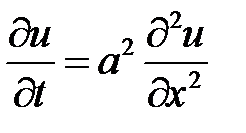 будем искать в виде
будем искать в виде 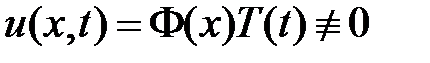 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
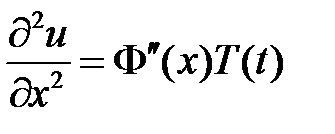 ,
, 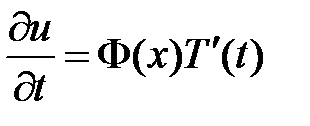 ,
,
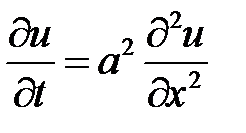 :
: 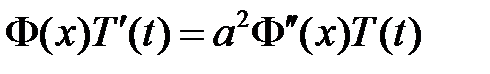 ,
,
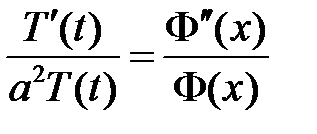 ,
, 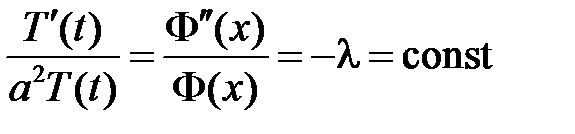 ,
, 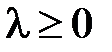 .
.
Тогда функции 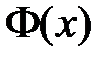 и
и 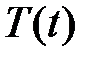 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 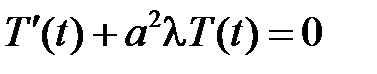 .
.
Из граничных условий 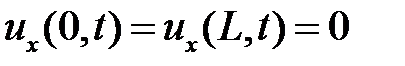 получаем краевые условия для функции
получаем краевые условия для функции 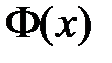 :
: 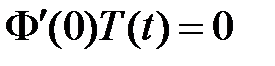 ,
, 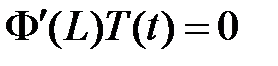 , значит,
, значит, 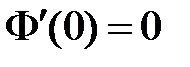 ,
, 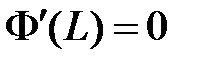 . Таким образом, для определения
. Таким образом, для определения 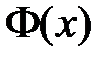 и
и 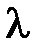 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

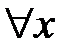 :
: 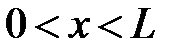 ,
,
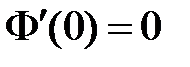 ,
, 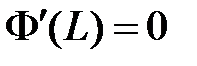 .
.
Поскольку мы имеем дело со второй краевой задачей, то 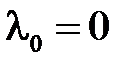 является собственным значением, а
является собственным значением, а 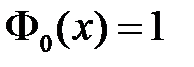 – соответствующей ему собственной функцией.
– соответствующей ему собственной функцией.
Пусть теперь 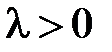 (при
(при 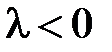 задача имеет только тривиальные решения). Общее решение уравнения
задача имеет только тривиальные решения). Общее решение уравнения  имеет вид
имеет вид
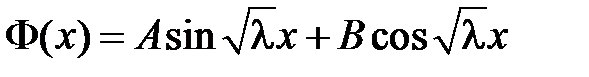 .
.
Тогда 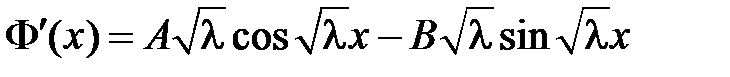 . Из краевого условия
. Из краевого условия 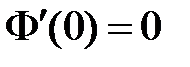 получаем:
получаем: 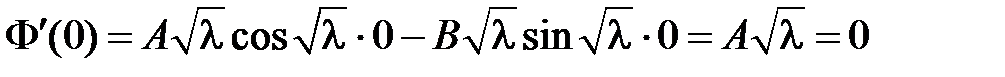 ,
, 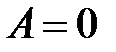 , т.е.
, т.е. 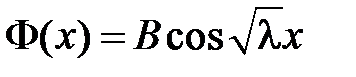 и
и 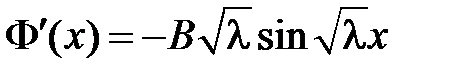 .
.
Из краевого условия 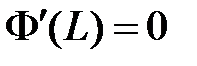 получаем:
получаем: 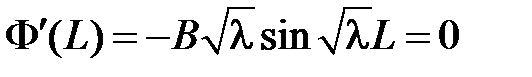 . Поскольку
. Поскольку 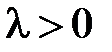 и
и 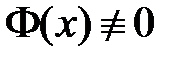 , то
, то 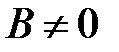 и равенство
и равенство 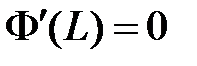 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 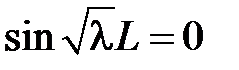 , откуда получаем
, откуда получаем 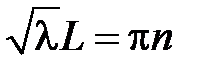 ,
,  , т.е.
, т.е. 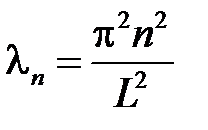 ,
,  . Тогда получим
. Тогда получим 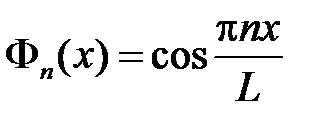 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 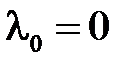 ,
, 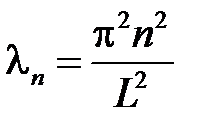 ,
,  ;
;
собственные функции 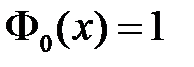 ,
, 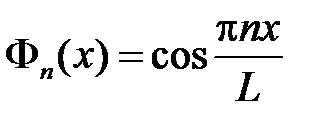 ,
,  .
.
Теперь при каждом 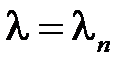 решаем уравнение для
решаем уравнение для 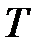 :
:
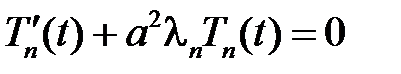 ,
, 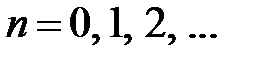 .
.
При 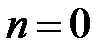 получим уравнение
получим уравнение 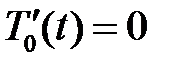 , откуда
, откуда
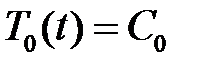 .
.
При  общее решение этого уравнения имеет вид
общее решение этого уравнения имеет вид
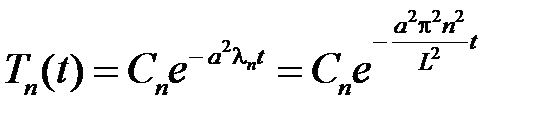 .
.
Тогда
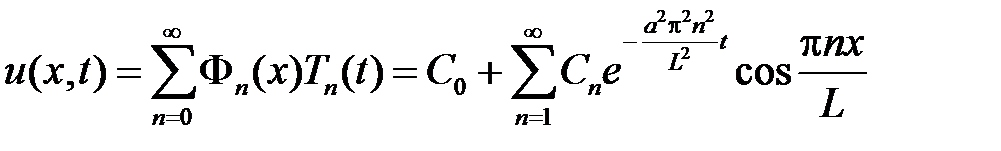 .
.
Для нахождения коэффициентов 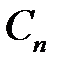 ,
, 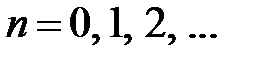 , воспользуемся начальным условием
, воспользуемся начальным условием 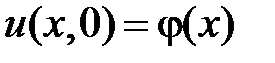 .
.
Разложим функцию 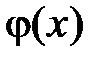 на отрезке
на отрезке 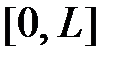 в ряд Фурье по системе
в ряд Фурье по системе 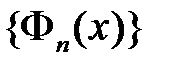 :
:
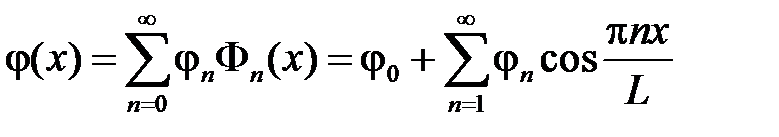 ,
,
где
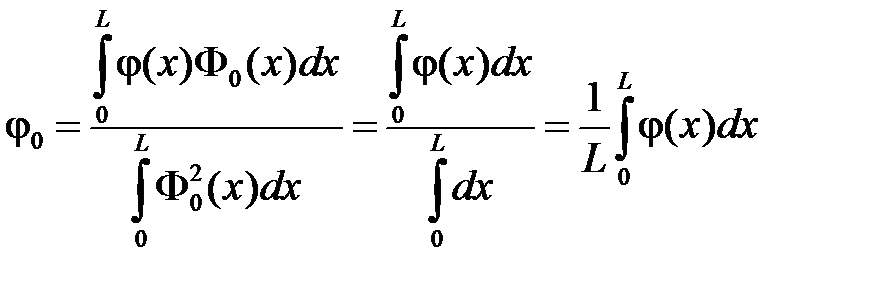 ,
,
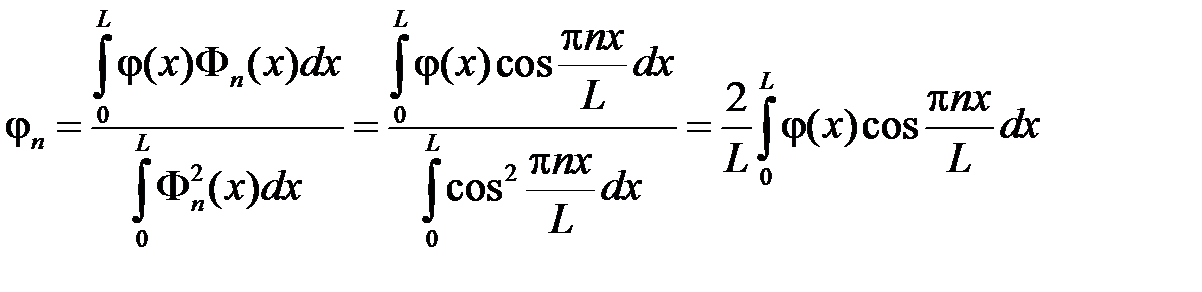 ,
,
так как 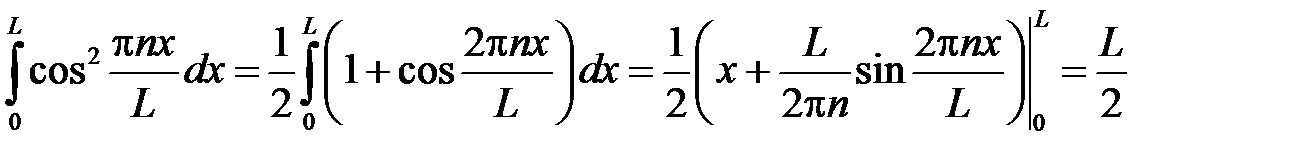 .
.
Тогда начальное условие 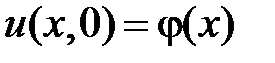 дает
дает
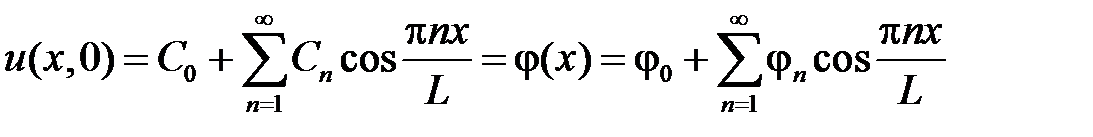 ,
,
откуда
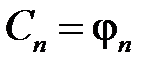 ,
, 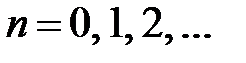 .
.
Тогда решением задачи является ряд
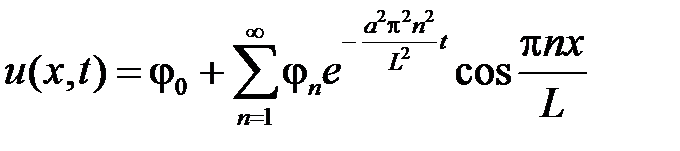 .
.
2. Теорема. Если 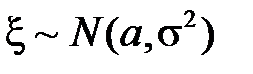 , то
, то 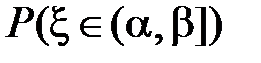 может быть вычислена по формуле
может быть вычислена по формуле
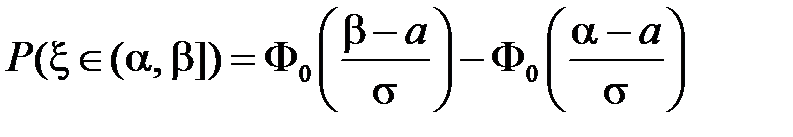 ,
,
где 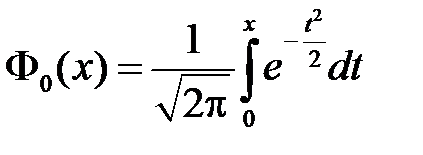 .
.
Доказательство. Если 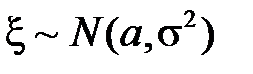 , то её плотность распределения вероятности равна
, то её плотность распределения вероятности равна
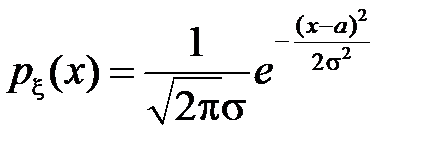 .
.
Тогда
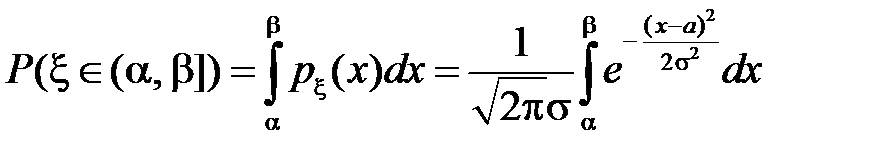 .
.
Сделаем в интеграле замену
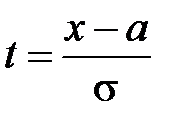 ,
, 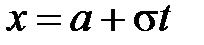 ,
, 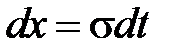 ,
, 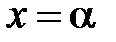
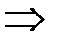
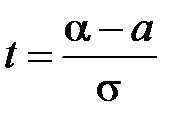 ,
, 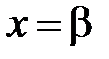
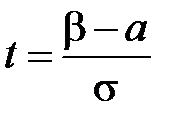 .
.
Тогда
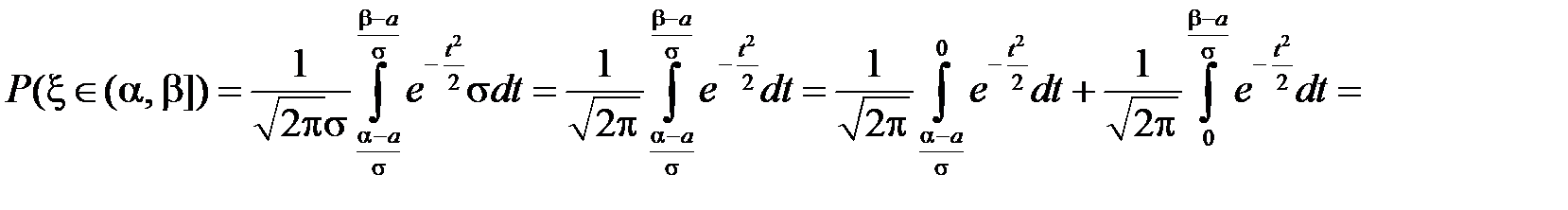
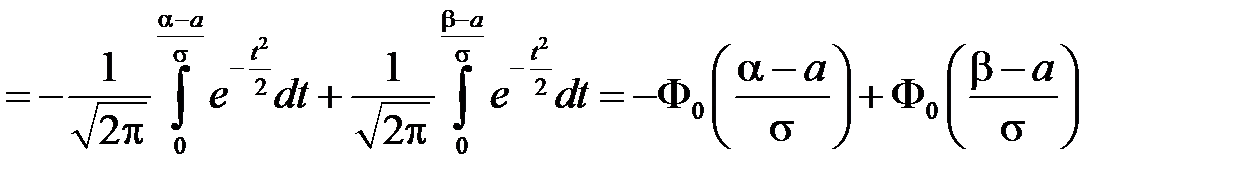 .
.
3. Решение задачи Коши для одномерного волнового уравнения на всей прямой
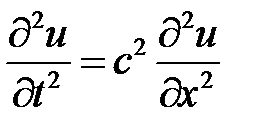 ,
, 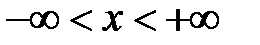 ,
, 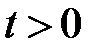 ,
,
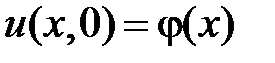 ,
, 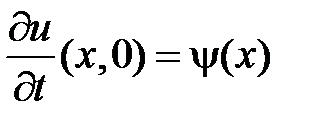 .
.
представляется формулой Даламбера
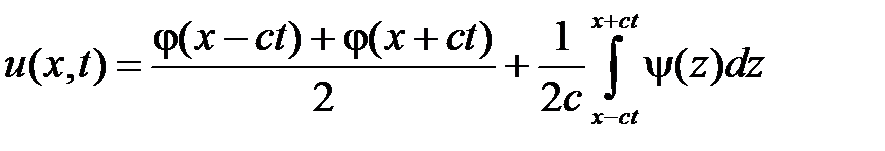 .
.
У нас 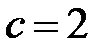 ,
, 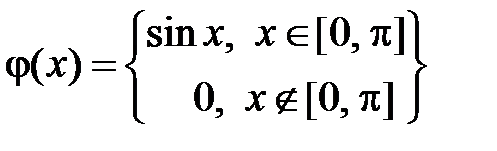 ,
, 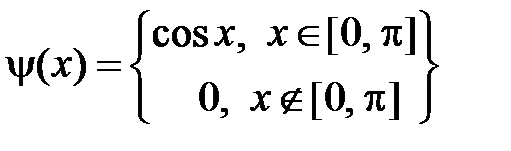 . Тогда
. Тогда
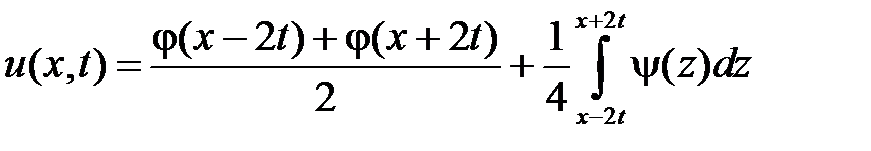 .
.
Для построения решения нарисуем на фазовой плоскости 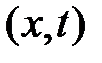 линии характеристик
линии характеристик 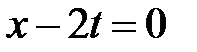 ,
, 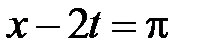 ,
, 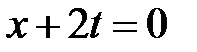 ,
, 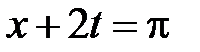 . Эти линии разбивают фазовую плоскость на шесть областей, в каждой из которых нужно найти решение.
. Эти линии разбивают фазовую плоскость на шесть областей, в каждой из которых нужно найти решение.
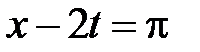
|
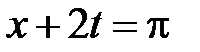
|
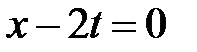
|
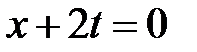
|
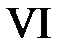
|
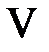
|
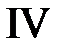
|
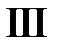
|
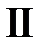
|
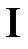
|
Область I: 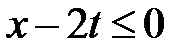 ,
, 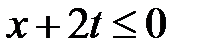 . Тогда в I
. Тогда в I 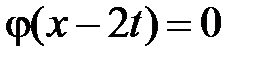 ,
, 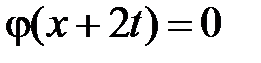 и
и 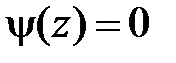 при
при 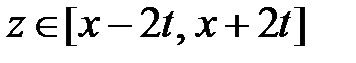 . Значит,
. Значит,
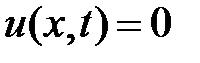 .
.
Область II: 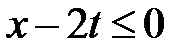 ,
, 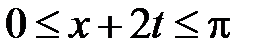 . Тогда в II
. Тогда в II 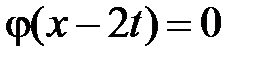 ,
, 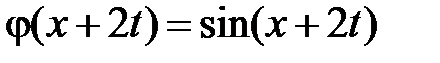 и
и 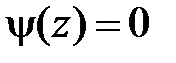 при
при 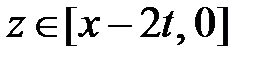 ,
, 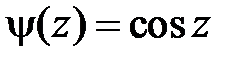 при
при 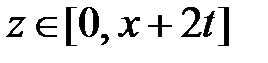 . Значит,
. Значит,
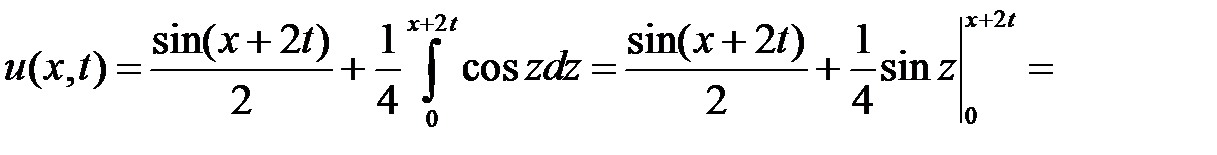
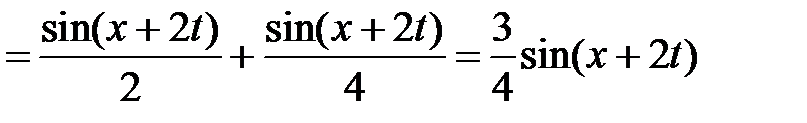 .
.
Область III: 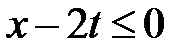 ,
, 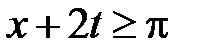 . Тогда в III
. Тогда в III 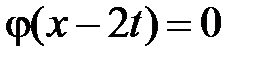 ,
, 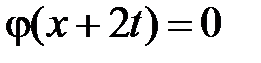 и
и 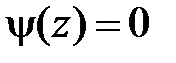 при
при 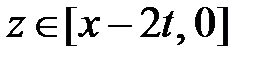 и
и 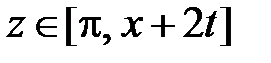 ,
, 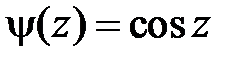 при
при 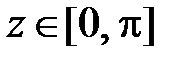 . Значит,
. Значит,
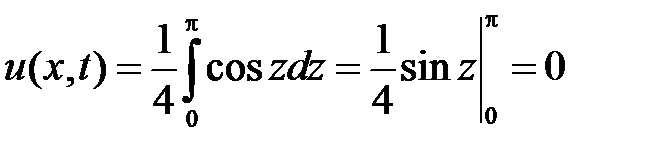 .
.
Область IV: 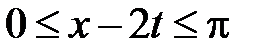 ,
, 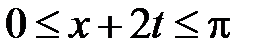 . Тогда в IV
. Тогда в IV 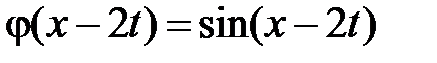 ,
, 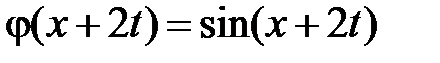 и
и 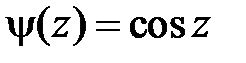 при
при 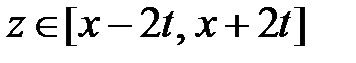 . Значит,
. Значит,
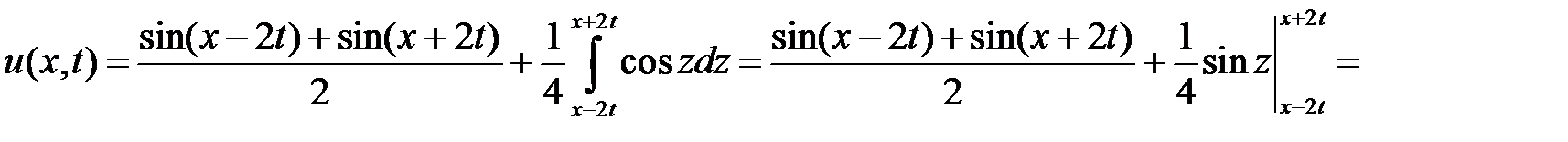
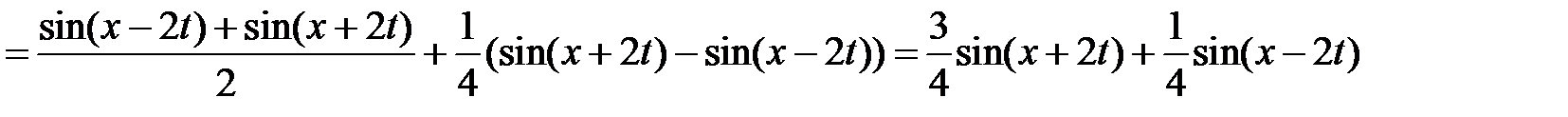 .
.
Область V: 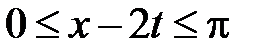 ,
, 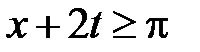 . Тогда в V
. Тогда в V 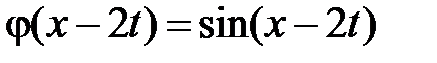 ,
, 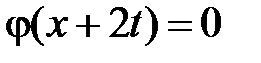 и
и 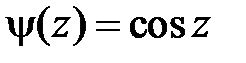 при
при 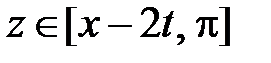 ,
, 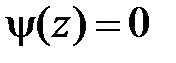 при
при 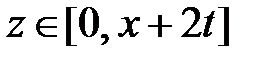 . Значит,
. Значит,
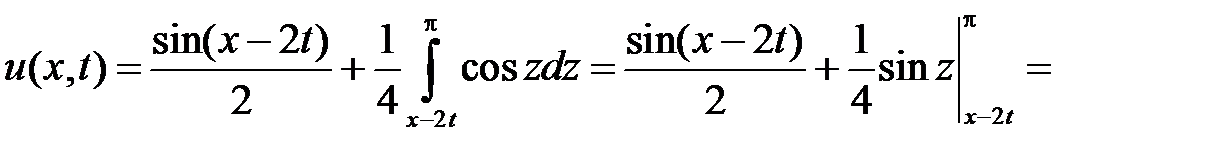
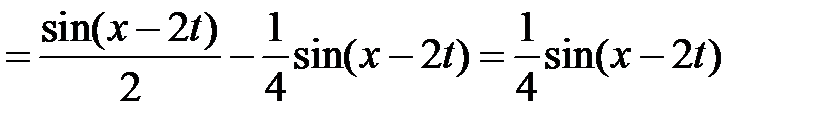 .
.
Область VI: 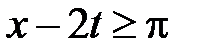 ,
, 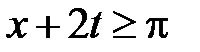 . Тогда в VI
. Тогда в VI 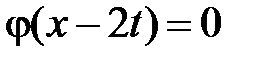 ,
, 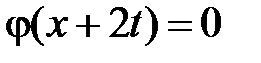 и
и 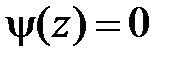 при
при 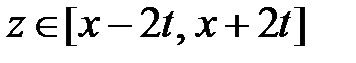 . Значит,
. Значит,
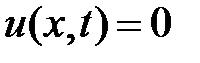 .
.
Таким образом,
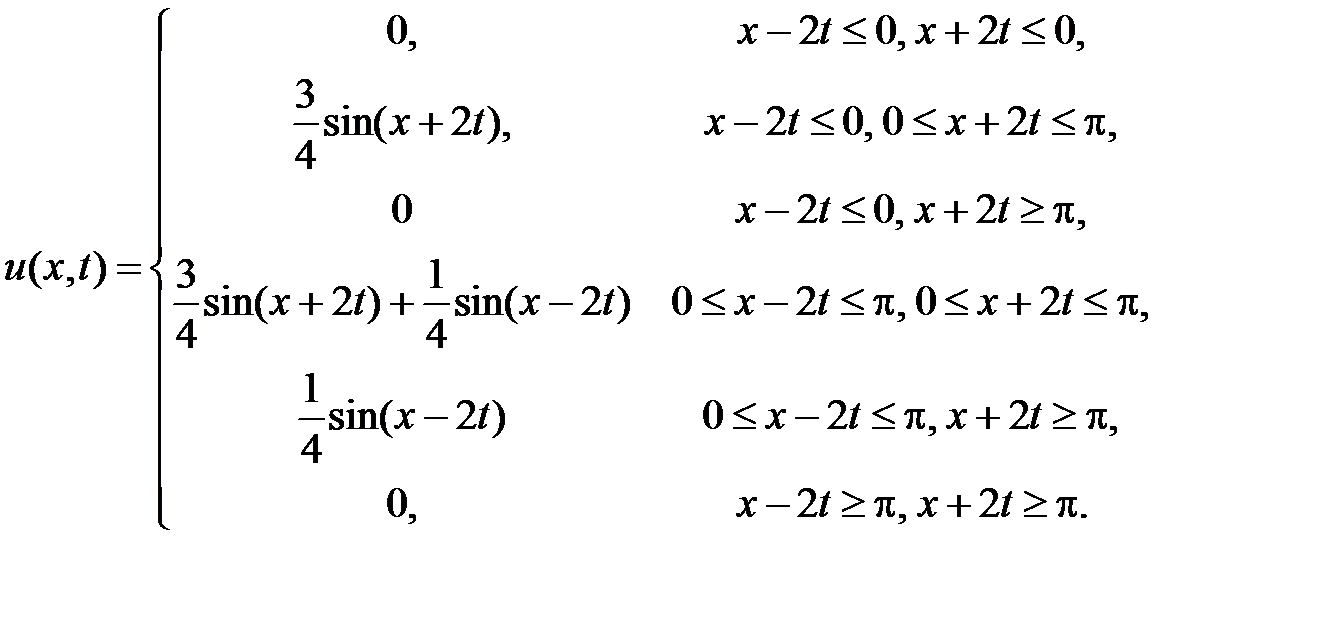
4. Введем в рассмотрение события:
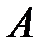 – из первого ящика достали стандартную деталь,
– из первого ящика достали стандартную деталь,
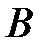 – из второго ящика достали стандартную деталь.
– из второго ящика достали стандартную деталь.
По формуле классической вероятности
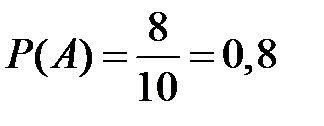 ,
, 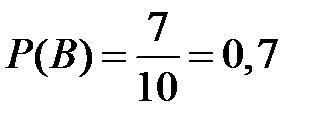 .
.
Считая события 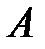 и
и 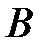 независимыми, находим вероятность того, что обе вынутые детали окажутся стандартными:
независимыми, находим вероятность того, что обе вынутые детали окажутся стандартными:
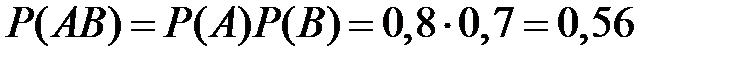 .
.
 2015-07-14
2015-07-14 408
408








