1. Уравнение теплопроводности. Задача Коши для уравнения теплопроводности на всей прямой. Формула Пуассона.
2. Дисперсия случайной величины, свойства. Вывести формулу для нахождения дисперсии случайной величины, подчиненной биномиальному закону распределения вероятностей.
3. Решить задачу Коши для неоднородного волнового уравнения
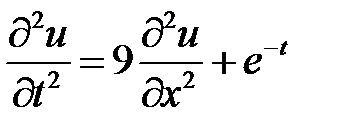 ,
, 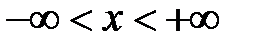 ,
, 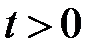 ,
,
НУ: 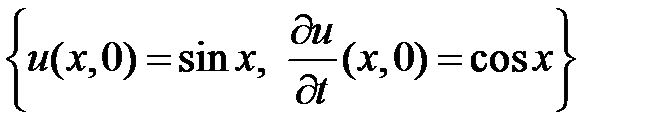 .
.
4. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами 5 см и (0,9 см)2. Найти вероятность того, что отклонение диаметра наудачу взятой детали от её математического ожидания будет меньше 2 см.
1. Уравнение теплопроводности имеет вид:
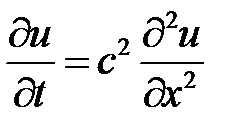 ,
,
где 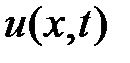 – температура тела в точке
– температура тела в точке 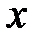 в момент времени
в момент времени 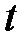 ,
, 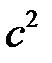 – коэффициент температуропроводности.
– коэффициент температуропроводности.
Задача Коши для уравнения теплопроводности на всей прямой имеет вид
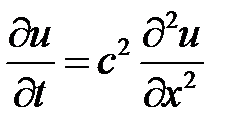 ,
, 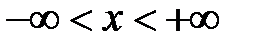 ,
,
начальное условие: 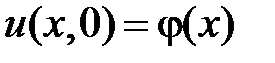 – температура в начальный момент времени.
– температура в начальный момент времени.
Получим её решение. Возьмем 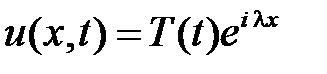 . Тогда
. Тогда
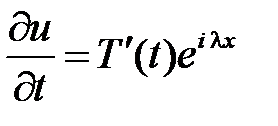 ,
, 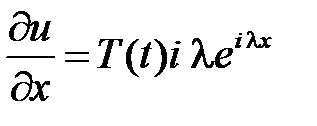 ,
, 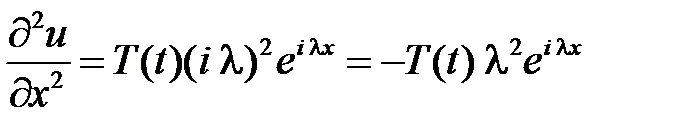 .
.
Подставив в уравнение, получим
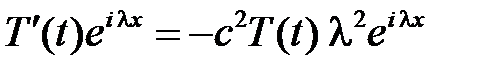 ,
,
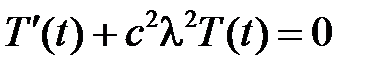 ,
,
откуда 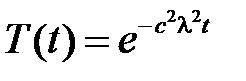 . Тогда
. Тогда
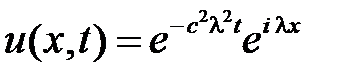 ,
,
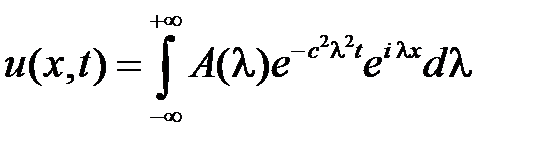 .
.
При 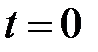 получим
получим
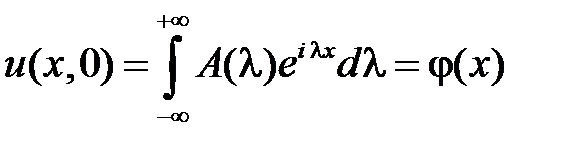 .
.
С помощью обратного преобразования Фурье
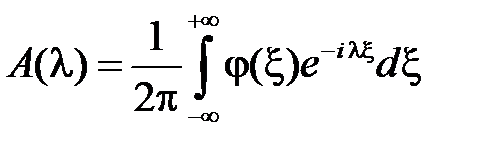 .
.
Тогда
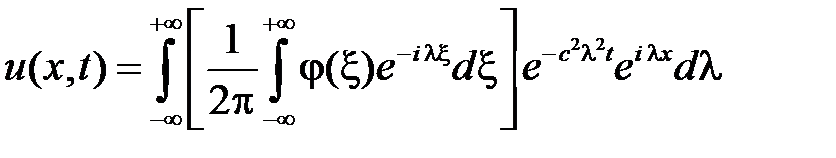 .
.
Меняя порядок интегрирования, получим
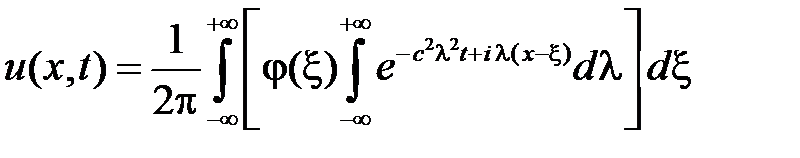
Приведем экспоненту к виду 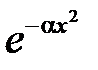 :
:
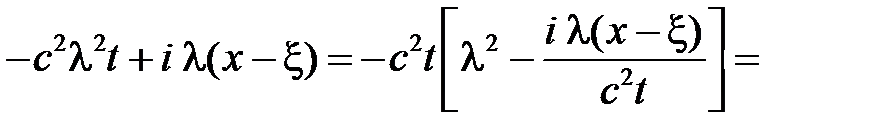
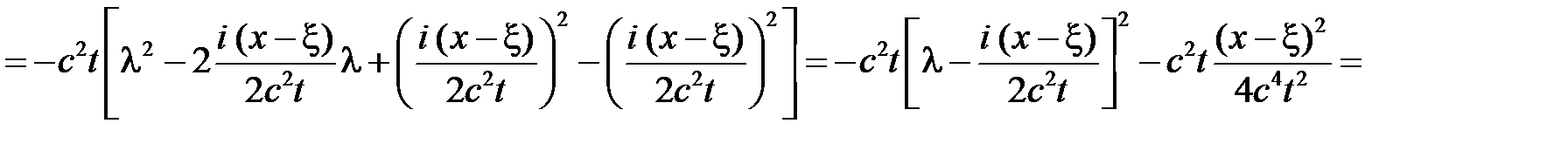
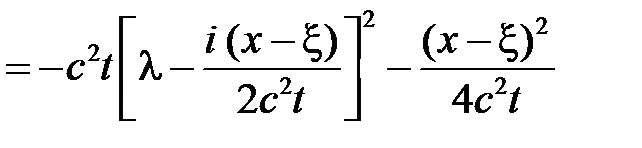 .
.
Тогда
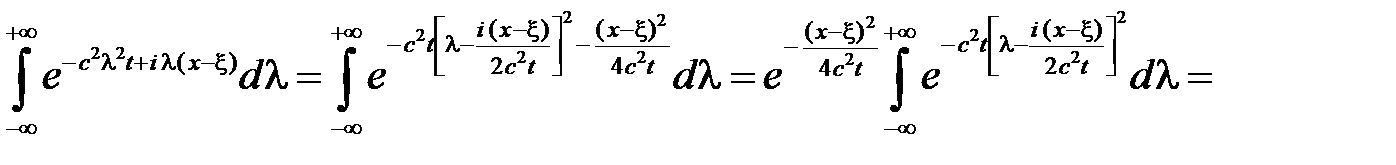
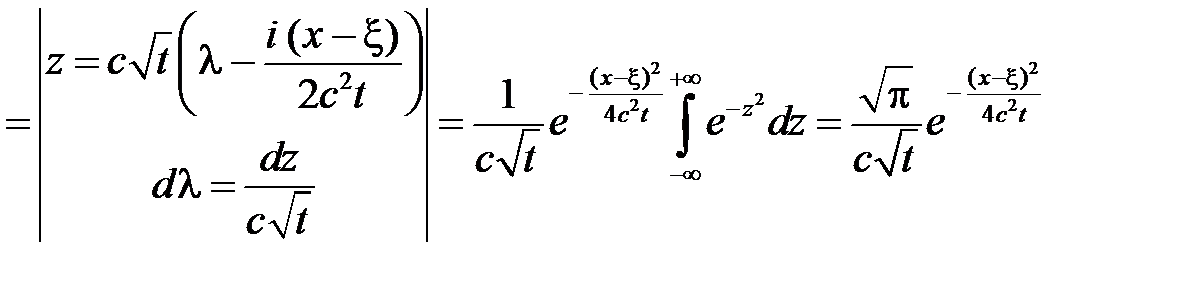 ,
,
так как
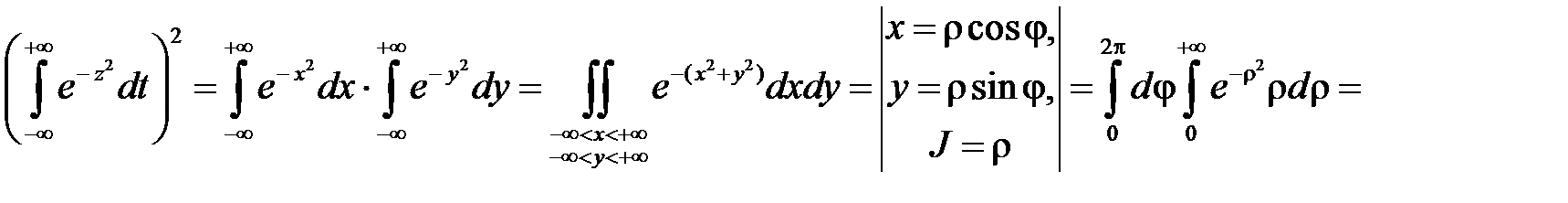
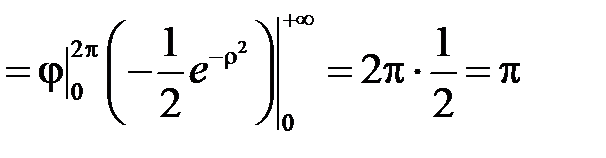 .
.
Значит,
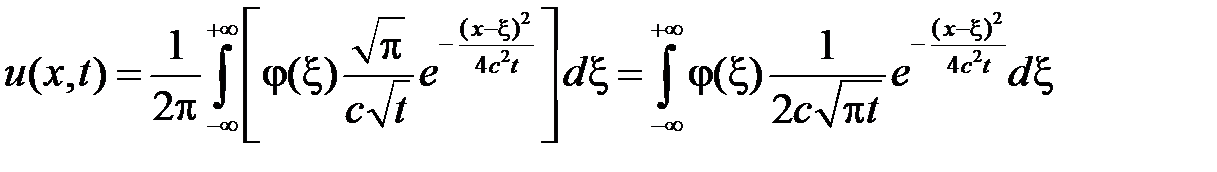 .
.
Обозначим
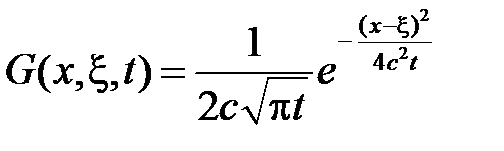 .
.
Тогда получим формулу Пуассона, которая дает решение задачи Коши для уравнения теплопроводности на всей прямой:
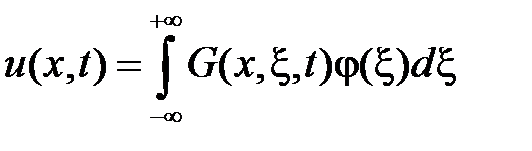 .
.
2. Определение. Дисперсией 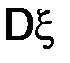 случайной величины
случайной величины 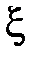 называется математическое ожидание квадрата отклонения от
называется математическое ожидание квадрата отклонения от 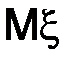 :
:
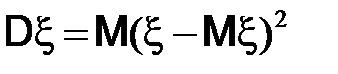 .
.
Дисперсия служит мерой рассеяния значений случайной величины около среднего значения (математического ожидания).
Свойства дисперсии:
1) 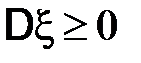 ;
;
2) 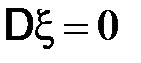 тогда и только тогда, когда
тогда и только тогда, когда 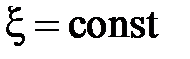 ;
;
3) 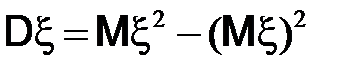 ;
;
4) для любых 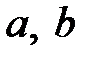
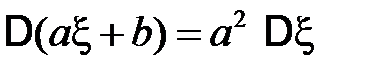 ;
;
5) если случайные величины 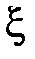 и
и 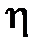 независимы, то
независимы, то 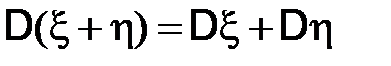 .
.
Докажем свойство 3):
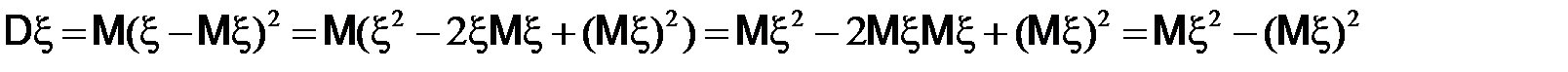 .
.
Для дискретных и непрерывных случайных величин дисперсия вычисляется соответственно по формулам:
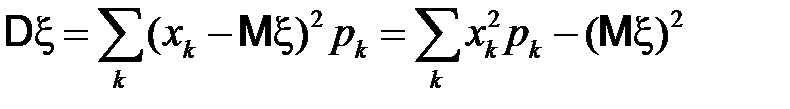 ,
,
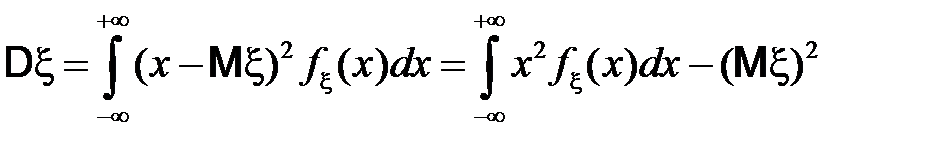 .
.
Найдем дисперсию биномиального распределения. Пусть случайная величина 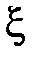 имеет биномиальное распределение, т.е. она принимает значения от 0 до
имеет биномиальное распределение, т.е. она принимает значения от 0 до 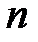 с вероятностями
с вероятностями
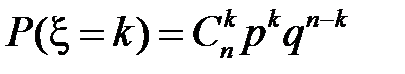 ,
, 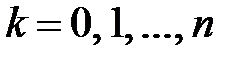 ,
,
и является числом успехов в 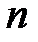 испытаниях по схеме Бернулли с вероятностью успеха
испытаниях по схеме Бернулли с вероятностью успеха 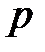 ,
, 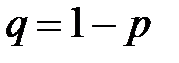 . Рассмотрим
. Рассмотрим 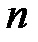 бернуллиевых случайных величин
бернуллиевых случайных величин 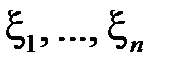 , которые принимают два значения: 1 с вероятностью
, которые принимают два значения: 1 с вероятностью 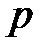 , если соответствующее испытание закончилось успехом, и 0 с вероятностью
, если соответствующее испытание закончилось успехом, и 0 с вероятностью 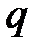 в противном случае. Тогда
в противном случае. Тогда
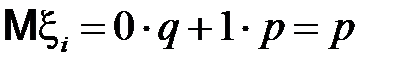 ,
, 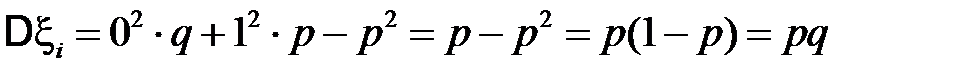 ,
, 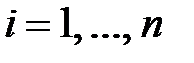 .
.
Кроме того, 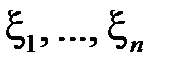 независимы и
независимы и 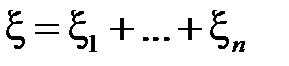 . Значит, по свойству 5) дисперсии дисперсия биномиального распределения равна
. Значит, по свойству 5) дисперсии дисперсия биномиального распределения равна
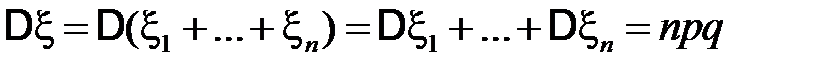 .
.
3. Решение задачи Коши для неоднородного волнового уравнения
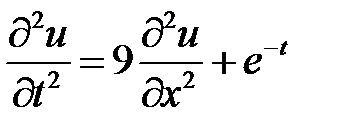 ,
, 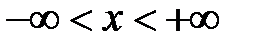 ,
, 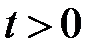 ,
,
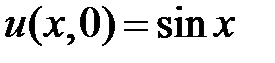 ,
, 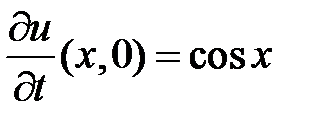 ,
,
будем искать в виде
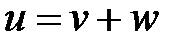 ,
,
где 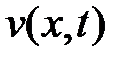 – решение задачи
– решение задачи
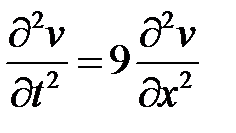 ,
, 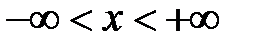 ,
, 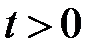 ,
,
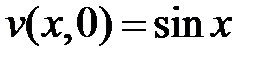 ,
, 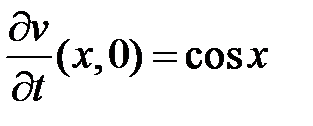 ,
,
а 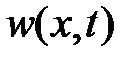 – решение задачи
– решение задачи
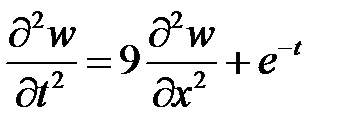 ,
, 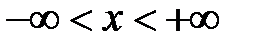 ,
, 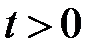 ,
,
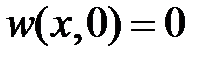 ,
, 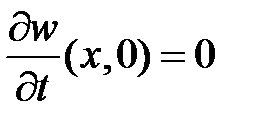 .
.
Функцию 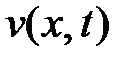 находим по формуле Даламбера
находим по формуле Даламбера
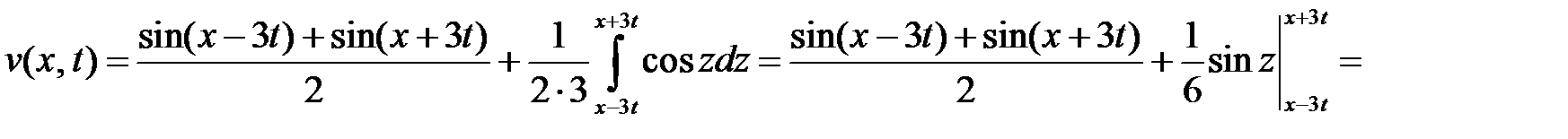
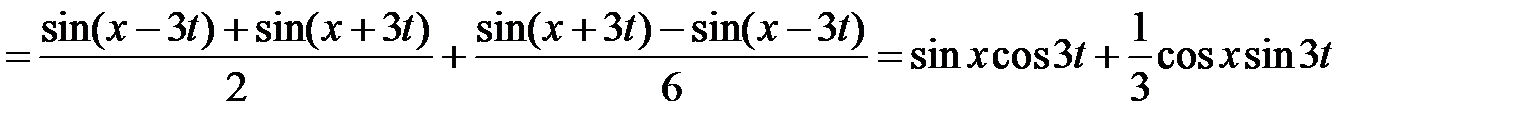 .
.
Функция 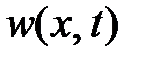 находится по формуле
находится по формуле
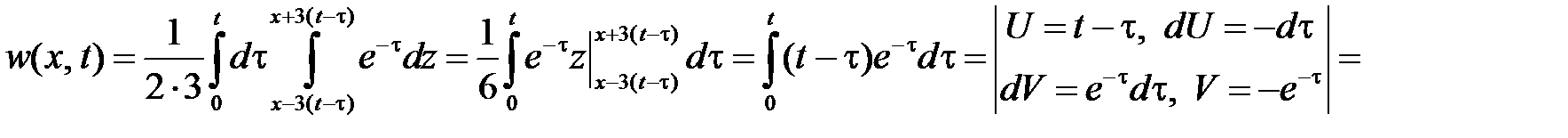
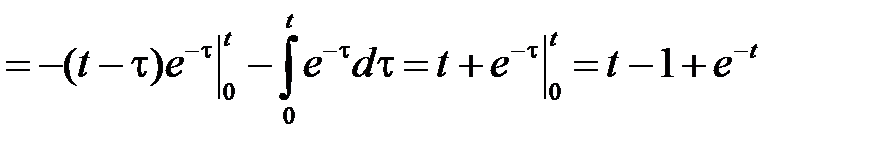 .
.
Тогда
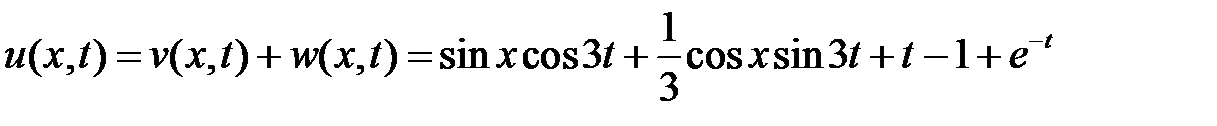 .
.
4. Для расчета вероятностей попадания нормальной случайной величины 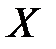 с математическим ожиданием
с математическим ожиданием 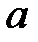 и среднеквадратическим отклонением
и среднеквадратическим отклонением  в промежуток
в промежуток 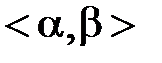 используется формула
используется формула
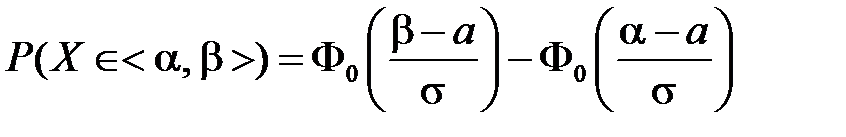 ,
,
где 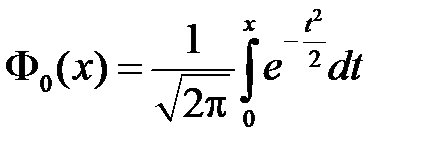 , причем
, причем 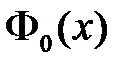 – нечетная функция:
– нечетная функция: 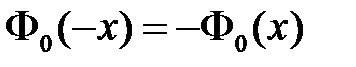 .
.
Пусть случайная величина 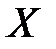 – размер диаметра детали. При
– размер диаметра детали. При 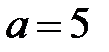 ,
, 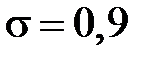 получим
получим
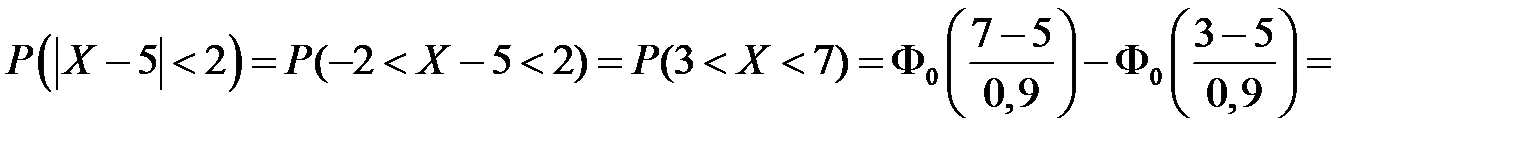
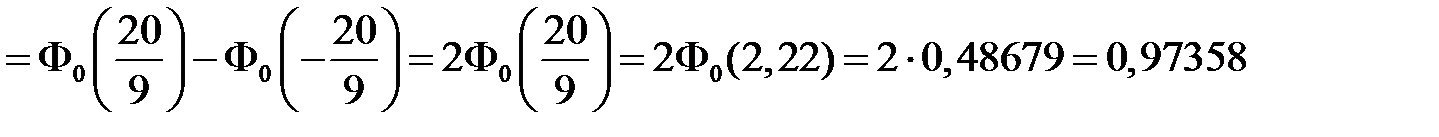 .
.
 2015-07-14
2015-07-14 410
410








