1. Смешанная задача для однородного волнового уравнения на отрезке 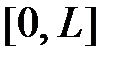 при нулевых граничных условиях
при нулевых граничных условиях 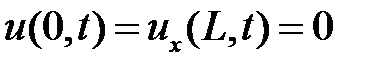 .
.
2. Нормальный закон распределения. Доказать, что, если 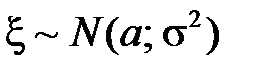 , то
, то 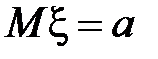 .
.
3. Найти решение смешанной задачи для волнового уравнения на полупрямой
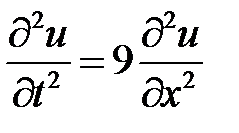 ,
, 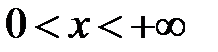 ,
,
ГУ: 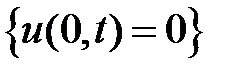 ;
;
НУ: 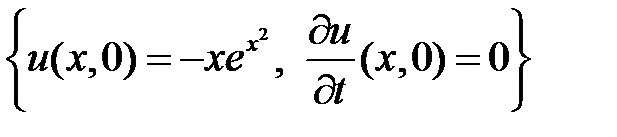 .
.
4. Из 100 лампочек 20 изготовлены на первом заводе, 30 на втором, а остальные на третьем. Первый завод выпускает 1% брака, второй – 0,5%; третий – 0,6%. Какова вероятность того, что наудачу взятая лампочка окажется бракованной?
1. Смешанная задача для однородного волнового уравнения на отрезке 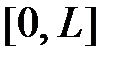 при нулевых граничных условиях имеет вид:
при нулевых граничных условиях имеет вид:
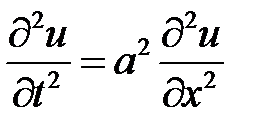 ,
, 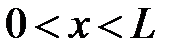 ,
, 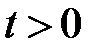 ,
,
граничные условия: 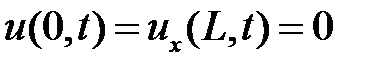 ;
;
начальные условия: 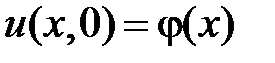 ,
, 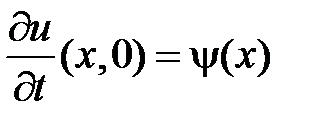 .
.
Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 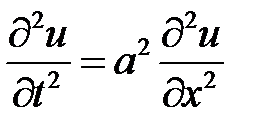 будем искать в виде
будем искать в виде 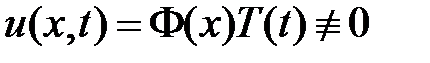 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
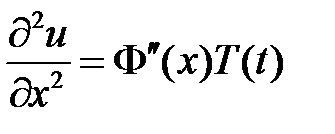 ,
, 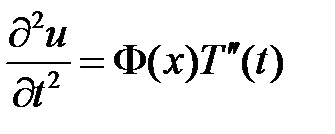 ,
,
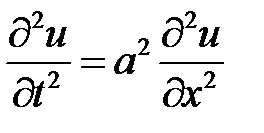 :
: 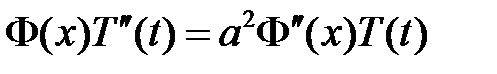 ,
,
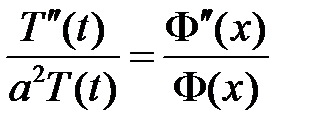 ,
, 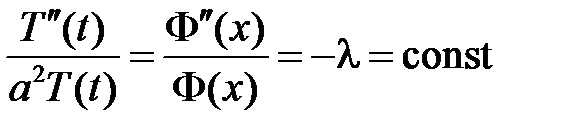 ,
, 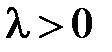 .
.
Тогда функции 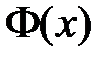 и
и 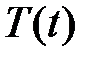 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 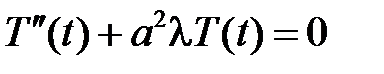 .
.
Из граничных условий 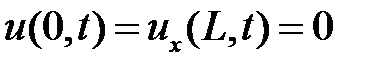 получаем краевые условия для функции
получаем краевые условия для функции 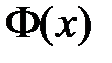 :
: 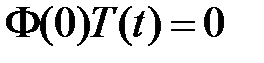 ,
, 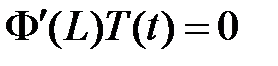 , значит,
, значит, 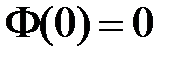 ,
, 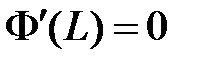 . Таким образом, для определения
. Таким образом, для определения 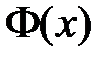 и
и 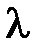 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

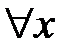 :
: 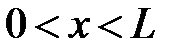 ,
,
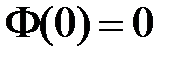 ,
, 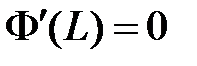 .
.
При 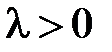 (при
(при 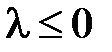 задача имеет только тривиальные решения) общее решение уравнения
задача имеет только тривиальные решения) общее решение уравнения  имеет вид
имеет вид
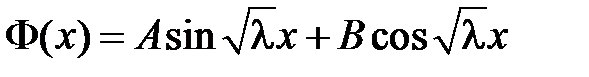 .
.
Из краевого условия 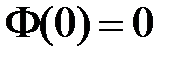 получаем:
получаем: 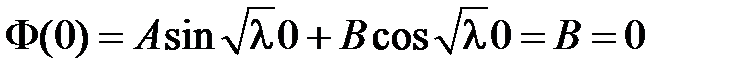 ,
, 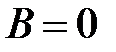 , т.е.
, т.е. 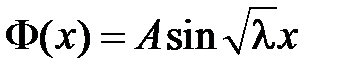 и
и 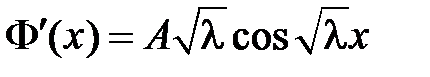 .
.
Из краевого условия 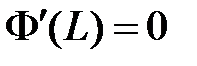 получаем:
получаем: 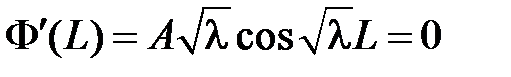 . Поскольку
. Поскольку 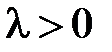 и
и 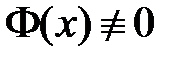 , то
, то 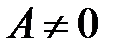 и равенство
и равенство 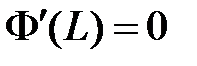 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 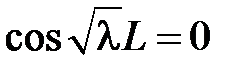 , откуда получаем
, откуда получаем 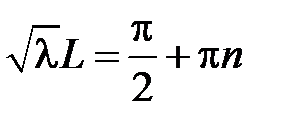 ,
, 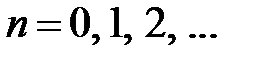 , т.е.
, т.е. 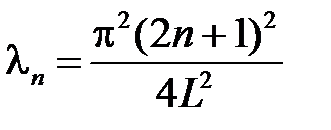 ,
, 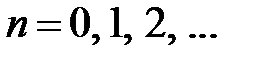 . Тогда получим
. Тогда получим 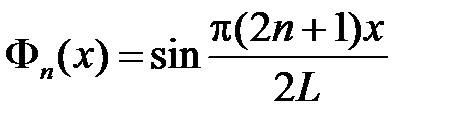 ,
, 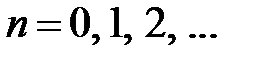 . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 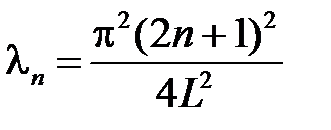 ,
, 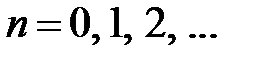 ;
;
собственные функции 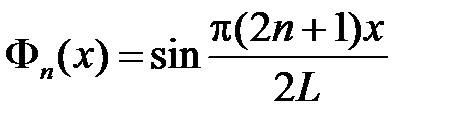 ,
, 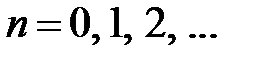 .
.
Теперь при каждом 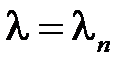 решаем уравнение для
решаем уравнение для 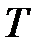 :
:
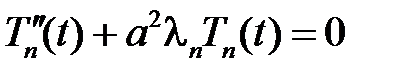 ,
, 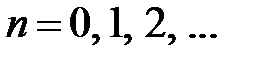 .
.
Общее решение этого уравнения имеет вид
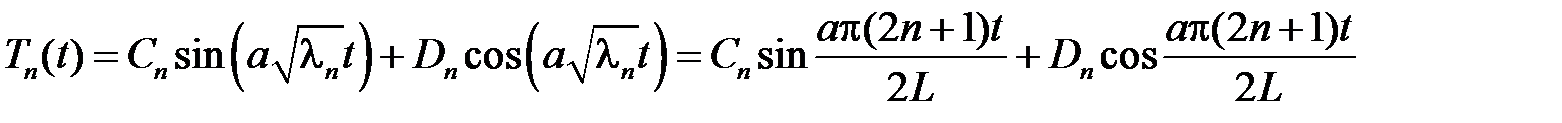 .
.
Тогда
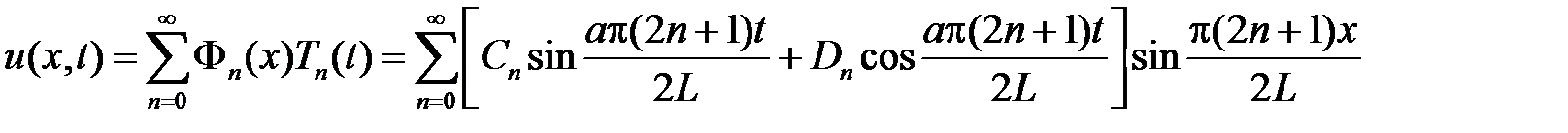 .
.
Для нахождения коэффициентов 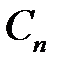 ,
, 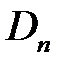 ,
, 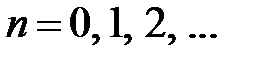 , воспользуемся начальными условиями
, воспользуемся начальными условиями 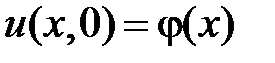 ,
, 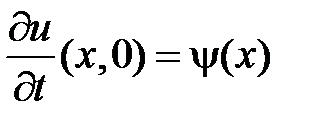 .
.
Разложим функции 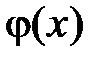 и
и 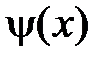 на отрезке
на отрезке 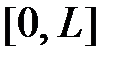 в ряды Фурье по системе
в ряды Фурье по системе 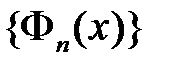 :
:
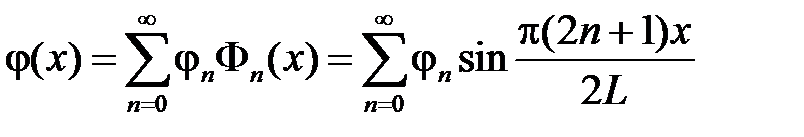 ,
,
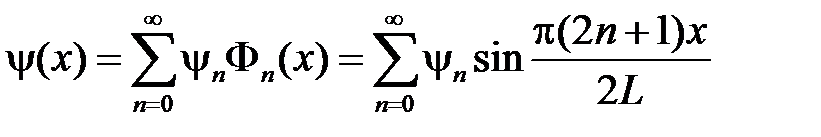 ,
,
где
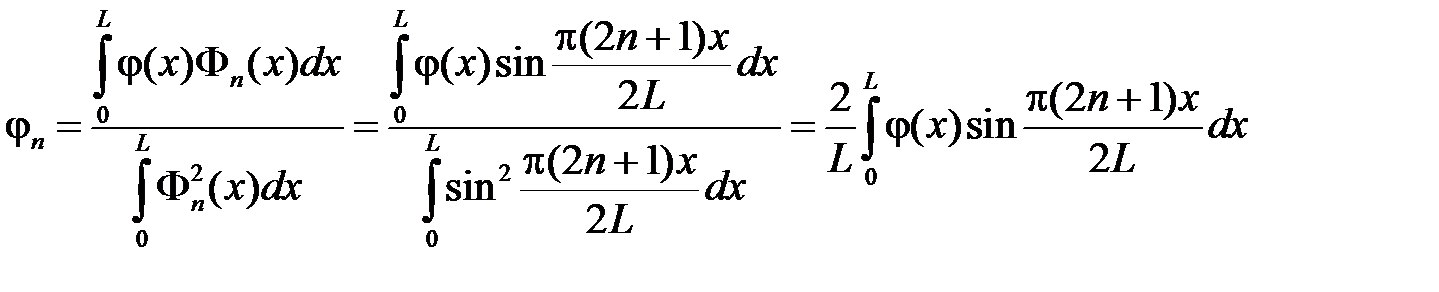 ,
,
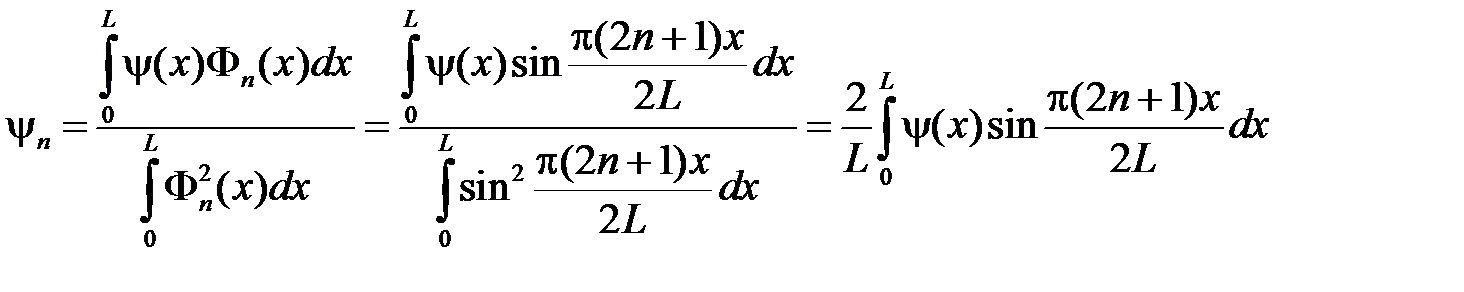 ,
,
так как
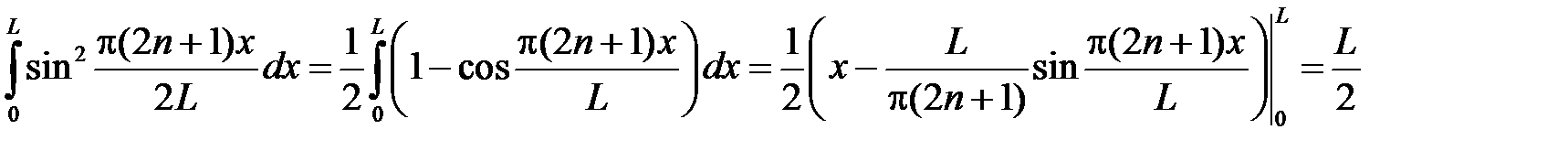 .
.
Тогда начальное условие 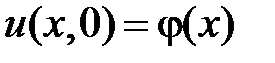 дает
дает
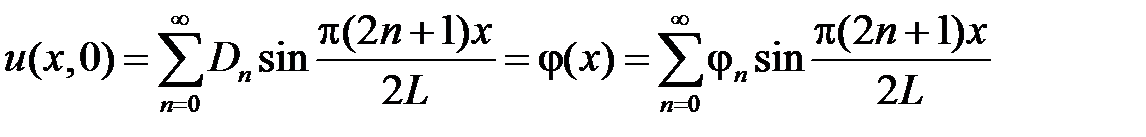 ,
,
откуда
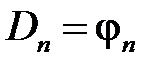 ,
, 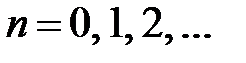 .
.
Находим 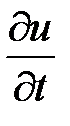 :
:
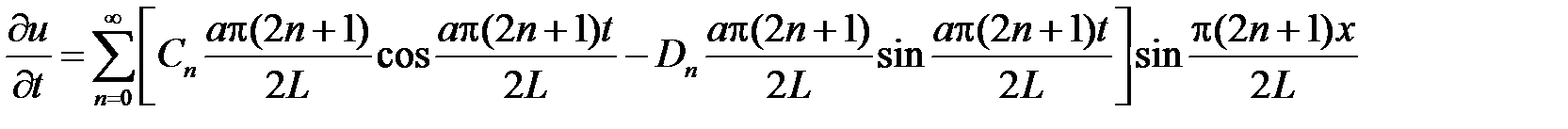 .
.
Тогда начальное условие 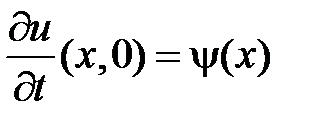 дает
дает
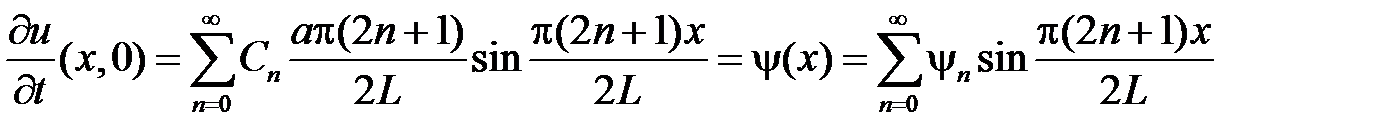 ,
,
откуда
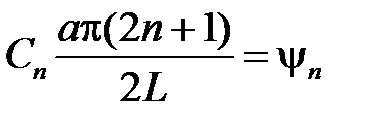 ,
, 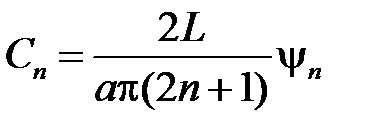 ,
,  .
.
Тогда решением задачи является ряд
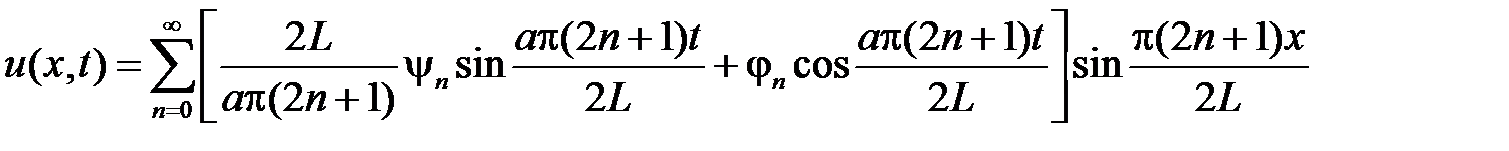 .
.
2. Нормальным распределением с параметрами 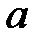 ,
, 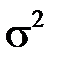 называется распределение вероятностей с плотностью (
называется распределение вероятностей с плотностью (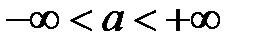 ,
, 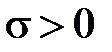 )
)
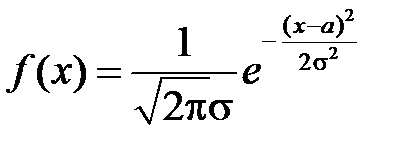 ,
, 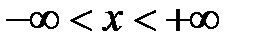 .
.
Математическое ожидание непрерывной случайной величины 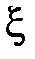 находится по формуле
находится по формуле
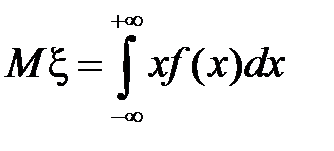 .
.
Для нормального закона
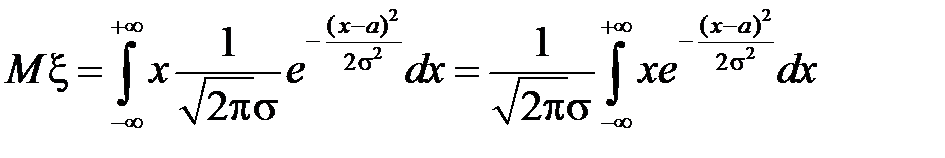 .
.
Сделаем в интеграле замену 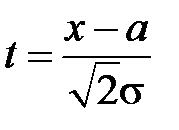 , откуда
, откуда 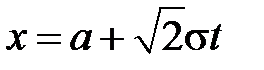 ,
, 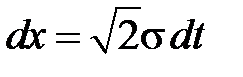 , если
, если 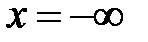 , то
, то 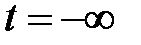 , если
, если 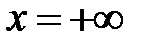 , то
, то 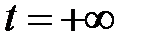 . Тогда
. Тогда
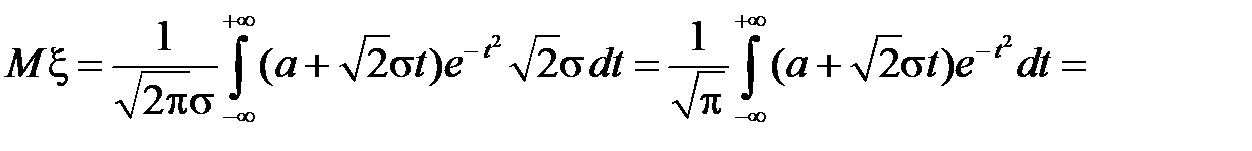
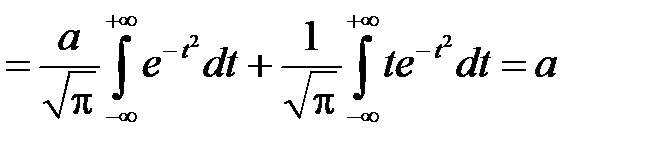 ,
,
так как
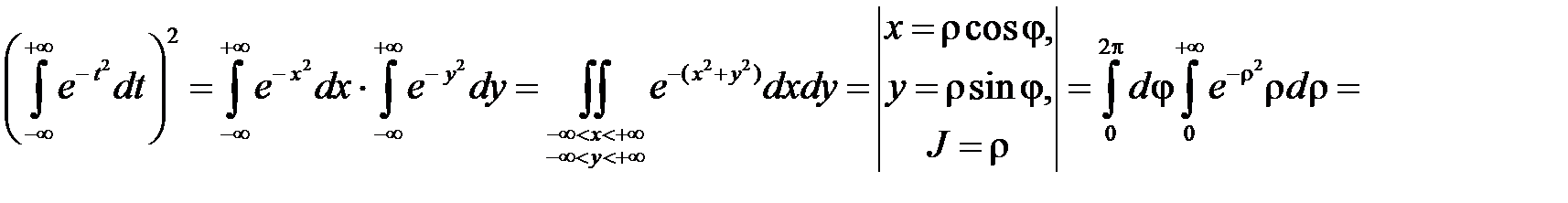
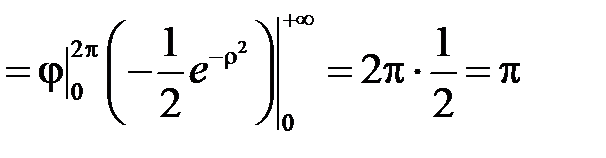 ,
,
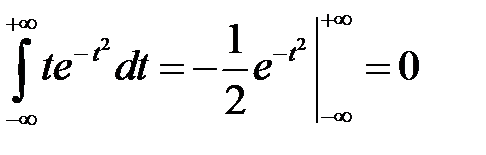 .
.
3. Для смешанной задачи для волнового уравнения на полупрямой
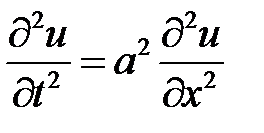 ,
,  ,
,  ,
,
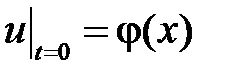 ,
, 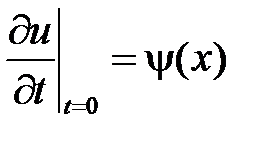 ,
, 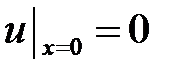 .
.
решение записывается по формуле Даламбера
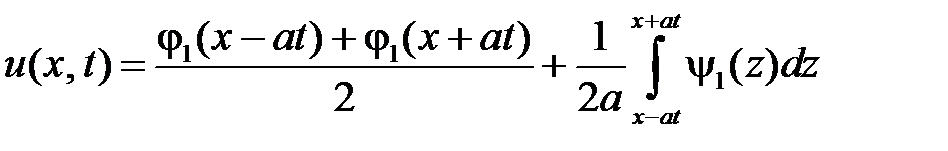 ,
,
где 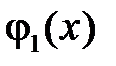 ,
, 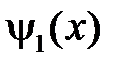 продолженные нечётным образом на отрицательную часть оси
продолженные нечётным образом на отрицательную часть оси 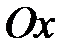 функции
функции 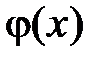 и
и 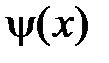 соответственно, то есть:
соответственно, то есть:
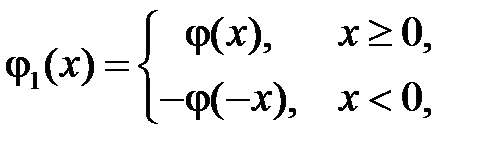
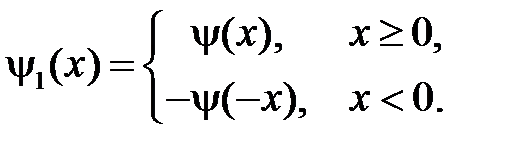
У нас 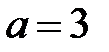 ,
, 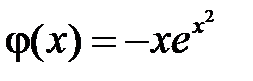 ,
, 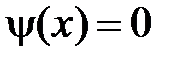 . Тогда
. Тогда
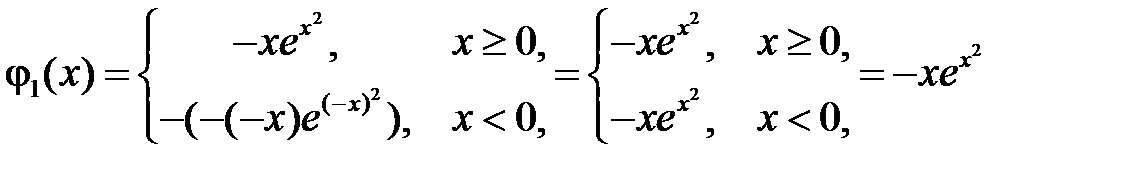 ,
, 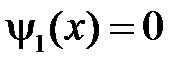
и решение задачи имеет вид
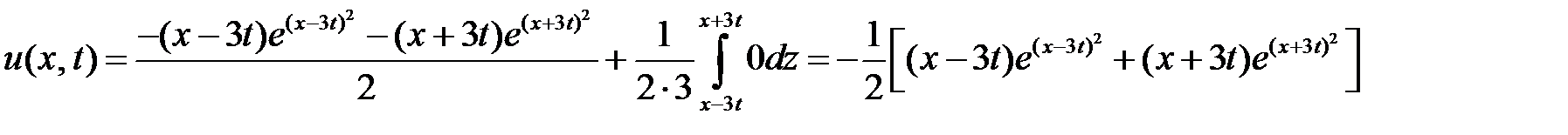 .
.
4. Воспользуемся формулой полной вероятности. Событие
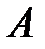 – наудачу взятая лампочка оказалась бракованной.
– наудачу взятая лампочка оказалась бракованной.
Введем гипотезы:
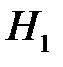 – лампочка произведена на первом заводе;
– лампочка произведена на первом заводе;
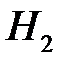 – лампочка произведена на втором заводе;
– лампочка произведена на втором заводе;
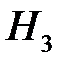 – лампочка произведена на третьем заводе.
– лампочка произведена на третьем заводе.
Поскольку всего изготовлено 100 лампочек, то вероятности гипотез
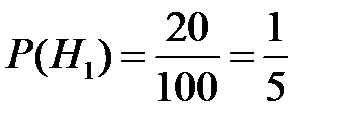 ,
, 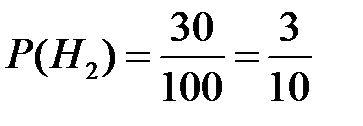 ,
, 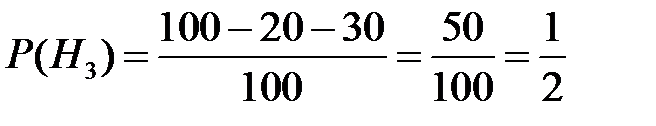 .
.
Условные вероятности 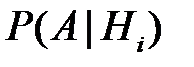 ,
, 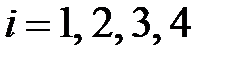 , по условию равны
, по условию равны
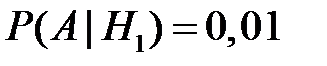 ,
, 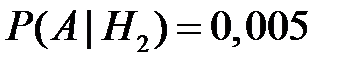 ,
, 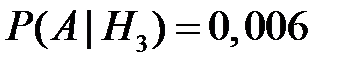 .
.
Тогда по формуле полной вероятности
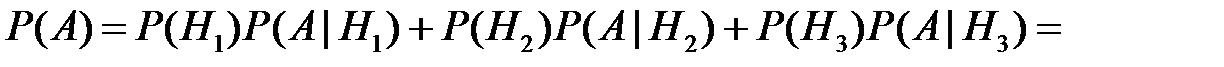
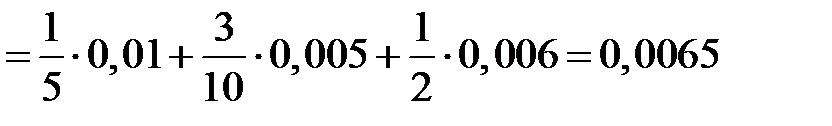 .
.
 2015-07-14
2015-07-14 367
367








