1. Смешанная задача для однородного уравнения теплопроводности на отрезке 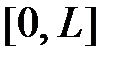 при нулевых граничных условиях
при нулевых граничных условиях 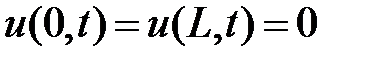 .
.
2. Математическое ожидание случайной величины, его свойства. Вывести формулу для нахождения математического ожидания случайной величины, подчиненной биномиальному закону распределения вероятностей.
3. Решить задачу Неймана для уравнения Лапласа 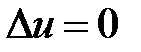 вне круга радиуса
вне круга радиуса 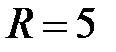 . ГУ:
. ГУ: 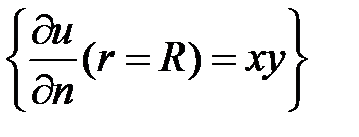 .
.
4. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найти вероятность того, что взятая наудачу деталь из наудачу взятого набора является стандартной.
1. Смешанная задача для однородного уравнения теплопроводности на отрезке 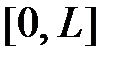 при нулевых граничных условиях имеет вид:
при нулевых граничных условиях имеет вид:
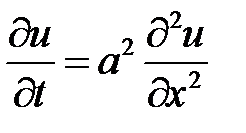 ,
, 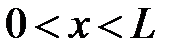 ,
, 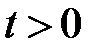 ,
,
граничные условия: 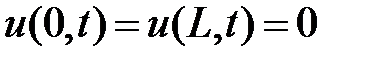 ;
;
начальное условие: 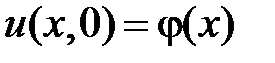 .
.
Для решения задачи воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 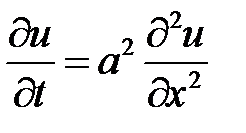 будем искать в виде
будем искать в виде 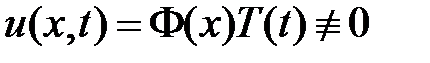 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
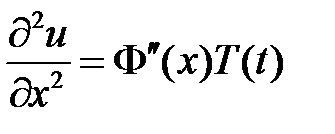 ,
, 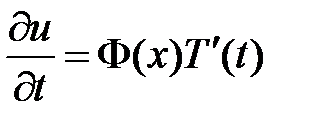
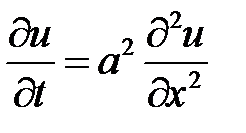 :
: 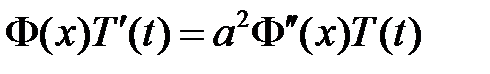 ,
,
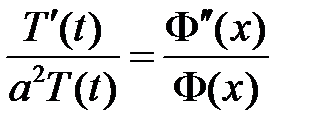 ,
, 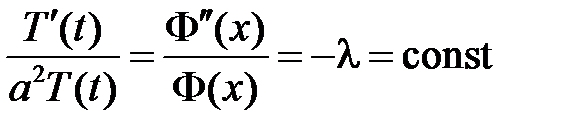 ,
, 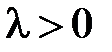 .
.
Тогда функции 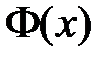 и
и 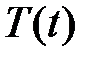 являются соответственно решениями уравнений
являются соответственно решениями уравнений
 ,
, 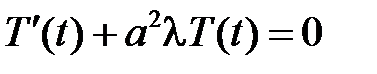 .
.
Из граничных условий 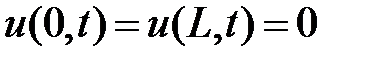 получаем краевые условия для функции
получаем краевые условия для функции 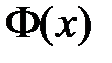 :
: 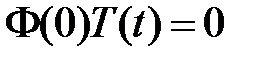 ,
, 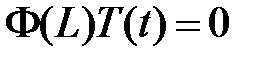 , значит,
, значит, 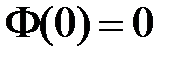 ,
, 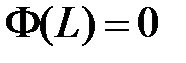 . Таким образом, для определения
. Таким образом, для определения 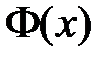 и
и 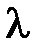 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

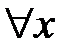 :
: 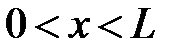 ,
,
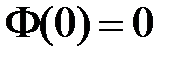 ,
, 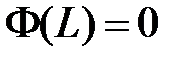 .
.
Поскольку 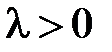 (при
(при 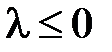 задача имеет только тривиальные решения), то общее решение уравнения
задача имеет только тривиальные решения), то общее решение уравнения  имеет вид
имеет вид
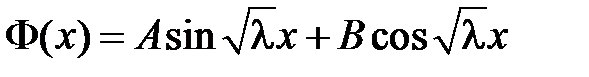 .
.
Из краевого условия 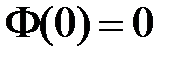 получаем:
получаем: 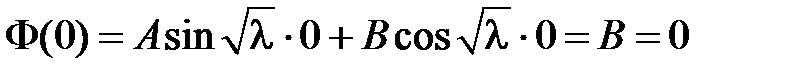 , т.е.
, т.е. 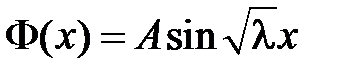 .
.
Из краевого условия 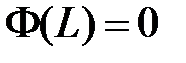 получаем:
получаем: 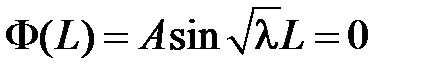 . Поскольку
. Поскольку 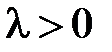 и
и 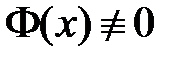 , то
, то 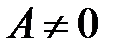 и равенство
и равенство 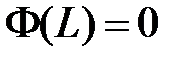 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 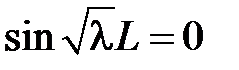 , откуда получаем
, откуда получаем 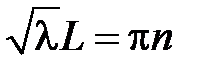 ,
,  , т.е.
, т.е. 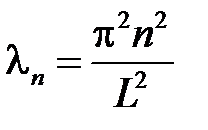 ,
,  . Тогда получим
. Тогда получим 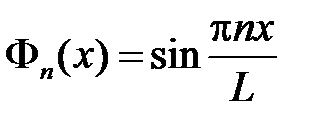 ,
,  . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 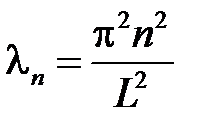 ,
,  ;
;
собственные функции 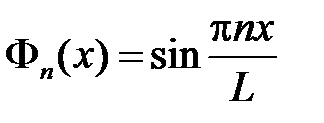 ,
,  .
.
Теперь при каждом 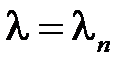 решаем уравнение для
решаем уравнение для 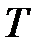 :
:
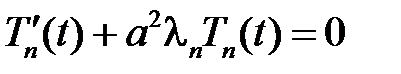 ,
,  .
.
Общее решение этого уравнения имеет вид
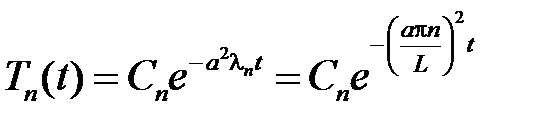 .
.
Тогда
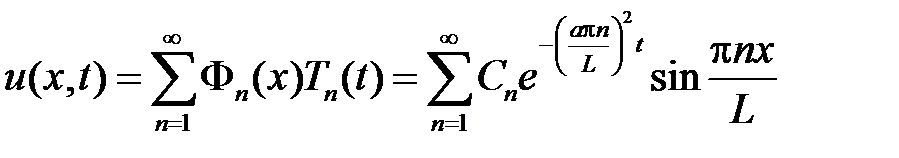 .
.
Для нахождения коэффициентов 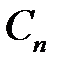 ,
,  , воспользуемся начальным условием
, воспользуемся начальным условием 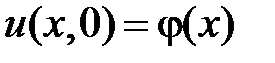 .
.
Разложим функции 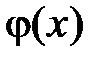 на отрезке
на отрезке 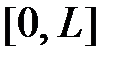 в ряд Фурье по системе
в ряд Фурье по системе 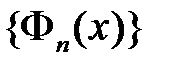 :
:
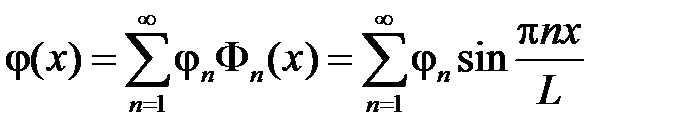 ,
,
где
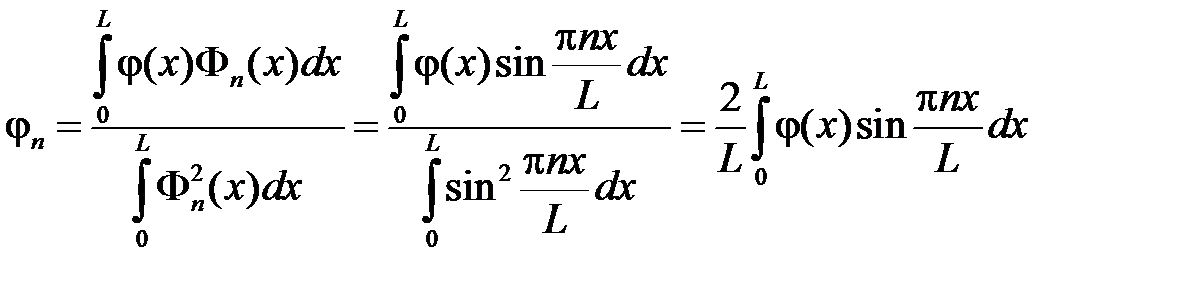 ,
,
так как 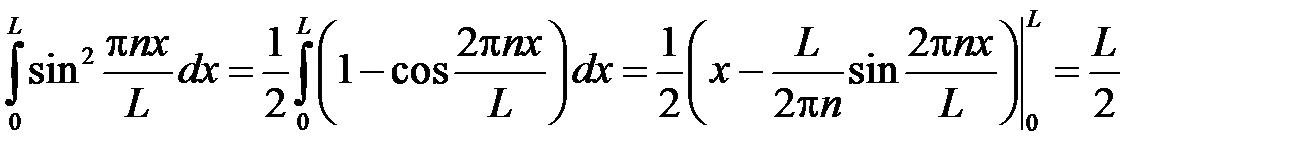 .
.
Тогда начальное условие 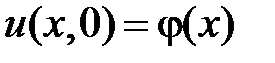 дает
дает
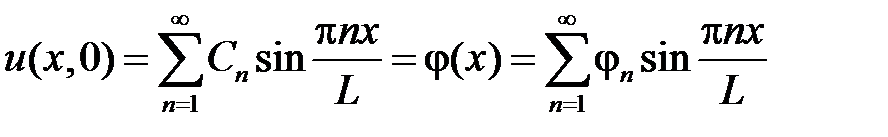 ,
,
откуда
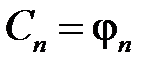 ,
, 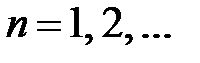 .
.
Тогда решением задачи является ряд
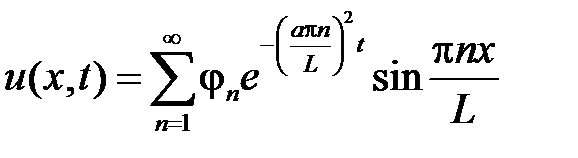 .
.
2. Определение. Математическим ожиданием дискретной случайной величины 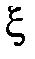 , принимающей значения
, принимающей значения 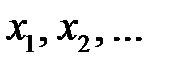 с вероятностями
с вероятностями 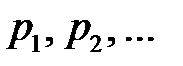 , называется ряд (в предположении, что он абсолютно сходится)
, называется ряд (в предположении, что он абсолютно сходится)
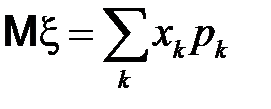 .
.
Математическим ожиданием непрерывной случайной величины 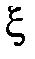 с плотностью
с плотностью 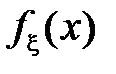 , называется интеграл (в предположении, что он абсолютно сходится)
, называется интеграл (в предположении, что он абсолютно сходится)
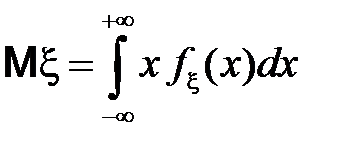 .
.
Математическое ожидание показывает какое значение в среднем принимает случайная величина.
Свойства математического ожидания:
1) 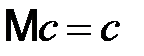 ,
, 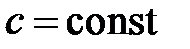 ;
;
2) 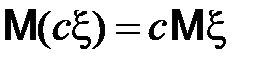
3) 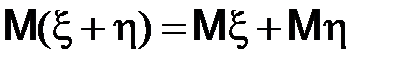 ;
;
4) если случайные величины 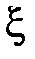 и
и 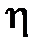 независимы, то
независимы, то 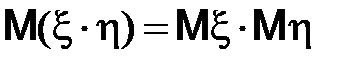 .
.
Найдем математическое ожидание биномиального распределения. Пусть случайная величина 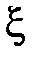 имеет биномиальное распределение, т.е. она принимает значения от 0 до
имеет биномиальное распределение, т.е. она принимает значения от 0 до 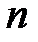 с вероятностями
с вероятностями
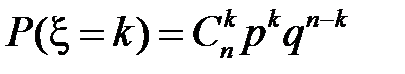 ,
, 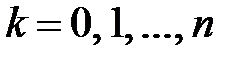 ,
,
и является числом успехов в 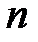 испытаниях по схеме Бернулли с вероятностью успеха
испытаниях по схеме Бернулли с вероятностью успеха 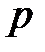 ,
, 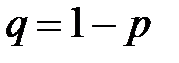 . Рассмотрим
. Рассмотрим 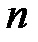 бернуллиевых случайных величин
бернуллиевых случайных величин 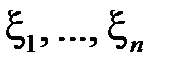 , которые принимают два значения: 1 с вероятностью
, которые принимают два значения: 1 с вероятностью 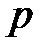 , если соответствующее испытание закончилось успехом, и 0 с вероятностью
, если соответствующее испытание закончилось успехом, и 0 с вероятностью 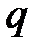 в противном случае. Тогда
в противном случае. Тогда
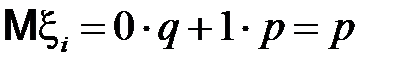 ,
, 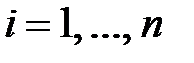 .
.
Кроме того, 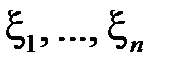 независимы и
независимы и 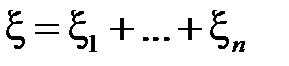 . Значит, по свойству 3) математического ожидания для биномиального распределения получим
. Значит, по свойству 3) математического ожидания для биномиального распределения получим
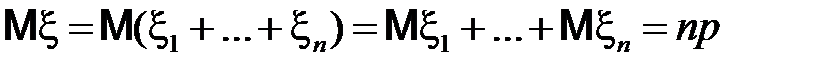 .
.
3. Внешняя задача Неймана для уравнения Лапласа вне круга радиуса 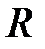 ставится следующим образом:
ставится следующим образом:
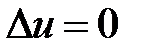 при
при 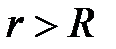 ,
,
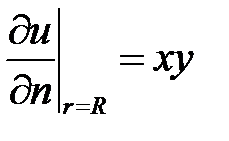 ,
,
где 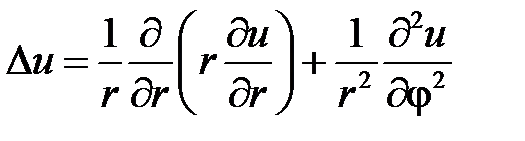 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах 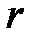 ,
, 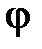 (
(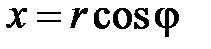 ,
, 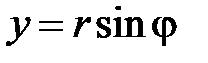 ). Граничное условие преобразуем в полярные координаты:
). Граничное условие преобразуем в полярные координаты:
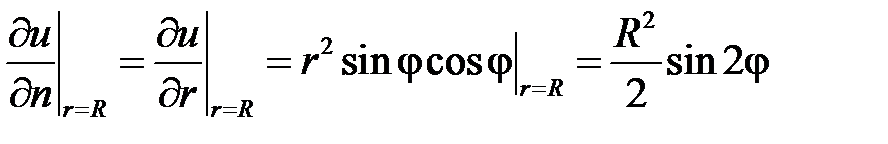 .
.
Из условия однозначности решения вытекает условие периодичности
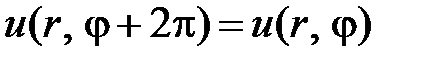 .
.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные решения уравнения 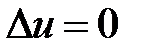 будем искать в виде
будем искать в виде
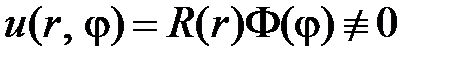 ,
,
Подставляем 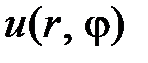 в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
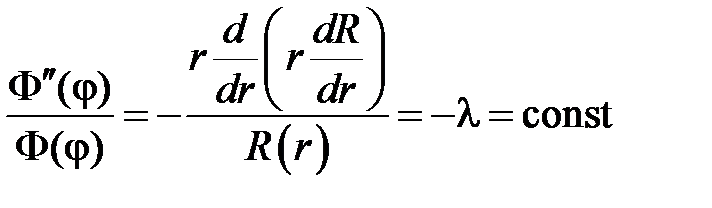 ,
,
откуда
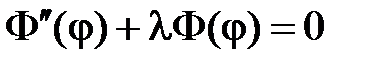 ,
,
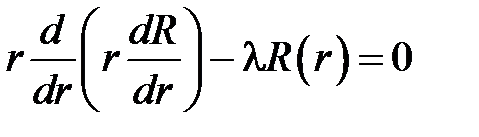 .
.
Из условия периодичности следует, что
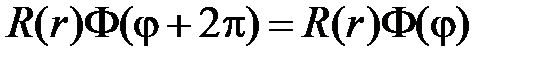 ,
, 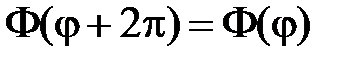 .
.
Таким образом, для 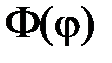 получаем задачу на собственные значения
получаем задачу на собственные значения
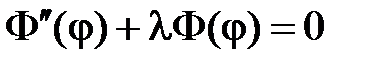 ,
,
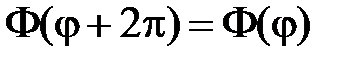 .
.
Если 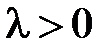 , то
, то
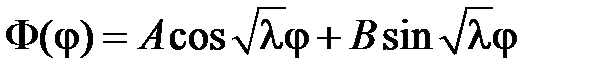 .
.
Применяем условие периодичности:
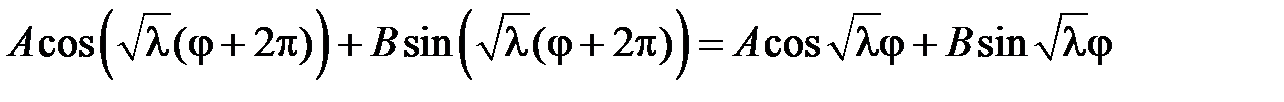 .
.
Отсюда, 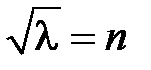 ,
, 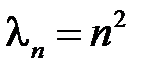 ,
, 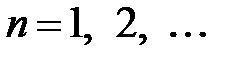 .
.
Если 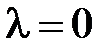 , то
, то
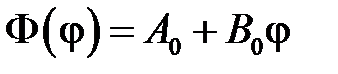 .
.
Следует взять 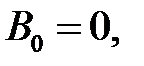 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При 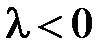 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
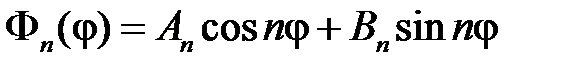 ,
, 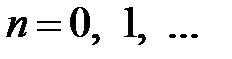 .
.
Чтобы решить уравнение для 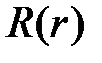 при
при 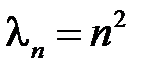 , сделаем замену
, сделаем замену 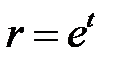 . Получим
. Получим
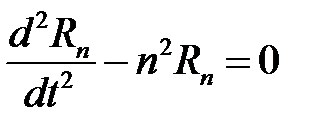 ,
, 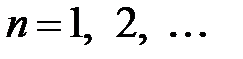 ,
,
откуда
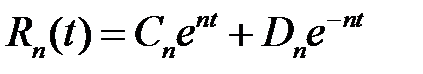 ,
,
т.е.
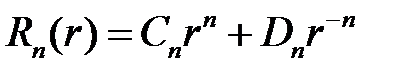 ,
, 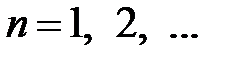 .
.
При 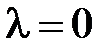 получим
получим 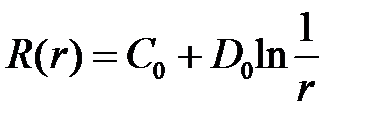 .
.
Таким образом, функции
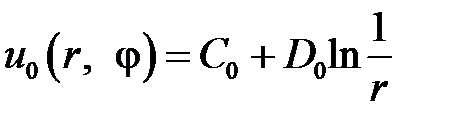 ,
,
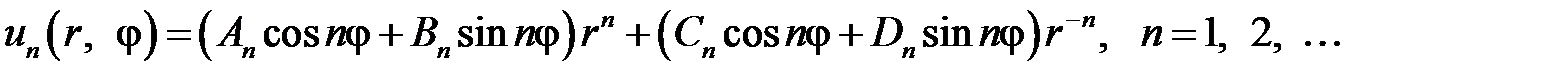
являются частными решениями уравнения 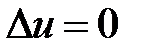 . Составим функцию
. Составим функцию
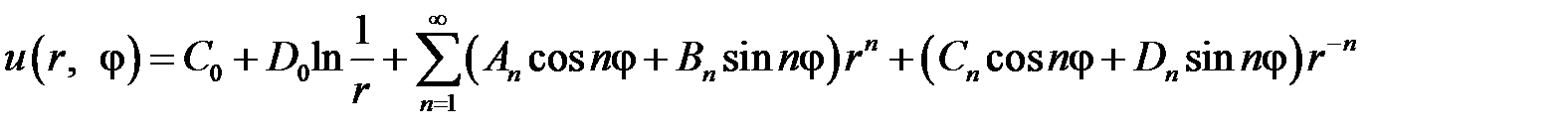 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Поскольку задача рассматривается во внешности круга радиуса 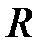 , то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными в области
, то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными в области 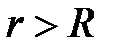 , т.е.
, т.е.
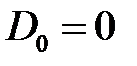 ,
, 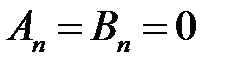 ,
, 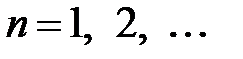 .
.
Итак, в области 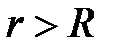 имеем
имеем
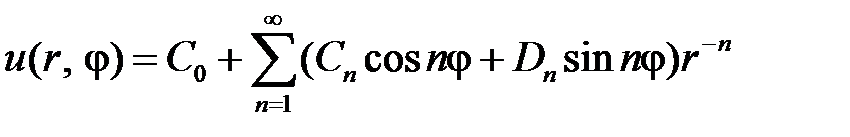 .
.
Для нахождения 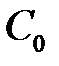 ,
, 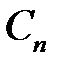 ,
, 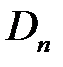 ,
, 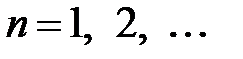 , воспользуемся граничным условием.
, воспользуемся граничным условием.
Находим
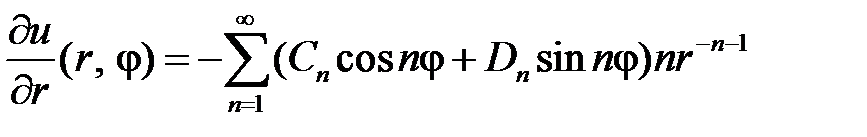 .
.
Тогда условие 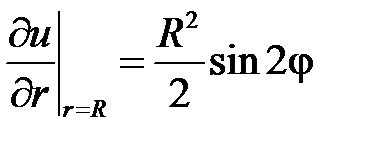 даёт:
даёт:
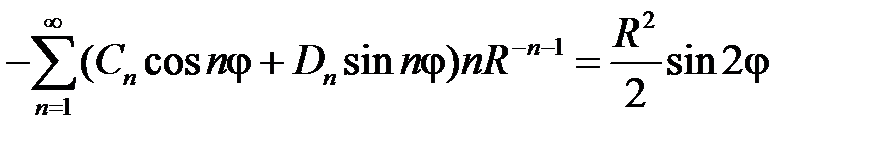 ,
,
откуда
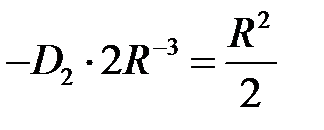 ,
, 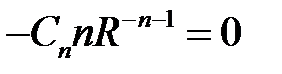 ,
, 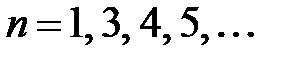
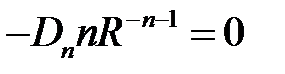 ,
, 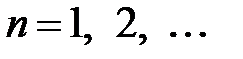 .
.
Тогда в ряде для 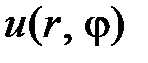 ненулевыми являются только коэффициенты
ненулевыми являются только коэффициенты
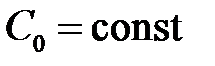 ,
, 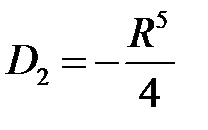 .
.
У нас 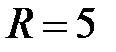 , поэтому окончательно решение заданной внешней задачи Неймана для уравнения Лапласа вне круга имеет вид
, поэтому окончательно решение заданной внешней задачи Неймана для уравнения Лапласа вне круга имеет вид
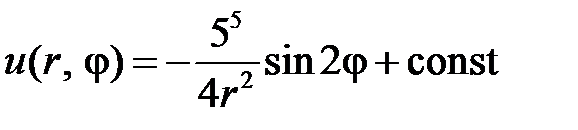 .
.
4. Воспользуемся формулой полной вероятности. Событие
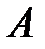 – взятая наудачу деталь из наудачу взятого набора является стандартной.
– взятая наудачу деталь из наудачу взятого набора является стандартной.
Введем гипотезы:
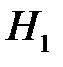 – для извлечения детали был выбран первый набор;
– для извлечения детали был выбран первый набор;
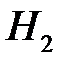 – для извлечения детали был выбран второй набор.
– для извлечения детали был выбран второй набор.
Считая выбор любого набора равновероятным, вероятности гипотез
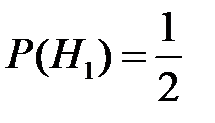 ,
, 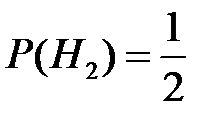 .
.
Условные вероятности 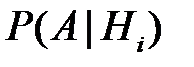 ,
, 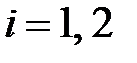 , по условию задачи равны
, по условию задачи равны
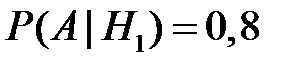 ,
, 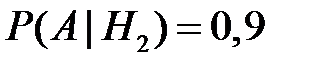 .
.
Тогда по формуле полной вероятности
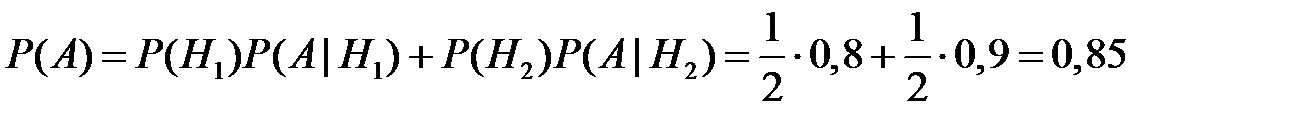 .
.
 2015-07-14
2015-07-14 421
421








