1. Уравнение Лапласа. Внутренняя задача Дирихле для уравнения Лапласа в круге.
2. Неравенство Чебышёва (с доказательством).
3. Найти потенциал в центре квадрата со стороной 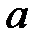 , если на трёх сторонах квадрата потенциал равен нулю, а на четвертой стороне задается формулой
, если на трёх сторонах квадрата потенциал равен нулю, а на четвертой стороне задается формулой
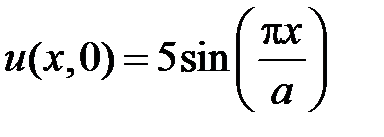 .
.
4. Найти функцию распределения случайной величины 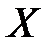 , заданной плотностью вероятности
, заданной плотностью вероятности 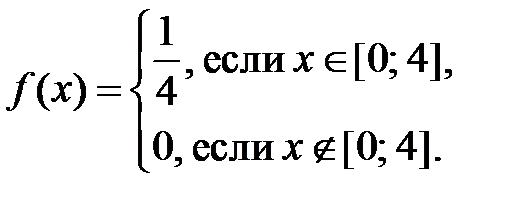 .
.
1. Уравнением Лапласа называется уравнение вида
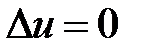 ,
,
где 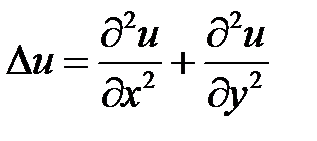 – оператор Лапласа.
– оператор Лапласа.
Внутренняя задача Дирихле для уравнения Лапласа в круга радиуса 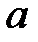 ставится следующим образом:
ставится следующим образом:
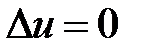 при
при  ,
,
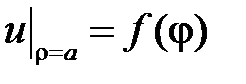 ,
,
где 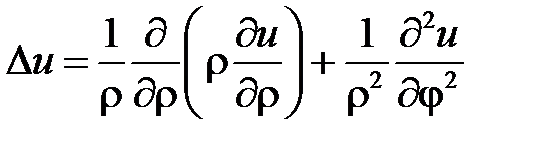 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах  ,
,  (
(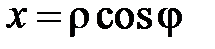 ,
, 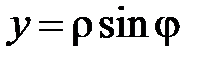 ),
), 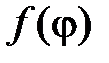 – заданная функция.
– заданная функция.
Из условия однозначности решения вытекает условие периодичности
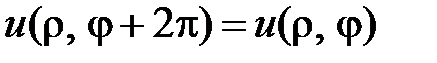 .
.
Кроме того, нужно поставить условие ограниченности решения в центре круга.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные решения уравнения 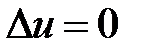 будем искать в виде
будем искать в виде
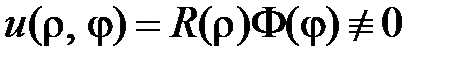 ,
,
Подставляем 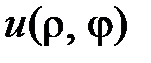 в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
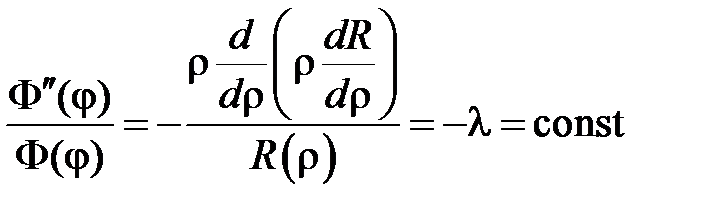 ,
,
откуда
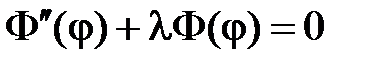 ,
,
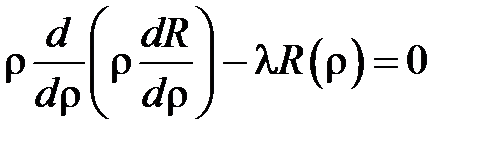 .
.
Из условия периодичности следует, что
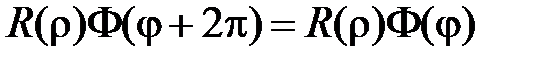 ,
, 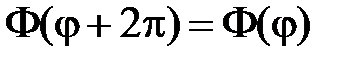 .
.
Таким образом, для 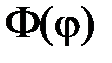 получаем задачу на собственные значения
получаем задачу на собственные значения
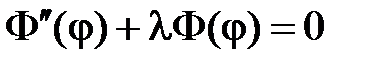 ,
,
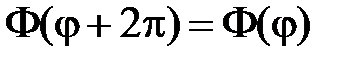 .
.
Если 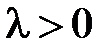 , то
, то
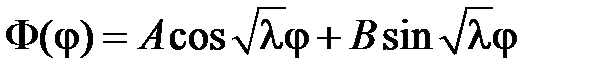 .
.
Применяем условие периодичности:
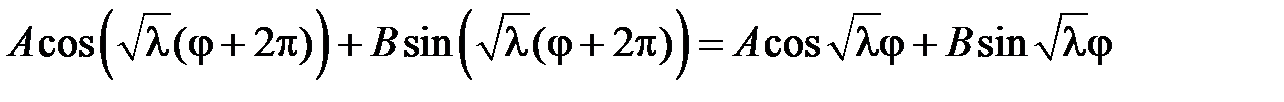 .
.
Отсюда, 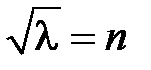 ,
, 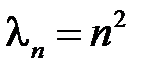 ,
, 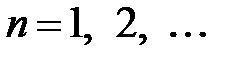 .
.
Если 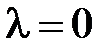 , то
, то
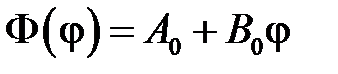 .
.
Следует взять 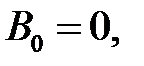 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При 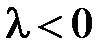 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
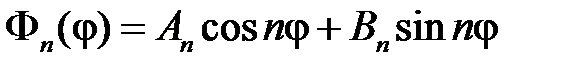 ,
, 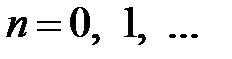 .
.
Чтобы решить уравнение для  при
при 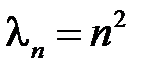 , сделаем замену
, сделаем замену 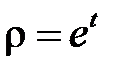 . Получим
. Получим
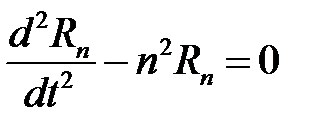 ,
, 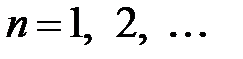 ,
,
откуда
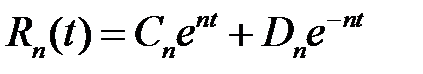 ,
,
т.е.
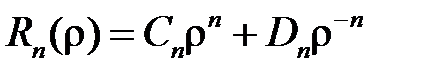 ,
, 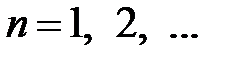 .
.
При 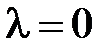 получим
получим 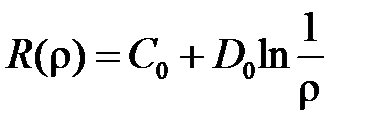 .
.
Таким образом, функции
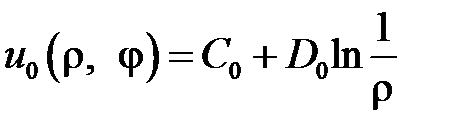 ,
,
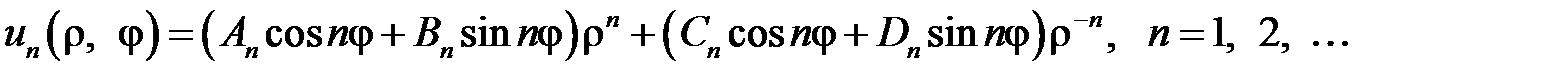
являются частными решениями уравнения 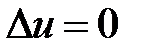 . Составим функцию
. Составим функцию
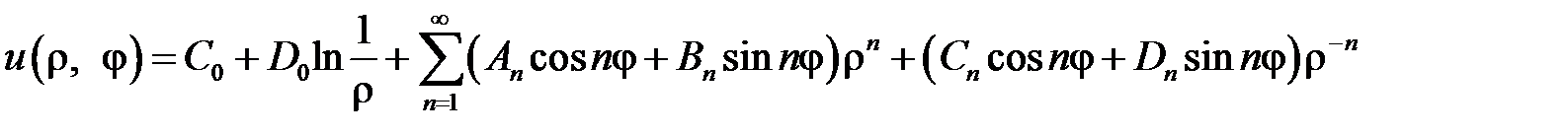 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Поскольку задача рассматривается внутри круга радиуса  , то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными при
, то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными при  , т.е.
, т.е.
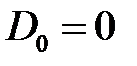 ,
, 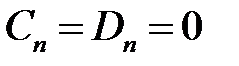 ,
, 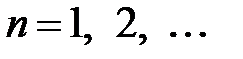 .
.
Итак, в области  имеем
имеем
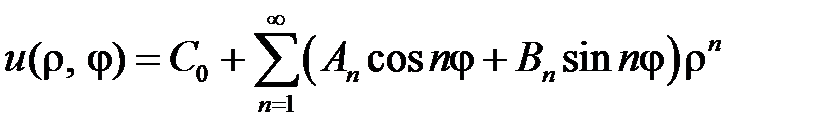 .
.
Для нахождения 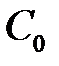 ,
, 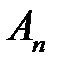 ,
, 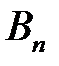 ,
,  , воспользуемся краевым условием
, воспользуемся краевым условием 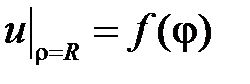 . Разложим функцию
. Разложим функцию 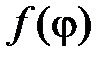 в тригонометрический ряд Фурье в промежутке
в тригонометрический ряд Фурье в промежутке 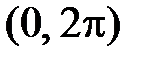 :
:
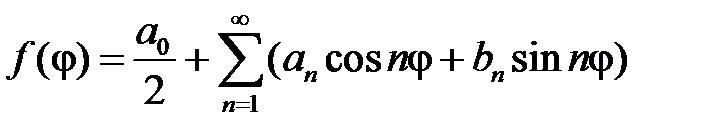 ,
,
где 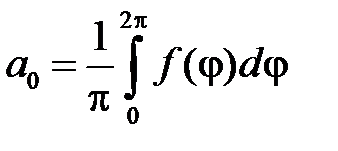 ,
, 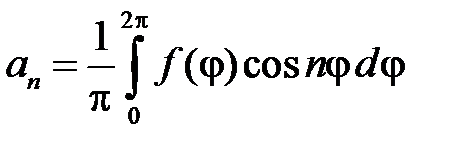 ,
, 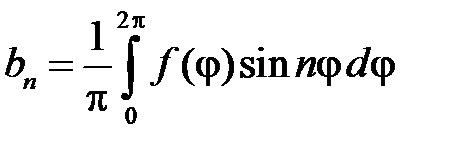 ,
, 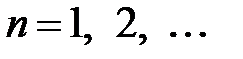 .
.
Тогда краевое условие 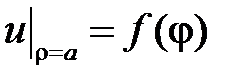 дает равенство
дает равенство
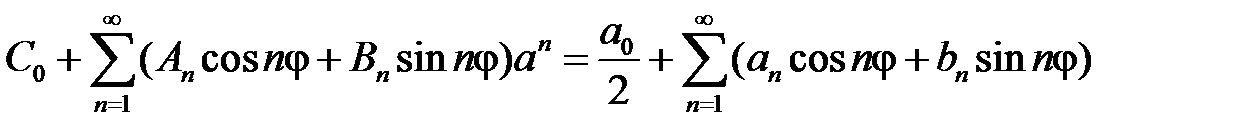 ,
,
откуда
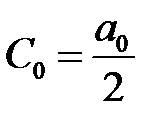 ,
, 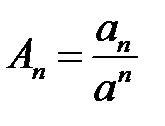 ,
, 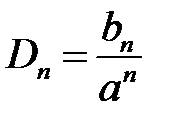 ,
, 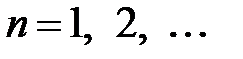 .
.
Окончательно решение внешней задачи Дирихле для уравнения Лапласа в круге имеет вид
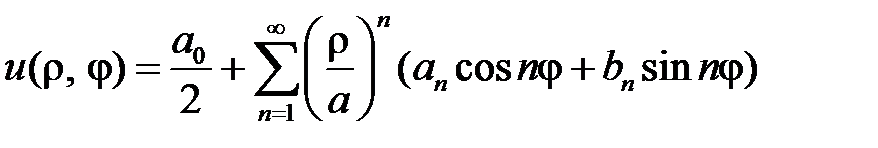 .
.
2. Для любой случайной величины 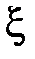 и любого положительного числа
и любого положительного числа 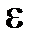 справедливо неравенство Чебышева
справедливо неравенство Чебышева
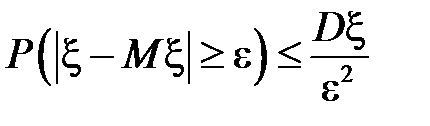 .
.
Доказательство проведем для случая, когда 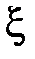 – непрерывная случайная величина. Пусть
– непрерывная случайная величина. Пусть 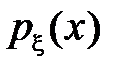 – плотность случайной величины
– плотность случайной величины 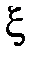 , а
, а 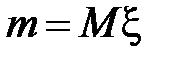 , тогда
, тогда
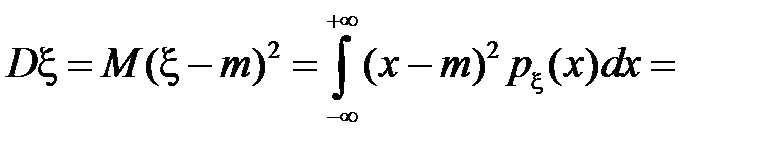
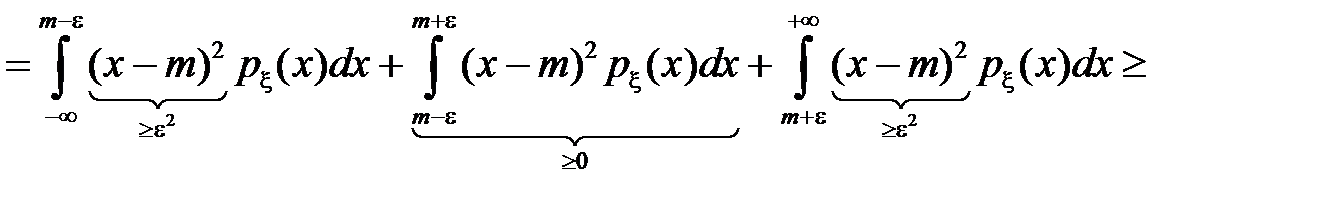
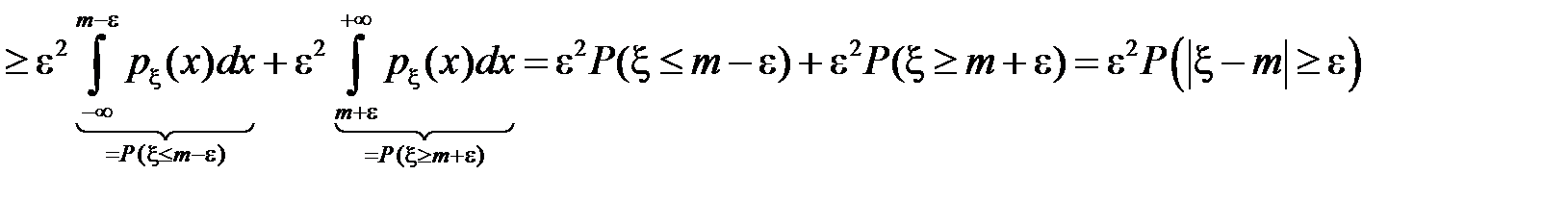 ,
,
так как события 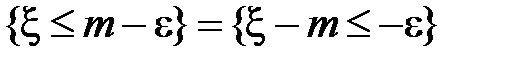 и
и 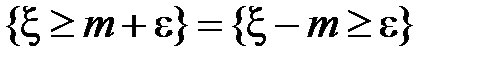 несовместны.
несовместны.
Итак,
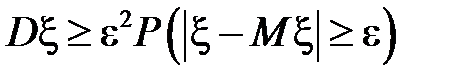 ,
,
то есть
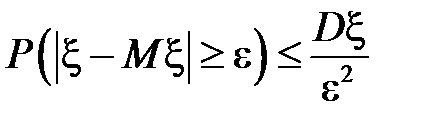 .
.
Неравенство Чебышева доказано.
Для дискретных случайных величин неравенство Чебышева доказывается аналогично (вместо интегралов будут суммы рядов).
Следствие. Поскольку 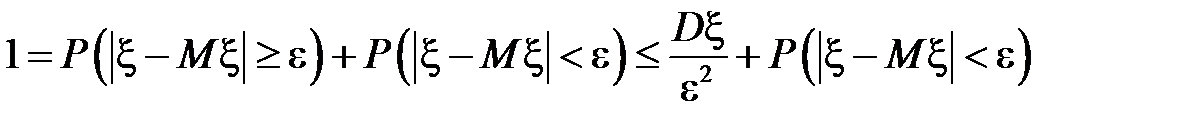 , то
, то
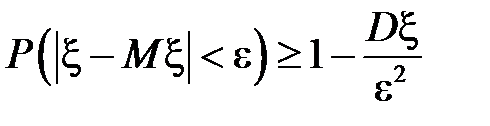 .
.
3. Если 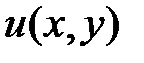 – искомый потенциал, то он является решением задачи
– искомый потенциал, то он является решением задачи
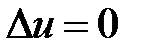 при
при 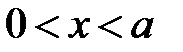 ,
, 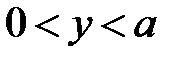 ,
,
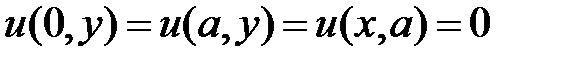 ,
, 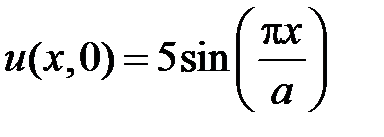 .
.
Для решения краевой задачи воспользуемся методом Фурье. Нетривиальные решения уравнения Лапласа 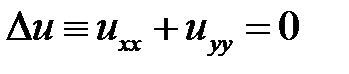 будем искать в виде
будем искать в виде 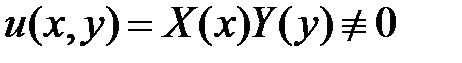 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
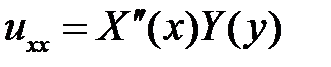 ,
, 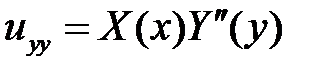 ,
,
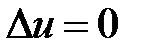 :
: 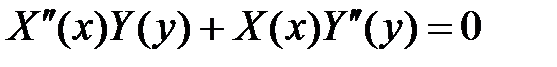 ,
,
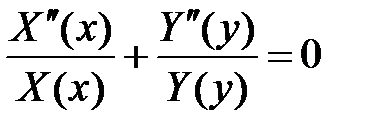 ,
, 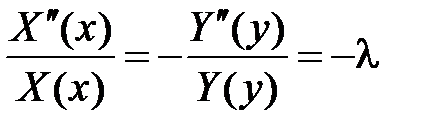 ,
, 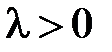 .
.
Тогда функции 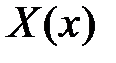 и
и 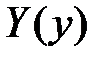 являются соответственно решениями уравнений
являются соответственно решениями уравнений
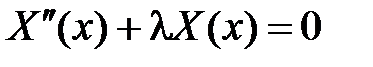 ,
, 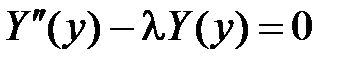 .
.
Из краевых условий 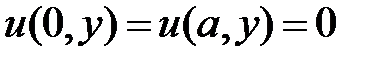 получаем краевые условия для функции
получаем краевые условия для функции 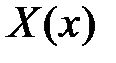 :
: 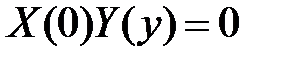 ,
, 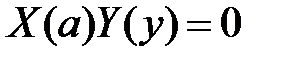 , значит,
, значит, 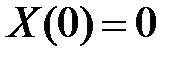 ,
, 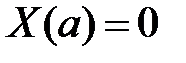 . Таким образом, для определения
. Таким образом, для определения 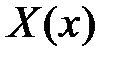 и
и 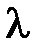 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
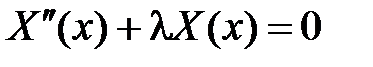
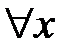 :
: 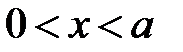 ,
,
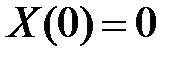 ,
, 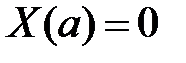 .
.
Поскольку 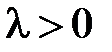 , то общее решение уравнения
, то общее решение уравнения 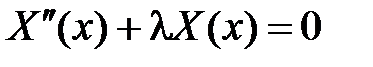 имеет вид
имеет вид
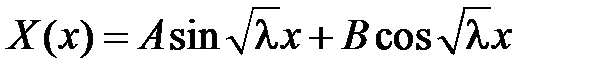 .
.
Из краевого условия 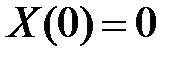 получаем:
получаем: 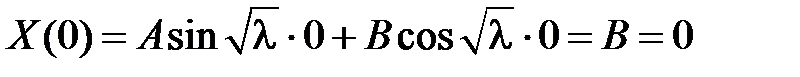 , т.е.
, т.е. 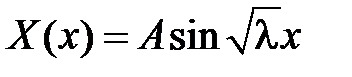 . Из краевого условия
. Из краевого условия 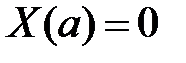 получаем:
получаем: 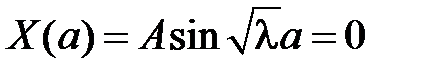 . Поскольку
. Поскольку 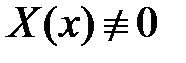 , то
, то 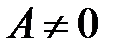 и равенство
и равенство 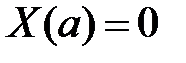 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 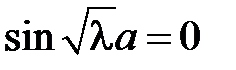 , откуда получаем
, откуда получаем 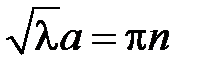 ,
, 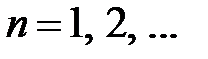 , т.е.
, т.е. 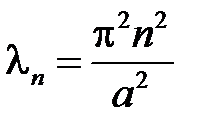 ,
, 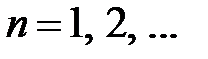 . Тогда получим
. Тогда получим 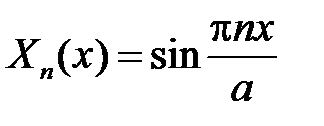 ,
, 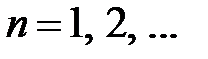 . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
Собственные функции 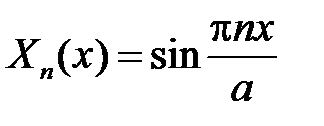 ,
, 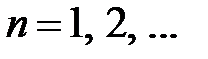 .
.
Теперь при каждом 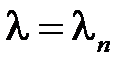 решаем уравнение для
решаем уравнение для 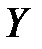 :
:
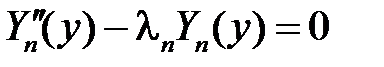
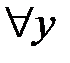 :
: 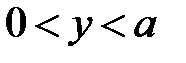 ,
, 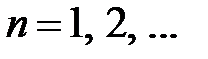 .
.
Общее решение этого уравнения имеет вид
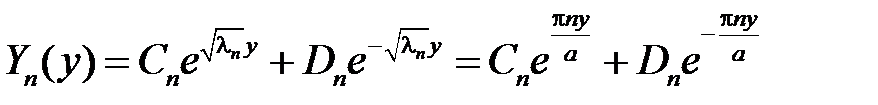 .
.
Тогда
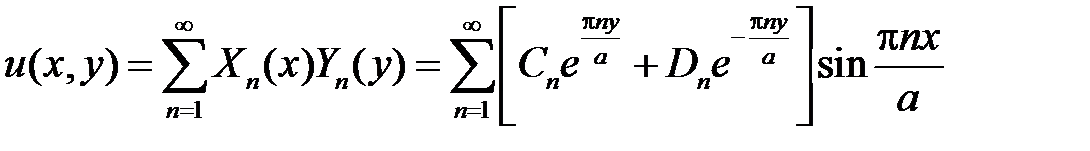 .
.
Краевые условия 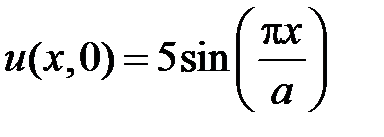 ,
, 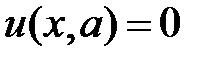 дают:
дают:
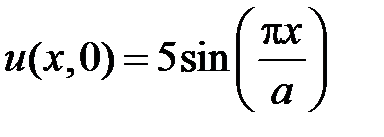 :
: 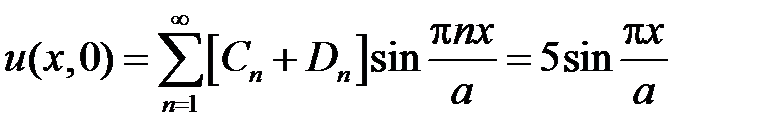
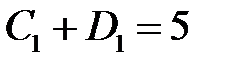 ;
; 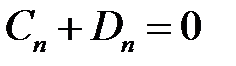 ,
, 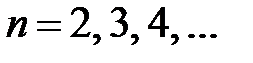 ;
;
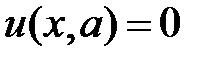 :
:
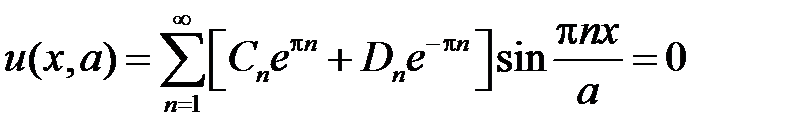
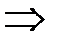
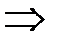
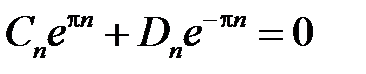 ,
, 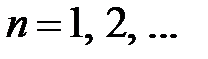 .
.
Итак, для определения 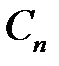 ,
, 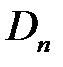 ,
, 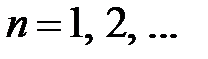 , получили системы
, получили системы
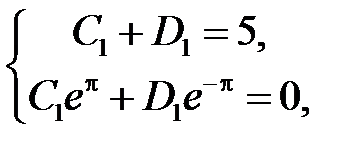
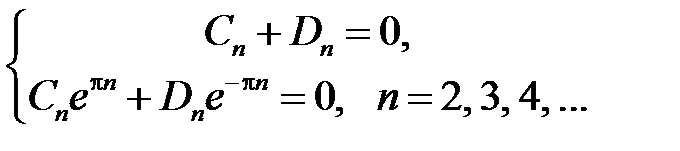
Решая их, получим
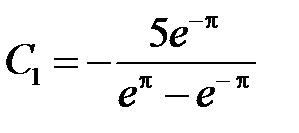 ,
, 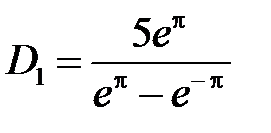 ,
,
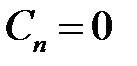 ,
, 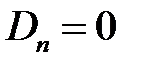 ,
, 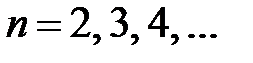 .
.
Тогда
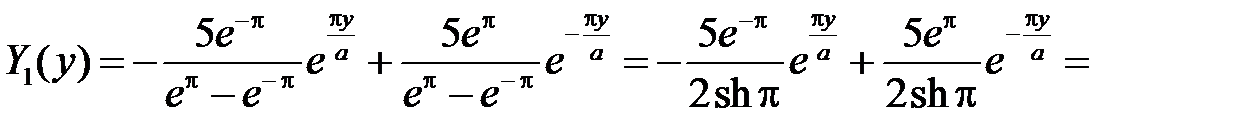
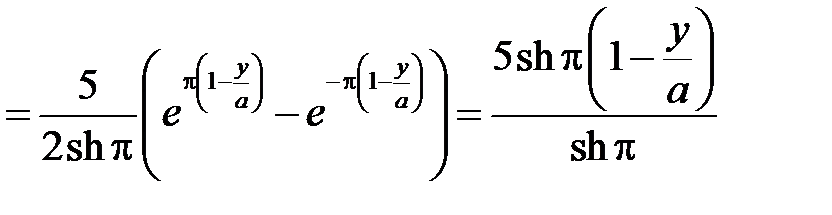 ,
,
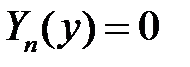 ,
, 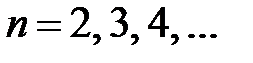 .
.
Окончательно, потенциал равен
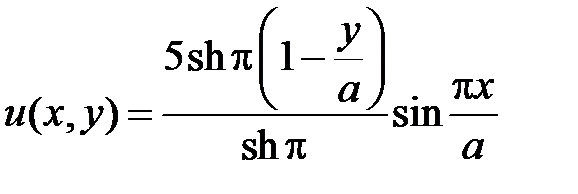 .
.
Значение потенциала в центре квадрата со стороной 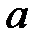 , т.е. в точке
, т.е. в точке 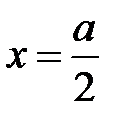 ,
, 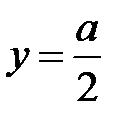 , равно
, равно
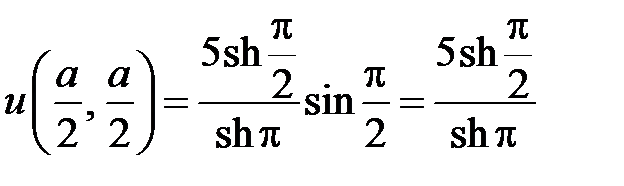 .
.
4. Функцию распределения найдем по формуле
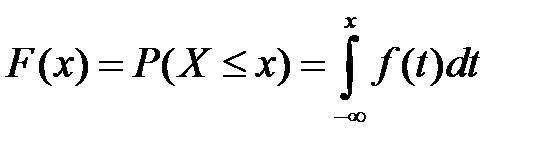 .
.
Для заданной плотности получим:
при 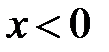
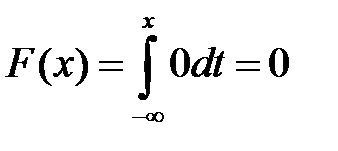 ;
;
при 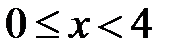
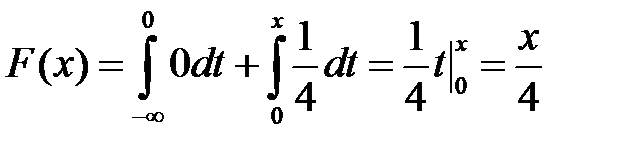 ,
,
при 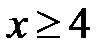
 .
.
Итак, функция распределения равна
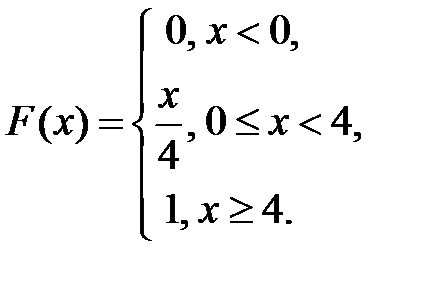
 2015-07-14
2015-07-14 994
994








