1. Задача Дирихле для уравнения Лапласа в прямоугольнике.
2. Теорема сложения вероятностей (с доказательством). Вероятность противоположного события.
3. Решить задачу Дирихле для уравнения Лапласа 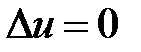 вне круга радиуса
вне круга радиуса 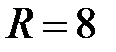 . ГУ:
. ГУ: 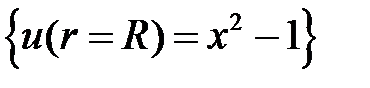 .
.
4. Найти закон распределения числа попаданий в мишень при четырёх выстрелах, если вероятность попадания при каждом выстреле равна 0,8.
1. Задача Дирихле для уравнения Лапласа в прямоугольнике имеет вид
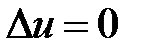
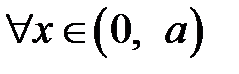 ,
, 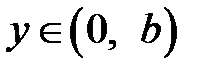 ,
,
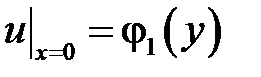 ,
, 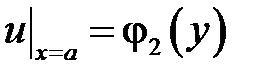 ,
,
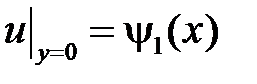 ,
, 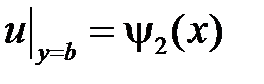 .
.
Эту задачу разобьем на две задачи, каждая из которых имеет однородные граничные условия по одной из переменных. Пусть
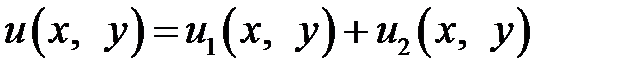 ,
,
где 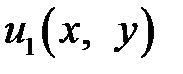 и
и 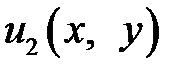 являются соответственно решениями таких задач в прямоугольнике:
являются соответственно решениями таких задач в прямоугольнике:
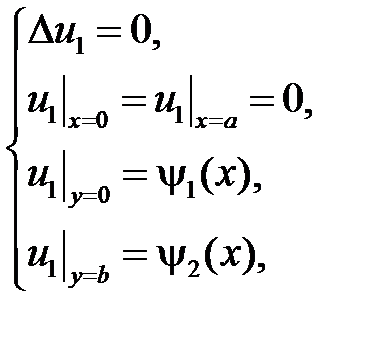
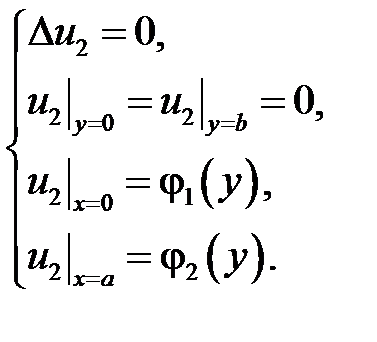
Рассмотрим сначала задачу для 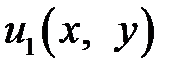 . Согласно методу Фурье будем искать решения в виде
. Согласно методу Фурье будем искать решения в виде
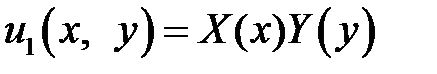 .
.
Подставляем в уравнение и разделяем переменные:
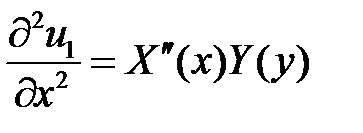 ,
, 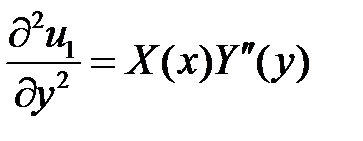 ,
,
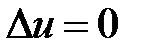 :
: 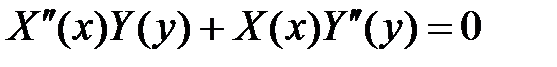 ,
,
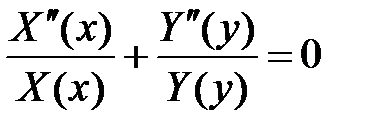 ,
, 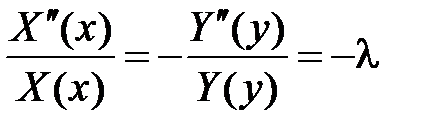 ,
, 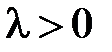 .
.
Тогда функции 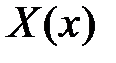 и
и 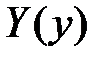 являются соответственно решениями уравнений
являются соответственно решениями уравнений
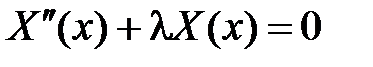 ,
, 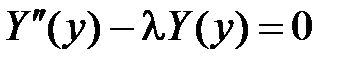 .
.
Из краевых условий 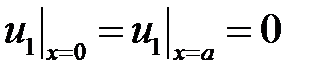 получаем краевые условия для функции
получаем краевые условия для функции 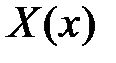 :
: 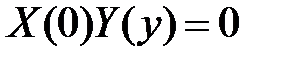 ,
, 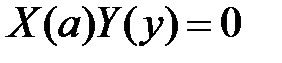 , значит,
, значит, 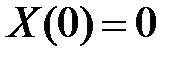 ,
, 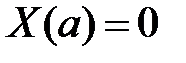 . Таким образом, для определения
. Таким образом, для определения 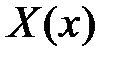 и
и 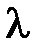 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
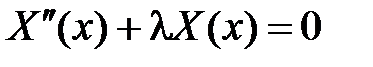
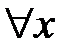 :
: 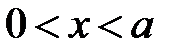 ,
,
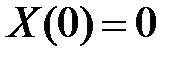 ,
, 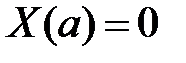 .
.
Поскольку 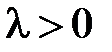 , то общее решение уравнения
, то общее решение уравнения 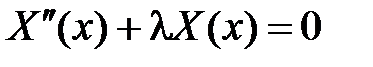 имеет вид
имеет вид
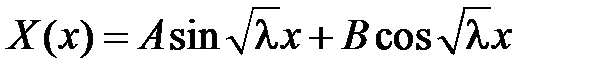 .
.
Из краевого условия 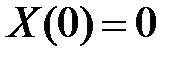 получаем:
получаем: 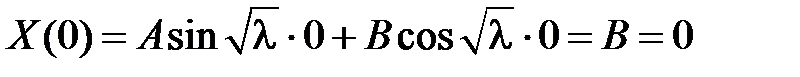 , т.е.
, т.е. 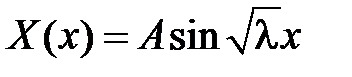 . Тогда из краевого условия
. Тогда из краевого условия 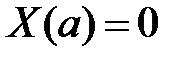 получаем:
получаем: 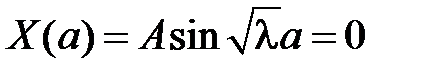 . Поскольку
. Поскольку 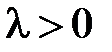 и
и 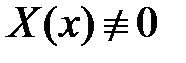 , то
, то 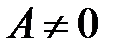 и равенство
и равенство 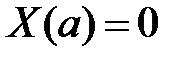 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 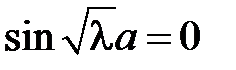 , откуда получаем
, откуда получаем 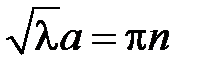 ,
, 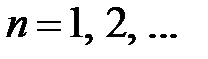 , т.е.
, т.е. 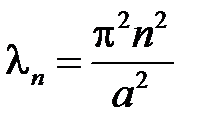 ,
, 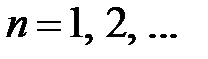 . Тогда получим
. Тогда получим 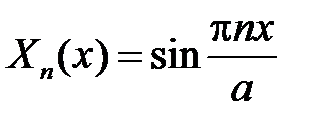 ,
, 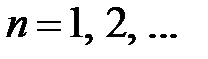 . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные функции 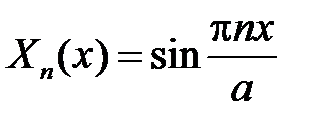 ,
, 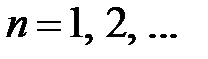 .
.
Теперь при каждом 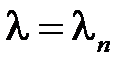 решаем уравнение для
решаем уравнение для 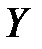 :
:
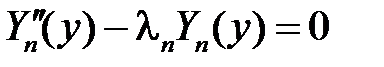
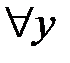 :
: 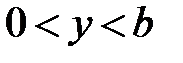 ,
, 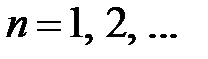 .
.
Общее решение этого уравнения имеет вид
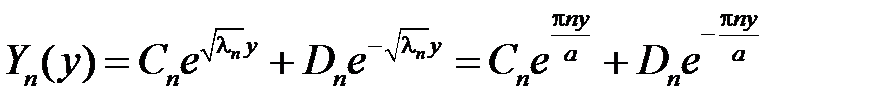 .
.
Тогда
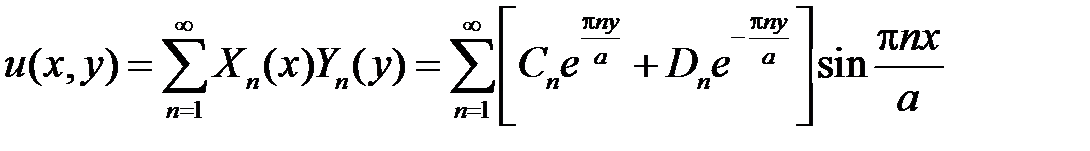 .
.
Граничные условия 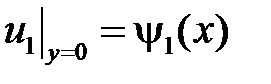 и
и 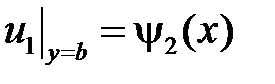 приводят к равенствам:
приводят к равенствам:
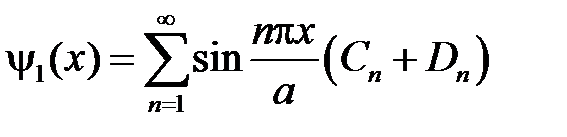 ,
, 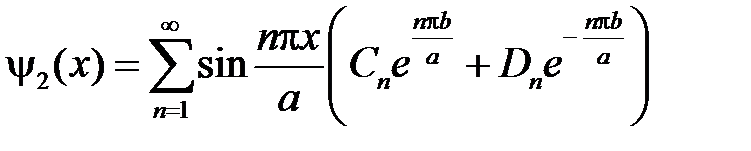 .
.
Пусть
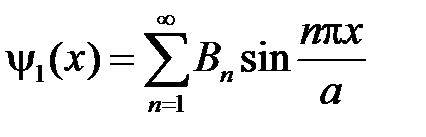 и
и 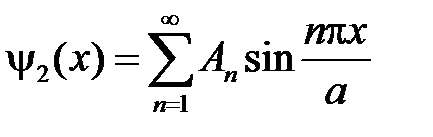 ,
,
где
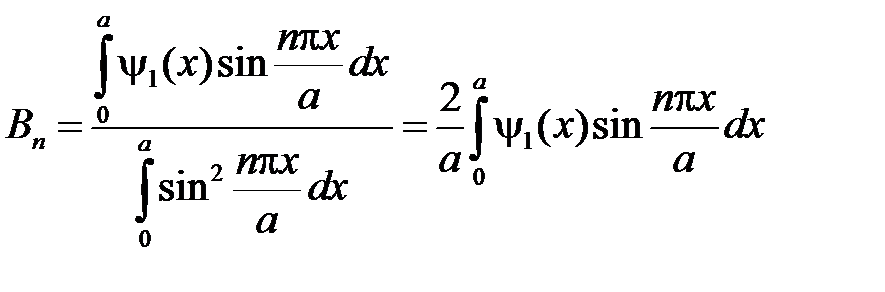 ,
,
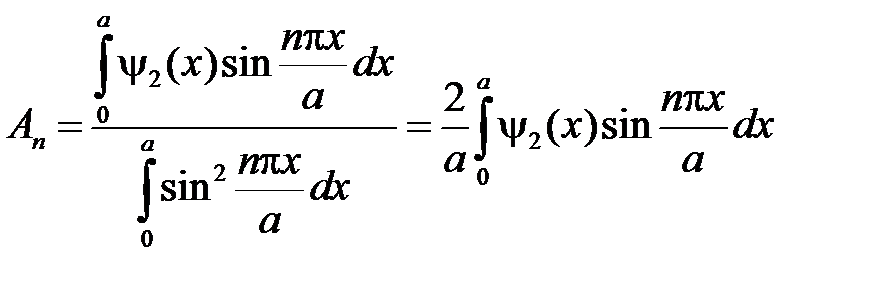
– соответствующие ряды Фурье функций 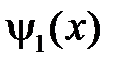 и
и 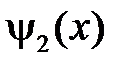 по системе функций
по системе функций 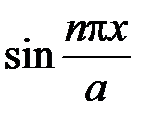 ,
,  . Тогда
. Тогда
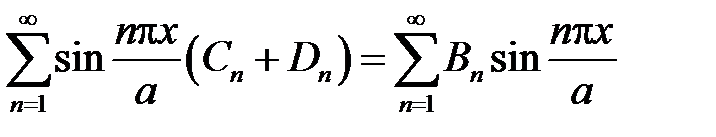 ,
,
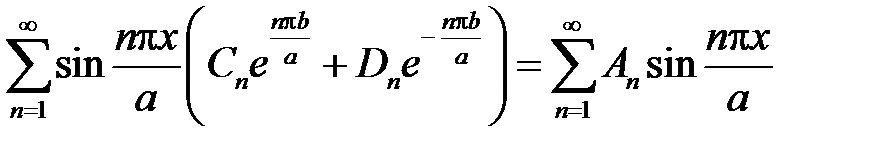 ,
,
откуда
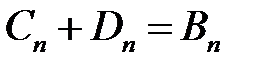 ,
, 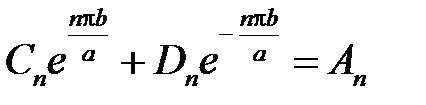 ,
,  ,
,
и
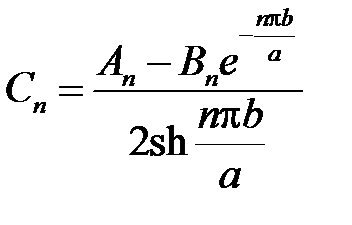 ,
, 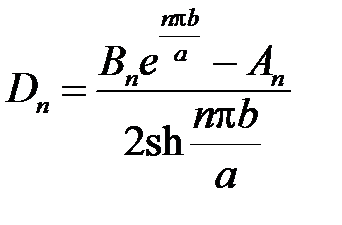 ,
, 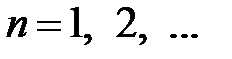 .
.
Тогда
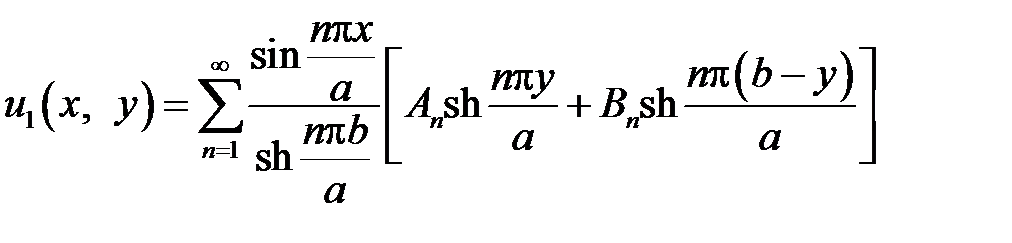 .
.
Аналогично решается задача для 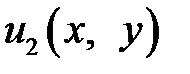 :
:
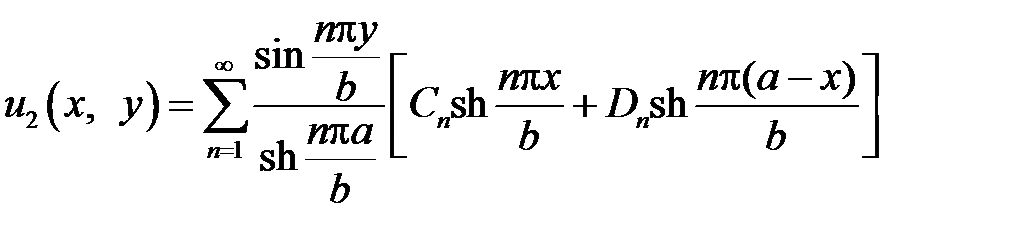 ,
,
где
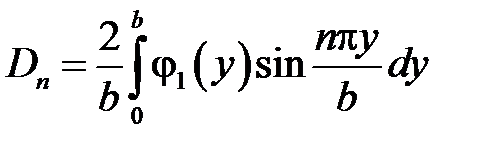 ,
, 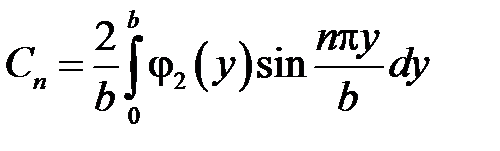 .
.
Значит, решение задачи Дирихле для уравнения Лапласа в прямоугольнике
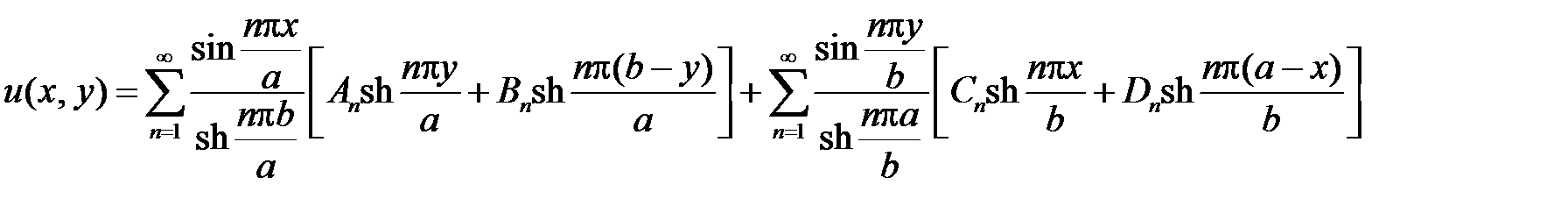 .
.
2. Теорема сложения вероятностей. Если события 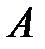 и
и 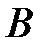 совместны, то
совместны, то
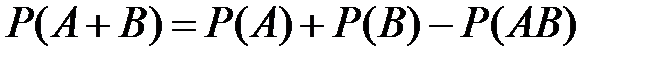 .
.
Доказательство. Пусть 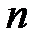 – числе всех равновозможных исходов испытания, в результате которого могут появиться события
– числе всех равновозможных исходов испытания, в результате которого могут появиться события 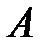 и
и 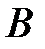 . Пусть
. Пусть 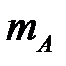 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 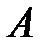 ,
, 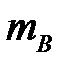 – число тех исходов, которые благоприятствуют событию
– число тех исходов, которые благоприятствуют событию 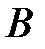 ,
, 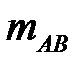 – число тех исходов, которые благоприятствуют произведению событий
– число тех исходов, которые благоприятствуют произведению событий 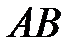 . Тогда событию
. Тогда событию 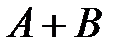 благоприятствуют исходы числом
благоприятствуют исходы числом 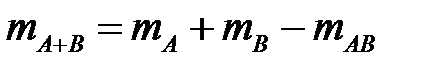 . Значит, по формуле классической вероятности
. Значит, по формуле классической вероятности
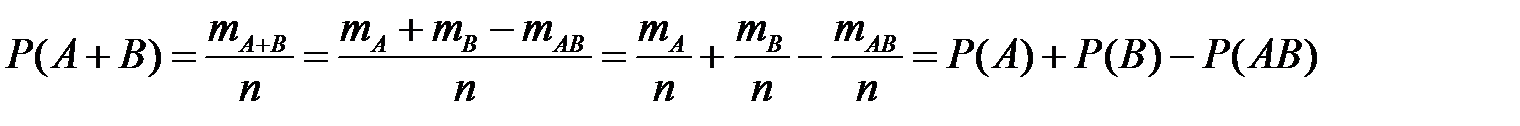 .
.
Следствие. Если события 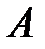 и
и 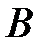 несовместны, то
несовместны, то 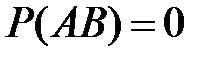 и
и
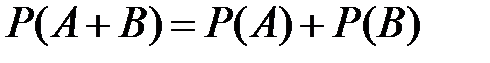 .
.
Для трех событий 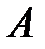 ,
, 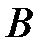 и
и  теорема сложения имеет вид
теорема сложения имеет вид
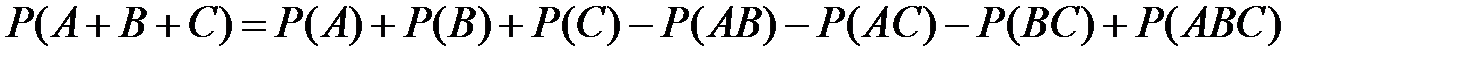 .
.
Для 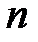 событий теорема сложения имеет вид
событий теорема сложения имеет вид
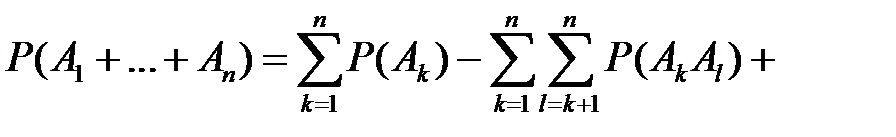
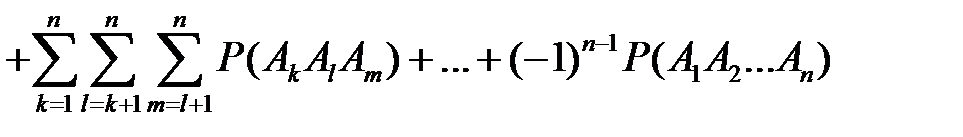 .
.
Противоположные события 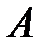 и
и 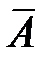 несовместны и в сумме дают достоверное событие, поэтому
несовместны и в сумме дают достоверное событие, поэтому
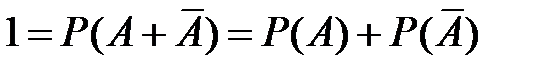 ,
,
откуда получаем формулу для вероятности противоположного события
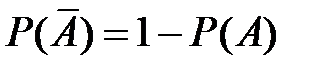 .
.
3. Внешняя задача Дирихле для уравнения Лапласа вне круга радиуса 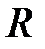 ставится следующим образом:
ставится следующим образом:
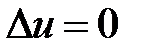 при
при 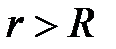 ,
,
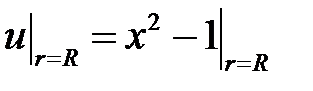 ,
,
где 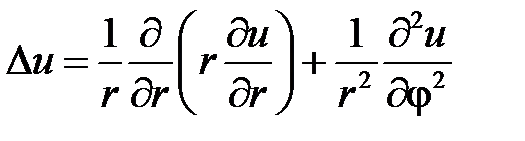 – оператор Лапласа в полярных координатах
– оператор Лапласа в полярных координатах 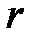 ,
,  (
(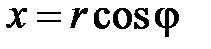 ,
, 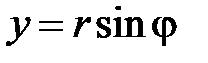 ). Граничное условие преобразуем в полярные координаты:
). Граничное условие преобразуем в полярные координаты:
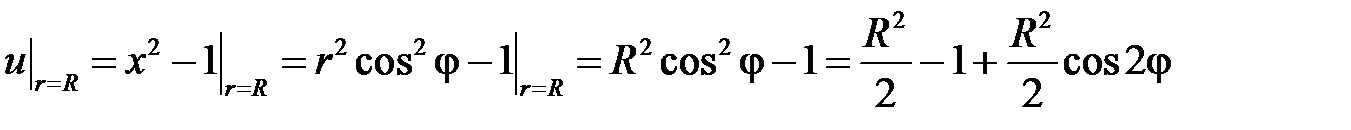 .
.
Из условия однозначности решения вытекает условие периодичности
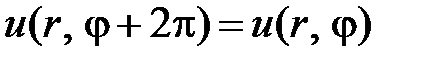 .
.
Для нахождения решения этой задачи используем метод Фурье.
Нетривиальные решения уравнения 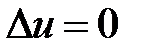 будем искать в виде
будем искать в виде
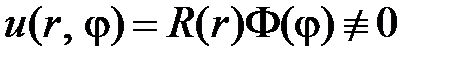 ,
,
Подставляем  в уравнение и разделяем переменные:
в уравнение и разделяем переменные:
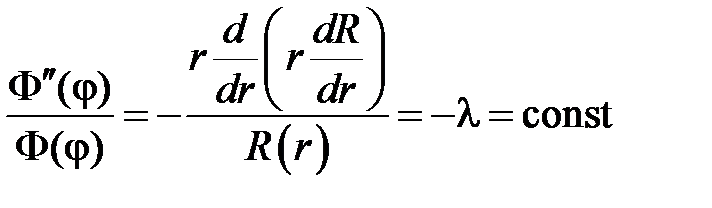 ,
,
откуда
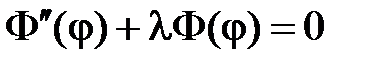 ,
,
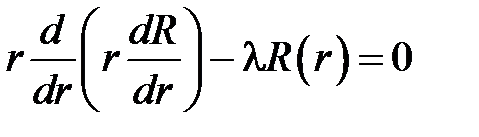 .
.
Из условия периодичности следует, что
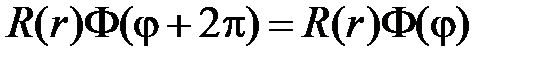 ,
, 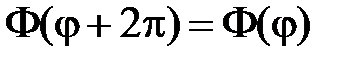 .
.
Таким образом, для 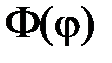 получаем задачу на собственные значения
получаем задачу на собственные значения
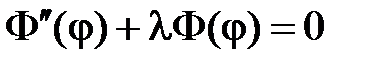 ,
,
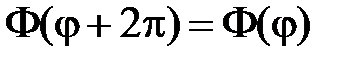 .
.
Если 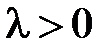 , то
, то
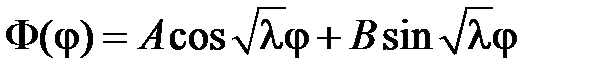 .
.
Применяем условие периодичности:
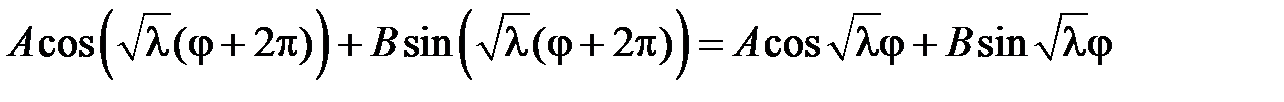 .
.
Отсюда, 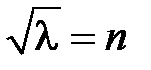 ,
, 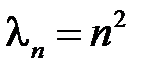 ,
, 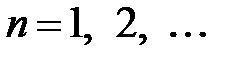 .
.
Если 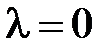 , то
, то
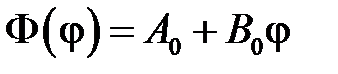 .
.
Следует взять 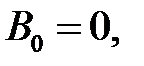 иначе не выполнится условие периодичности.
иначе не выполнится условие периодичности.
При 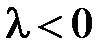 ненулевых периодических решений нет.
ненулевых периодических решений нет.
Окончательно имеем
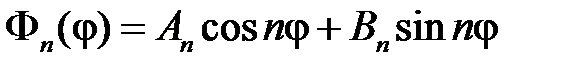 ,
, 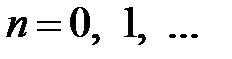 .
.
Чтобы решить уравнение для 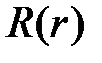 при
при 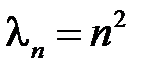 , сделаем замену
, сделаем замену 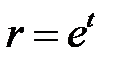 . Получим
. Получим
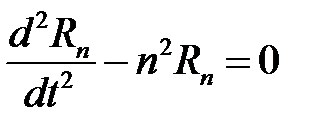 ,
, 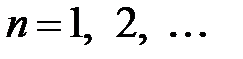 ,
,
откуда
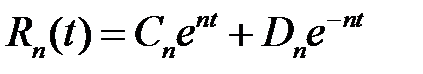 ,
,
т.е.
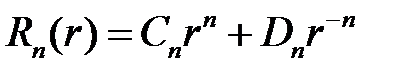 ,
, 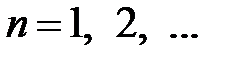 .
.
При 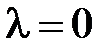 получим
получим 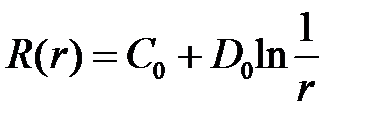 .
.
Таким образом, функции
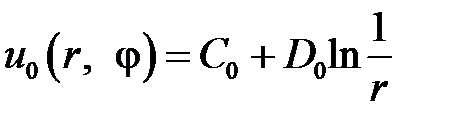 ,
,
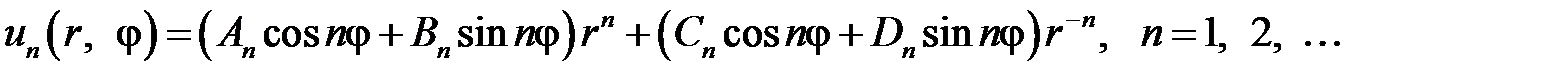
являются частными решениями уравнения 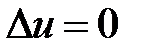 . Составим функцию
. Составим функцию
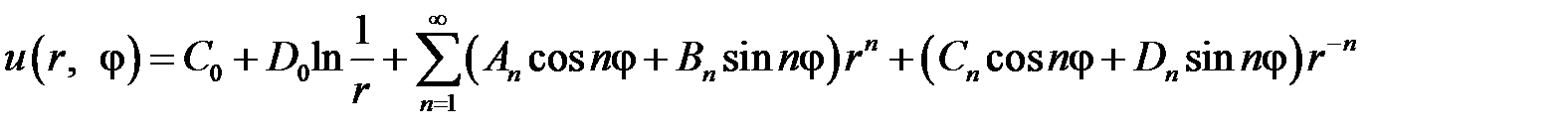 ,
,
которая вследствие линейности и однородности уравнения Лапласа также будет его решением.
Поскольку задача рассматривается во внешности круга радиуса 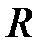 , то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными в области
, то следует положить равными нулю коэффициенты при частных решениях, которые является неограниченными в области 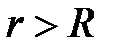 , т.е.
, т.е.
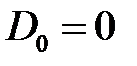 ,
, 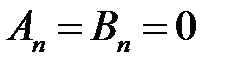 ,
, 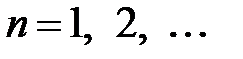 .
.
Итак, в области  имеем
имеем
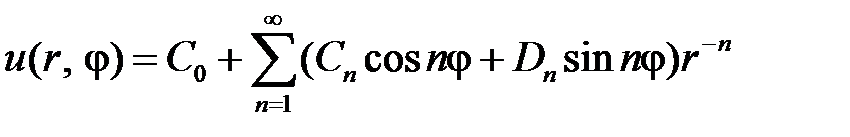 .
.
Для нахождения 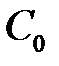 ,
, 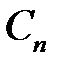 ,
, 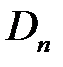 ,
, 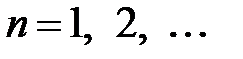 , воспользуемся граничным условием
, воспользуемся граничным условием 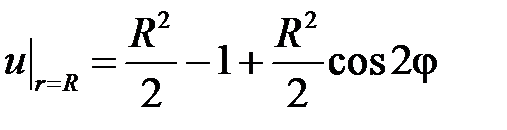 :
:
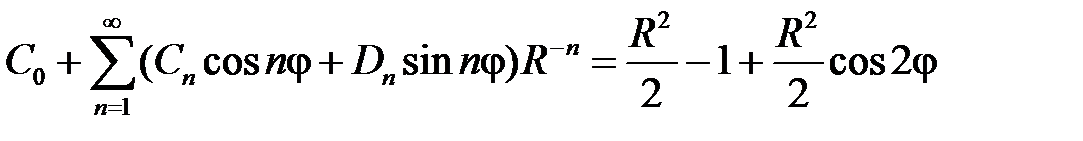 ,
,
откуда
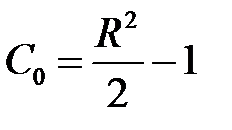 ,
, 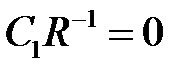 ,
, 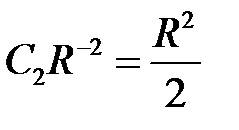 ,
, 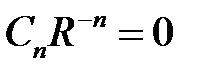 ,
, 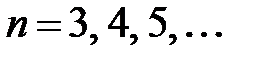
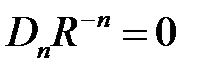 ,
, 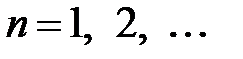 .
.
Тогда в ряде для 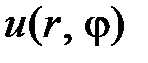 ненулевыми являются только коэффициенты
ненулевыми являются только коэффициенты
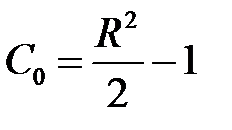 ,
, 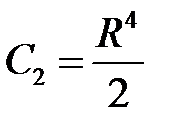 .
.
По условию 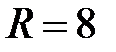 , поэтому
, поэтому
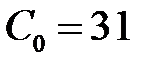 ,
, 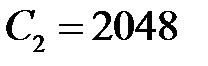 .
.
и окончательно решение заданной внешней задачи Дирихле для уравнения Лапласа вне круга имеет вид
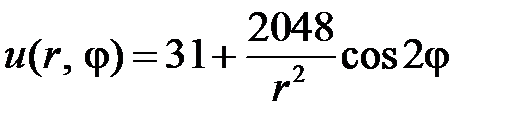 .
.
4. Здесь мы имеем дело с испытаниями по схеме Бернулли, где «успех» – попадание по мишени, вероятность «успеха» 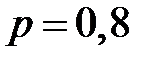 , всего
, всего 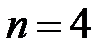 испытаний. Случайная величина
испытаний. Случайная величина 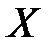 – число попаданий в мишень при четырёх выстрелах – имеет биномиальное распределение. Тогда
– число попаданий в мишень при четырёх выстрелах – имеет биномиальное распределение. Тогда 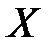 принимает значения
принимает значения 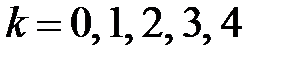 с вероятностями
с вероятностями
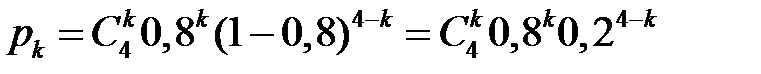
Находим:
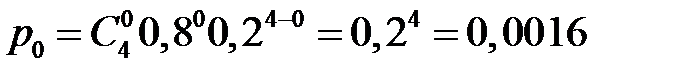 ,
,
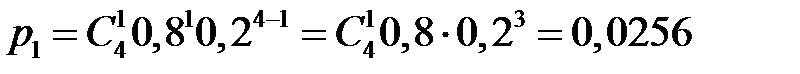 ,
,
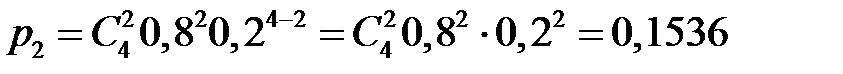 ,
,
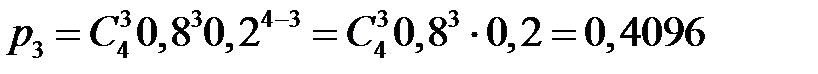 ,
,
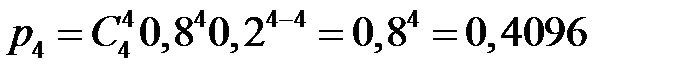
Итак, закон распределения числа попаданий в мишень при четырёх выстрелах имеет вид
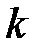 | |||||
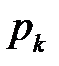 | 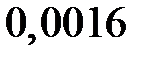 | 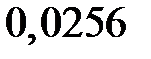 |  | 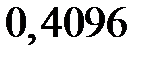 | 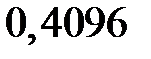 |
 2015-07-14
2015-07-14 1092
1092








