Напряжение постоянного тока и постоянный ток характеризуются величиной и полярностью.
Переменный ток и напряжение промышленной частоты имеют синусоидальную форму
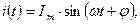
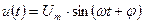 и характеризуются следующими значениями:
и характеризуются следующими значениями:
1. Мгновенным значением 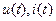 .
.
2. Максимальным (амплитудным, пиковым) значением 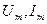 .
.
3. Постоянной составляющей 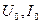 .
.
4. Средневыпрямленным значением 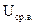 ,
, 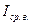 .
.
5. Среднеквадратическим (действующим, эффективным) значением 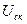 ,
,  .
.
Мгновенное значение тока (напряжения) – это значение сигнала в заданный момент времени Оно может наблюдаться на осциллографе и быть вычислено по осциллограмме для каждого момента времени.
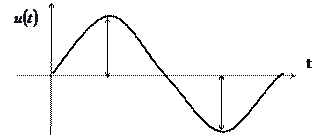
Максимальным значением напряжения (тока) называют наибольшее мгновенное значение напряжения на протяжении периода Т.
 |
Um+
0 Um-
Пиковое отклонение “вверх” и “вниз” – это соответственно наибольшее и наименьшее мгновенные значения переменной составляющей сигнала на протяжении заданного периода Т.
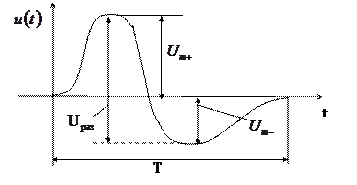
Разность между максимальным и минимальным значениями сигнала на протяжении заданного периода называется "размахом" напряжения 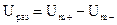
Постоянная составляющая (среднее значение) напряжения (тока) является среднеарифметическим мгновенных значений на протяжении периода Т.
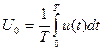 . (3)
. (3)
Величину постоянной составляющей сигнала за период можно найти и графически. Для этого необходимо из площади, находящейся над осью абсцисс 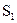 , вычесть площадь под осью абсцисс
, вычесть площадь под осью абсцисс 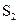 и полученную разность разделить на период. Иначе: ось времени надо переместить так, чтобы площади, занимаемые кривой напряжения над и под осью абсцисс, были равными.
и полученную разность разделить на период. Иначе: ось времени надо переместить так, чтобы площади, занимаемые кривой напряжения над и под осью абсцисс, были равными.
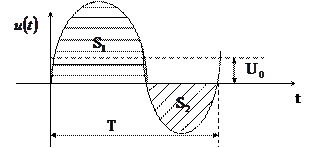 |
Отсюда следует, что у всех электрических сигналов, симметричных относительно оси абсцисс (например, синусоидальный сигнал), постоянная составляющая равна 0.
Пример 1. Определить постоянную составляющую сигнала (напряжения), приведенного на рисунке:
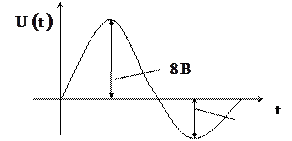 а) используем графический способ: размах амплиту-
а) используем графический способ: размах амплиту-
ды сигнала составит 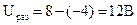 . Учитывая,
. Учитывая,
что для "синуса" размах 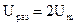 , получим
, получим 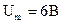 ,
,
Следовательно постоянная составляющая сигнала
равна 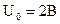 , а функция имеет вид:
, а функция имеет вид:
0 4В 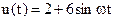 .
.
б) определим 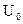 расчётным путём:
расчётным путём:
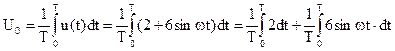 ,
,
т.к. интеграл от синуса любого угла за период равен нулю, получим
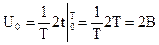 .
.
Средневыпрямленное значение – определяется как среднее арифметическое из модуля мгновенных значений
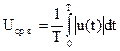 . (4)
. (4)
При однополярных напряжениях постоянная составляющая равна средневыпрямленному значению (см. ф-лы 3 и 4). Для разнополярных напряжений эти два параметра различны. Так известно, что для гармонического напряжения 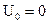 . Рассчитаем
. Рассчитаем 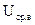 для такого сигнала:
для такого сигнала:
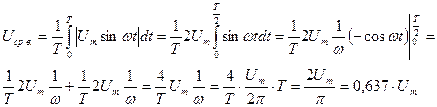
 |
Следовательно, для гармонического сигнала при
двухполупериодном выпрямлении 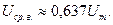
Среднеквадратическим (действующим ) значением напряжения является корень квадратный из среднего значения квадрата мгновенных значений
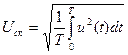 . (5)
. (5)
Подставляя 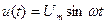 в формулу (5) и используя подстановку
в формулу (5) и используя подстановку 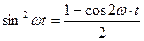 можно получить для гармонического сигнала
можно получить для гармонического сигнала 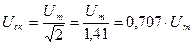 .
.
 2015-07-14
2015-07-14 731
731








