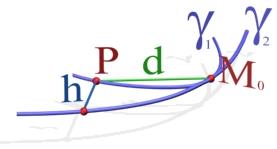
 Пусть
Пусть 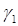 и
и 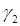 две плоские кривые с параметризациями
две плоские кривые с параметризациями 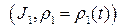 и
и 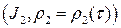 соответственно. Пусть
соответственно. Пусть 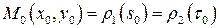 ,
, 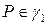 ,
,  - расстояние от точки
- расстояние от точки 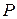 до
до 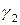 ,
, 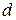 ‑ расстояние то
‑ расстояние то 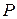 до точки
до точки 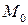 .
.
Определение 12.1. Будем говорить, что кривая 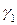 имеет с кривой
имеет с кривой 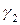 в точке
в точке 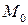 порядок соприкосновения (касания)
порядок соприкосновения (касания) 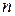 , если
, если 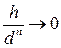 при
при 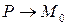 .
.
Теорема 12.1. Пусть кривая 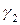 задана неявно уравнением
задана неявно уравнением 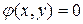 , а кривая
, а кривая 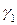 в окрестности точки
в окрестности точки 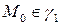 имеет параметризацию
имеет параметризацию 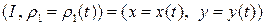 , причем
, причем 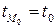 . Для того, чтобы
. Для того, чтобы 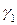 имела с кривой
имела с кривой 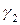 в точке
в точке 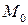 порядок соприкосновения
порядок соприкосновения 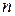 необходимо и достаточно выполнения следующих условий:
необходимо и достаточно выполнения следующих условий:
1. 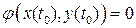 , (то есть
, (то есть 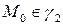 ),
),
2. 
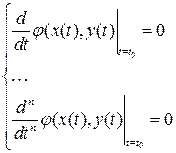
 Доказательство.
Доказательство.
Будем считать, что 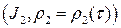 ‑ параметризация некоторой окрестности точки
‑ параметризация некоторой окрестности точки 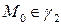
Пусть 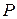 ‑ точка на кривой
‑ точка на кривой 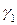 , достаточно (чтобы вести дальнейшие рассуждения без дополнительных оговорок и комментариев) близкая к
, достаточно (чтобы вести дальнейшие рассуждения без дополнительных оговорок и комментариев) близкая к 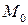 . Обозначим
. Обозначим 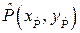 такую точку на кривой
такую точку на кривой 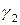 , что расстояние от
, что расстояние от 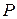 до кривой
до кривой 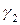 равно расстоянию
равно расстоянию 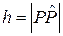 между точками
между точками 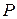 и
и 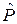 .
.
Покажем, что вектор 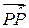 направлен по нормали кривой
направлен по нормали кривой 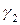 в точке
в точке 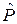 . В самом деле, значение параметра
. В самом деле, значение параметра 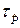 есть точка минимума функции рассмотрим функцию
есть точка минимума функции рассмотрим функцию 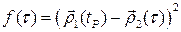 . Значение параметра
. Значение параметра 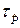 есть точка минимума функции
есть точка минимума функции 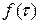 , то есть является решением уравнения
, то есть является решением уравнения 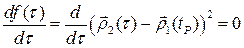 или
или 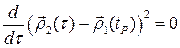 .
.
Но
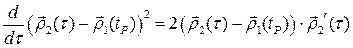 ,
,
поэтому
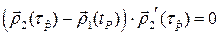
или в других обозначениях 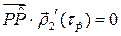 . Последнее равенство говорит о том, что вектор
. Последнее равенство говорит о том, что вектор 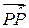 идет перпендикулярно касакасательной кривой
идет перпендикулярно касакасательной кривой 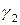 в точке
в точке 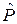 , а значит он сонаправлен с вектором
, а значит он сонаправлен с вектором 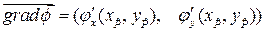 .
.
Если 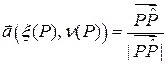 , то
, то 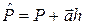 или
или 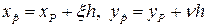 . Кроме того, при
. Кроме того, при 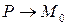 имеем
имеем 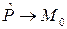 , и вектор
, и вектор 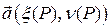 , сохраняя единичную длину, стремится к вектору
, сохраняя единичную длину, стремится к вектору 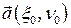 , сонаправленному с
, сонаправленному с  .
.
Это значит, что
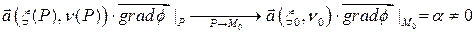 , откуда следует, что, если
, откуда следует, что, если 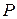 находится достаточно близко к
находится достаточно близко к 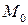 , то
, то

(хвост последовательности 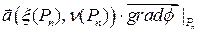 попадает в малую окрестность отличного от нуля числа
попадает в малую окрестность отличного от нуля числа 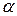 ).
).
Вспомним, что 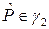 , поэтому
, поэтому 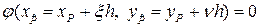 . Разлагая в ряд левую часть последнего равенства, получаем
. Разлагая в ряд левую часть последнего равенства, получаем
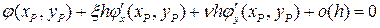
или
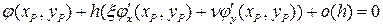
При 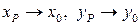 величина
величина 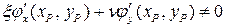 как скалярное произведение сонаправленных ненулевых векторов, поэтому в силу равенства
как скалярное произведение сонаправленных ненулевых векторов, поэтому в силу равенства
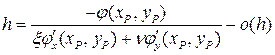
заключаем, что 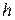 и
и 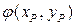 имеют одинаковый порядок малости.
имеют одинаковый порядок малости.
Теперь заметим, что
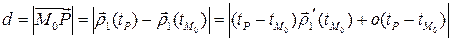 ,
,
то есть 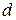 имеет порядок малости такой же, как и
имеет порядок малости такой же, как и 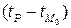 . Следовательно
. Следовательно
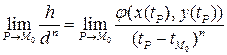 .
.
Правая часть равенства равна нулю тогда и только тогда, когда все члены разложения функции 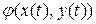 по степеням
по степеням 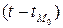 до
до 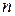 -ого включительно равны нулю, что и доказывает теорему.
-ого включительно равны нулю, что и доказывает теорему. 
Для самостоятельной работы:
 2015-07-14
2015-07-14 653
653








