Определение 15.1. Кривая 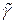 , для которой кривая
, для которой кривая 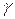 является эволютой, называется ее (кривой
является эволютой, называется ее (кривой 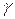 ) эвольвентой.
) эвольвентой.
Уравнение эвольвенты.
Пусть 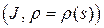 натуральная параметризация кривой
натуральная параметризация кривой 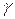 . Будем искать параметризацию эвольвенты
. Будем искать параметризацию эвольвенты 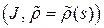 такую, что точка
такую, что точка 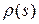 является точкой касания кривой
является точкой касания кривой 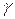 и нормали
и нормали 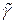 , проходящей через
, проходящей через 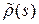 (см. следствие 14.1), то есть положим:
(см. следствие 14.1), то есть положим:
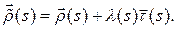
Дифференцируя, получаем
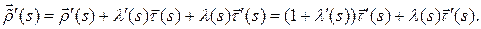
Умножим скалярно обе части равенства на 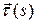 :
:
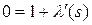
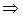
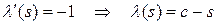 .
.
Таким образом, уравнение эвольвенты в натуральном параметре примет вид:
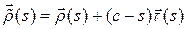 ,
,
где 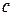 ‑ произвольная постоянная.
‑ произвольная постоянная.
Переходя к произвольной параметризации 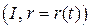 , получим:
, получим:
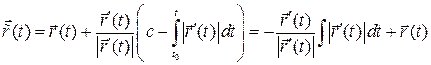
 2015-07-14
2015-07-14 298
298







