1. Если гладкое отображение 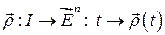 имеет координатное выражение (см.)
имеет координатное выражение (см.)
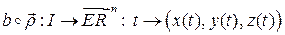 ,
,
то вектор 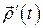 будет иметь координаты
будет иметь координаты 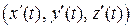 , то есть
, то есть
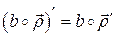 .
.
Применив к обеим частям равенства отображение 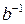 , получим
, получим
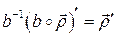
2. Если 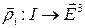 ,
, 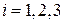 , – гладкие вектор-функции, то
, – гладкие вектор-функции, то
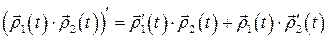 ,
,
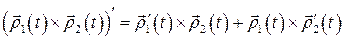 ,
,
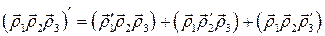 ,
,
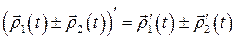 ,
,
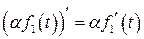 ,
,  .
.
Лемма 1.1. (о вектор-функции постоянной длины)
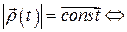
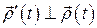 ,
, 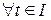 .
.
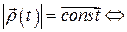
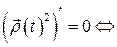

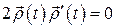 .
. 
Определение 1.1. Отображение 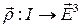 называется регулярным в
называется регулярным в 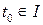 , если
, если 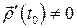 . Говорят, что
. Говорят, что 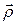 – регулярно, если оно регулярно в любой точке из
– регулярно, если оно регулярно в любой точке из 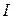 .
.
Отображение 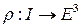 называется непрерывным (гладким класса Ck или регулярным), если таковой является вектор-функция
называется непрерывным (гладким класса Ck или регулярным), если таковой является вектор-функция 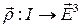 (см.). Соответственно и здесь все сводится к свойствам координатных функций.
(см.). Соответственно и здесь все сводится к свойствам координатных функций.
§2. Определение кривой
Кривая, вообще говоря, есть термин из общеразговорного вокабуляра. Чаще всего этим термином обозначают фигуру в 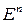
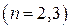 , которую можно представить как траекторию материальной точки в
, которую можно представить как траекторию материальной точки в 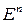 или как изогнутый промежуток, помещенный в
или как изогнутый промежуток, помещенный в 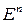 . И то и другое представление математически описывается как образ отображения вида
. И то и другое представление математически описывается как образ отображения вида 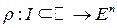 или, используя координатное выражение (для n = 3),
или, используя координатное выражение (для n = 3),
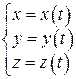
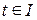 .
.
Выводя из рассмотрения некоторые особые случаи, зададим ограничения на отображение 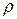 . Начнем с того, что потребуем от
. Начнем с того, что потребуем от 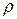 гладкости (это чтобы применять методы анализа).
гладкости (это чтобы применять методы анализа).
Далее, будем считать, что
o 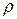 – инъективное (биективное на образ) отображение (исключаем самопересечения);
– инъективное (биективное на образ) отображение (исключаем самопересечения);
o
 |
|
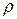 ‑ регулярное отображение (таким образом, мы выводим из рассмотрения фигуры вида
‑ регулярное отображение (таким образом, мы выводим из рассмотрения фигуры вида
o 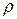 ‑ взаимнонепрерывное отображение.
‑ взаимнонепрерывное отображение.
Смысл последнего ограничения следующий.
Для инъективного (биективного на образ) отображения 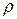 обозначим символом
обозначим символом 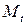 точку, в которую мы попадаем при значении параметра
точку, в которую мы попадаем при значении параметра 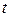 , то есть
, то есть 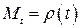 . Аналогично, пусть
. Аналогично, пусть 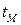 – такое значение параметра
– такое значение параметра 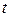 , при котором мы получаем точку
, при котором мы получаем точку 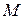 , т.е.
, т.е. 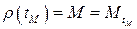 .
.
Определение 2.1. Будем говорить, что инъективное отображение 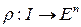 взаимно непрерывно, если любая точка
взаимно непрерывно, если любая точка 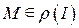 обладает следующим свойством: для любой последовательности
обладает следующим свойством: для любой последовательности 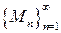 точек в
точек в 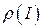 , стремящейся к
, стремящейся к 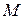 , последовательность
, последовательность 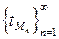 стремится к
стремится к 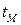 , т.е.
, т.е. 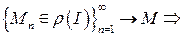
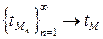 .
.
Определение 2.2. Если 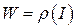 , где
, где 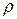 – непрерывное и взаимно непрерывное отображение, то
– непрерывное и взаимно непрерывное отображение, то  называют гомеоморфным образом интервала
называют гомеоморфным образом интервала 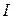 , а само
, а само 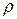 – гомеоморфным отображением (на образ) или гомеоморфизмом (на образ).
– гомеоморфным отображением (на образ) или гомеоморфизмом (на образ).
|
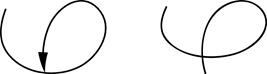 |
не могут быть гомеоморфными образами интервала.
Определение 2.3. Фигура 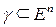 называется кривой, если для любой точки
называется кривой, если для любой точки 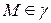 существует окрестность
существует окрестность  в
в 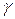 и отображение
и отображение 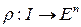 такое, что:
такое, что:
1. 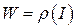 гомеоморфный образ
гомеоморфный образ 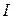 ,
,
2. 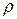 – гладкое регулярное отображение
– гладкое регулярное отображение
При этом пару 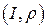 будем называть параметризацией окрестности
будем называть параметризацией окрестности  в
в 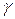
Таким образом, кривая – это фигура, как бы склеенная из деформированных без склеек и разрывов интервалов, на каждом таком интервале определена параметризация, причем параметр играет роль координаты.
Определение 2.4. Отображение 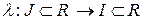 называется диффеоморфизмом, если
называется диффеоморфизмом, если
o 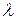 биективно (значит, существует обратное отображение
биективно (значит, существует обратное отображение 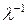 ),
),
o 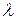 и
и 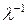 дифференцируемы,
дифференцируемы,
Производная диффеоморфизма нигде не обращается в ноль и, следовательно, имеет постоянный знак, то есть диффеоморфизм – монотонная функция.
Теорема 2.1. Пусть 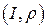 ‑ параметризация окрестности
‑ параметризация окрестности  ,
, 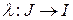 – диффеоморфизм интервала
– диффеоморфизм интервала 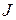 на
на 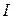 . Тогда
. Тогда 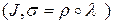 – есть также параметризация
– есть также параметризация  .
.
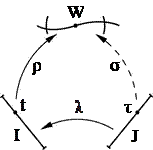
 ►Являясь композицией инъективных гладких отображений
►Являясь композицией инъективных гладких отображений 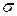 ‑ инъективное гладкое отображение. Далее, так как ρ – взаимнонепрерывно, а
‑ инъективное гладкое отображение. Далее, так как ρ – взаимнонепрерывно, а 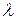 вместе с
вместе с 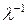 непрерывно, то
непрерывно, то
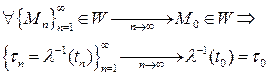
(здесь 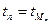 и
и 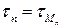 ). Таким образом,
). Таким образом, 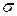 ‑ взаимнонепрерывное отображение. Отображение
‑ взаимнонепрерывное отображение. Отображение 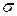 является регулярным. В самом деле:
является регулярным. В самом деле:
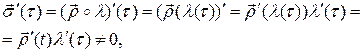
|
так как 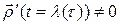 и
и 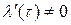 при всех значениях параметра.◄
при всех значениях параметра.◄
Теорема 2.1 говорит о том, как, зная одну из параметризаций окрестности на кривой, построить другие параметризации этой же окрестности. В следующей теореме утверждается, что так получаются все параметризации этой окрестности.
Теорема 2.2. Пусть 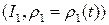 и
и 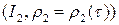 две параметризации одной и той же окрестности
две параметризации одной и той же окрестности  в
в 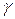 . Тогда существует диффеоморфизм
. Тогда существует диффеоморфизм 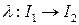 , такой что
, такой что 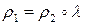 .
.
► 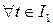 условие
условие 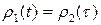 единственным образом определяет точку
единственным образом определяет точку 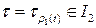 . Другими словами, мы имеем отображение
. Другими словами, мы имеем отображение 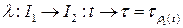 .
.
Так как
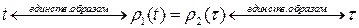 ,
,
то 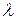 – биекция и
– биекция и 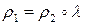 .
.
Для 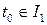 докажем гладкость отображения
докажем гладкость отображения 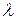 в точке
в точке 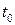 , представив его в виде композиции гладких в некоторой окрестности точки
, представив его в виде композиции гладких в некоторой окрестности точки 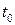 отображений.
отображений.
Обозначим 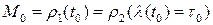 , при этом, в силу регулярности,
, при этом, в силу регулярности, 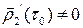 . Для координатных выражений:
. Для координатных выражений:
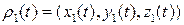 =
= 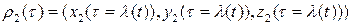
не ограничивая общности, можно считать, что 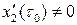 . Если
. Если 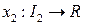 , то
, то 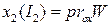 (проекция на ось
(проекция на ось 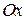 окрестности
окрестности  ).
).
По теореме об обратной функции 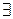 окрестность
окрестность 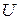 точки
точки 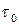 в
в 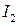 и окрестность
и окрестность 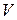 точки
точки 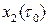 в
в 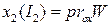 такие, что
такие, что 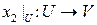 ‑ диффеоморфизм. Это означает, что отображение
‑ диффеоморфизм. Это означает, что отображение 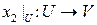 биективно и гладко вместе со своим обратным отображением
биективно и гладко вместе со своим обратным отображением 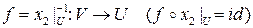 .
.
Положим
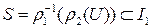 ,
,
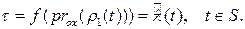
Очевидно, отображение 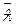 гладко как композиция гладких отображений. Кроме того
гладко как композиция гладких отображений. Кроме того
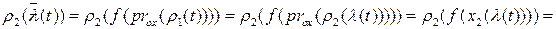
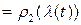 для
для 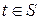 ,
,
откуда, в силу инъективности отображения 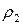 , следует равенство
, следует равенство 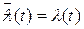 , а, следовательно, и гладкость
, а, следовательно, и гладкость 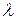 .
.
Аналогично доказывается гладкость 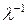 .◄
.◄
Определение 2.5. Диффеоморфизм 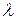 из теоремы 2.2 будем называть заменой параметра.
из теоремы 2.2 будем называть заменой параметра.
Эквивалентность регулярных вектор-функций.
Пусть 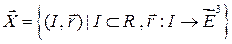 , ‑ множество регулярных вектор-функций. Определим на
, ‑ множество регулярных вектор-функций. Определим на 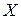 отношение
отношение 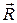 :
:
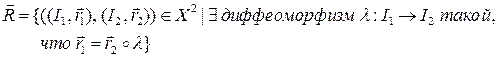
Упражнение 2.2. Отношение 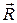 является отношением эквивалентности.
является отношением эквивалентности.
Упражнение 2.3. Эквивалентные вектор-функции имеют совпадающие годографы, однако из совпадения годографов не следует эквивалентность вектор-функций.
Для регулярной вектор-функции 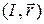 пару
пару 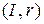 , где
, где 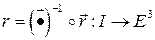 (см. лекцию 1), будем называть параметризованной кривой (не путать с параметризацией кривой). На множестве
(см. лекцию 1), будем называть параметризованной кривой (не путать с параметризацией кривой). На множестве 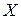 параметризованных кривых также определяется отношение эквивалентности
параметризованных кривых также определяется отношение эквивалентности 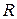 : параметризованная кривая
: параметризованная кривая 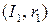 находится в отношении
находится в отношении 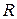 с параметризованной кривой
с параметризованной кривой 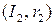 , если существует диффеоморфизм
, если существует диффеоморфизм 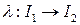 такой, что
такой, что 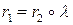 .
.
Теорему 2.2 можно переформулировать следующим образом.
Теорема 2.2’. Любые две параметризации одной и той же окрестности на кривой эквивалентны.
§3. Натуральная параметризация
Теорема 3.1. Пусть 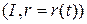 параметризация окрестности
параметризация окрестности  на кривой
на кривой 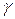 . Существует параметризация окрестности
. Существует параметризация окрестности 
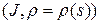 , такая что
, такая что 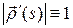 .
.
► Предварительные рассуждения. Если бы это было так, то, дифференцируя равенство 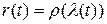 , где
, где 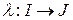 замена параметра, мы бы получили
замена параметра, мы бы получили 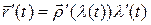 . Переходя к модулям (считая, не ограничивая общности, что
. Переходя к модулям (считая, не ограничивая общности, что 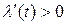 ) ‑
) ‑ 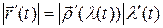 и учитывая требование
и учитывая требование 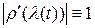 , мы получаем условие, которому должна была бы удовлетворять замена параметра:
, мы получаем условие, которому должна была бы удовлетворять замена параметра: 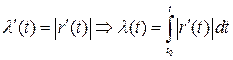 .
.
Перейдем непосредственно к доказательству. Определим
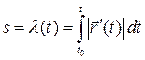 .
.
Являясь интегралом с переменным верхним пределом и положительным подынтегральным выражением, определенная на интервале  функция
функция 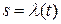 ‑ монотонно возрастающая и дифференцируемая, и, следовательно, является диффеоморфизмом. При этом
‑ монотонно возрастающая и дифференцируемая, и, следовательно, является диффеоморфизмом. При этом 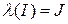 ‑ открытый интервал.
‑ открытый интервал.
Положим 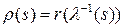 .
.
Докажем, что пара 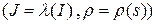 ‑ искомая параметризация окрестности
‑ искомая параметризация окрестности  . В самом деле,
. В самом деле, 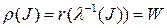 ,
, 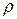 ‑ композиция гладких инъекций
‑ композиция гладких инъекций 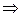 гладкая инъекция.
гладкая инъекция.
Пусть 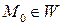 и
и 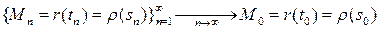 . Тогда
. Тогда 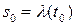 . Кроме того,
. Кроме того, 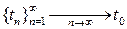 в силу взаимной непрерывности
в силу взаимной непрерывности 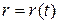 . Так как
. Так как 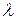 ‑ непрерывно, то
‑ непрерывно, то 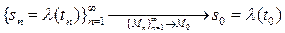 , что доказывает взаимную непрерывность
, что доказывает взаимную непрерывность 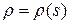 .
.
Учитывая, что 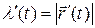 , получаем
, получаем 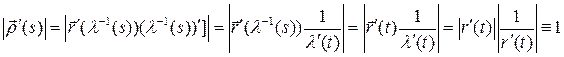 .◄
.◄
Определение 3.1. Параметризация 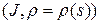 окрестности
окрестности  на кривой
на кривой 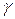 такая, что
такая, что 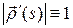 , называется натуральной параметризацией (н-параметризацией).
, называется натуральной параметризацией (н-параметризацией).
Теорема 3.2. Пусть 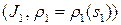 и
и 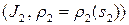 ‑ две натуральные параметризации одной и той же окрестности
‑ две натуральные параметризации одной и той же окрестности  на кривой
на кривой 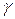 . Тогда замена параметра имеет вид:
. Тогда замена параметра имеет вид: 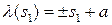 , где
, где 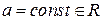 . Наоборот: если
. Наоборот: если 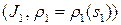 ‑ натуральная параметризация и
‑ натуральная параметризация и 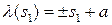 , где
, где 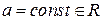 , то
, то 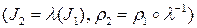 ‑ также натуральная параметризация.
‑ также натуральная параметризация.
►Докажем только первое утверждение.
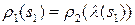
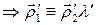
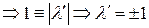 ,
, 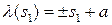 . ◄
. ◄
§4. Способы задания кривых
1.Параметрический.
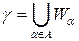 ,
, 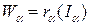 ‑ кривая задается как объединение окрестностей, каждая из которых параметризована.
‑ кривая задается как объединение окрестностей, каждая из которых параметризована.
2. Явный способ задания плоской кривой: график гладкой функции является кривой. В самом деле, пусть 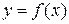 , где
, где 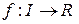 ‑ гладкая функция, определенная на интервале
‑ гладкая функция, определенная на интервале 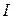 . График этой функции имеет вид:
. График этой функции имеет вид: 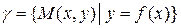 . Это не что иное, как годограф вектор-функции
. Это не что иное, как годограф вектор-функции 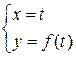 ,
, 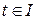 , которая удовлетворяет всем свойствам параметризации. Здесь в качестве параметризованной окрестности
, которая удовлетворяет всем свойствам параметризации. Здесь в качестве параметризованной окрестности  выступает вся фигура
выступает вся фигура 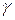 . В такой ситуации говорят, что
. В такой ситуации говорят, что 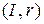 ‑ глобальная параметризация кривой
‑ глобальная параметризация кривой 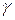 .
.
Упражнение 4.1. Доказать, что окружность является кривой, которая не может быть глобально параметризована.
3. Неявный способ задания плоской кривой.
Пусть 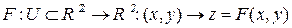 гладкое отображение, заданное в области
гладкое отображение, заданное в области 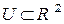 , и
, и 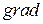
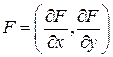 .
.
Если 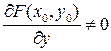 , то, по теореме о неявной функции, существуют окрестности
, то, по теореме о неявной функции, существуют окрестности 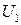 и
и 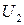 точек
точек 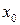 и
и 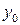 в
в 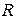 и гладкое отображение
и гладкое отображение 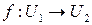 такие, что
такие, что 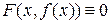 (для
(для 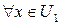 ). Следовательно,
). Следовательно,  состоит из точек
состоит из точек 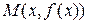 , то есть является графиком функции
, то есть является графиком функции 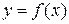 . Таким образом, множество точек
. Таким образом, множество точек 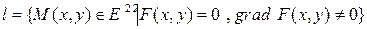 есть кривая.
есть кривая.
4. Неявный способ задания кривой в пространстве.
Пусть 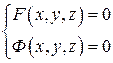 , где
, где 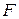 и
и 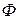 гладкие функции 3-х переменных, заданные в некоторой области
гладкие функции 3-х переменных, заданные в некоторой области 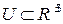 .
.
Рассуждая, как и в предыдущем пункте, получаем, что фигура
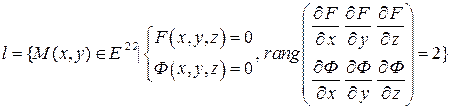 есть кривая.
есть кривая.
§5. Длина дуги кривой.
Пусть 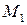 и
и 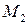 точки из окрестности
точки из окрестности  на кривой
на кривой 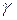 и
и 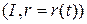 ‑ параметризация
‑ параметризация  .
.
Определение 5.1. Длиной дуги 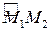 кривой
кривой 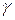 называется число
называется число 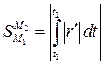 .
.
Если 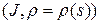 натуральная параметризация окрестности
натуральная параметризация окрестности  , то
, то
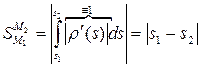 ‑
‑
модуль изменения натурального параметра 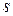 при движении из точки
при движении из точки 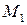 к точке
к точке 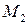 совпадает с длиной дуги кривой между этими точками
совпадает с длиной дуги кривой между этими точками
Упражнение 5.1. Определение 5.1 корректно, то есть не зависит от выбора параметризации.
В дальнейшем будем считать, что 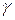 ‑ связное множество (состоит из одного «куска»), то есть не может быть представлено в виде объединения двух непересекающихся открытых множеств. Это, в частности, означает, что
‑ связное множество (состоит из одного «куска»), то есть не может быть представлено в виде объединения двух непересекающихся открытых множеств. Это, в частности, означает, что 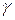 можно задать как образ отрезка при некотором непрерывном отображении.
можно задать как образ отрезка при некотором непрерывном отображении.
Из определения 2.3 следует, что для кривой 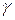 существует семейство окрестностей
существует семейство окрестностей 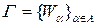 , такое что
, такое что
o 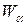 параметризована,
параметризована,
o 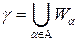 , то есть
, то есть 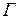 ‑ покрытие кривой
‑ покрытие кривой 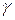 .
.
Так как для произвольных точек 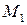 и
и 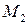 кривой
кривой 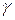 дуга
дуга 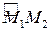 является компактным множеством, в
является компактным множеством, в 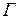 можно выбрать ее (дуги) конечное подпокрытие
можно выбрать ее (дуги) конечное подпокрытие 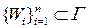 :
: 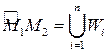 . Пусть
. Пусть 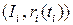 ‑ параметризация
‑ параметризация 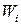 , и для
, и для 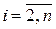
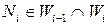 , причем
, причем 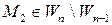 и
и 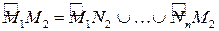 . Тогда длиной дуги
. Тогда длиной дуги 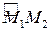 будем называть сумму
будем называть сумму 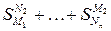 длин дуг, каждая из которых находится в параметризованной окрестности.
длин дуг, каждая из которых находится в параметризованной окрестности.
§6. Репер Френе.
Пусть 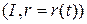 параметризация окрестности
параметризация окрестности  кривой
кривой 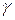 .
.
Определение 6.1. Говорят, что кривая 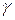 бирегулярна в точке
бирегулярна в точке 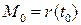 , если
, если
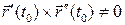
Условие означает неколлинеарность векторов 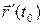 и
и 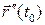 , что эквивалентно условию:
, что эквивалентно условию: 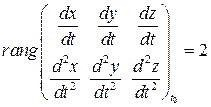 . Кривая называется бирегулярной если она бирегулярна в любой своей точке.
. Кривая называется бирегулярной если она бирегулярна в любой своей точке.
Упражнение 6.1. Определение 6.1 корректно, то есть не зависит от выбора параметризации.
Определение 6.2. Говорят, что кривая 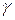 ориентируема, если существует ее покрытие
ориентируема, если существует ее покрытие 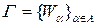 такое, что
такое, что
o 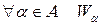 ‑ параметризованная окрестность,
‑ параметризованная окрестность,
o при любых 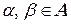 для окрестностей
для окрестностей 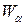 и
и 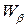 имеем либо
имеем либо 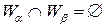 , либо для окрестности
, либо для окрестности 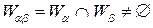 замена параметра
замена параметра 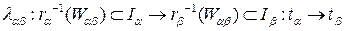 имеет положительную производную.
имеет положительную производную.
Говорят, что кривая ориентирована, если такая параметризация кривой задана (выбрано такое покрытие параметризованными окрестностями, что все замены имеют положительную производную).
 2015-07-14
2015-07-14 533
533