Пусть 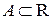 ‑ некоторый интервал и
‑ некоторый интервал и 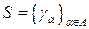 семейство плоских кривых, параметризованное параметром
семейство плоских кривых, параметризованное параметром 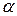 .
.
Определение 13.1. Кривая 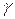 называется огибающей семейства
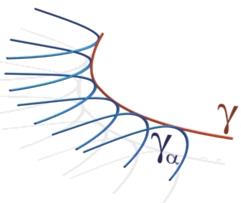
называется огибающей семейства 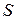 , если она в каждой своей точке касается хотя бы одной кривой семейства, (мы будем рассматривать случай, когда она касается единственной кривой семейства) и каждой своей дугой касается бесконечного множества кривых семейства (порядок касания хотя бы 1).
, если она в каждой своей точке касается хотя бы одной кривой семейства, (мы будем рассматривать случай, когда она касается единственной кривой семейства) и каждой своей дугой касается бесконечного множества кривых семейства (порядок касания хотя бы 1).
Пример. Кривая является огибающей семейства своих касательных.
 Теорема 2. Пусть семейство
Теорема 2. Пусть семейство 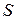 задается уравнением
задается уравнением 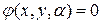 . Тогда огибающая
. Тогда огибающая 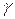 , если она существует, задается уравнением:
, если она существует, задается уравнением:
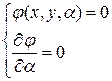
 Будем искать огибающую
Будем искать огибающую 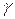 в виде:
в виде: 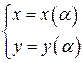 . Это означает, что при любом
. Это означает, что при любом 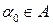 точка с координатами
точка с координатами 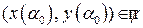 , есть точка касания огибающей
, есть точка касания огибающей 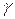 с кривой
с кривой 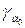 семейства
семейства 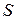 . тогда Тогда
. тогда Тогда 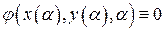 . Дифференцируя по
. Дифференцируя по 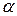 последнее тождество, получаем:
последнее тождество, получаем: 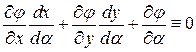 . При
. При 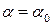 вектор с координатами
вектор с координатами
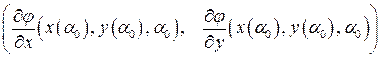
перпендикулярен, как вектор градиента, касательной к кривой 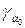 в точке
в точке 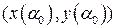 . Точка
. Точка 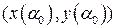 является точкой касания кривой
является точкой касания кривой 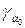 и огибающей
и огибающей 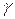 , значит у них в этой точке общие касательные, следовательно, вектор
, значит у них в этой точке общие касательные, следовательно, вектор 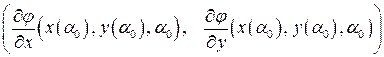 будет перпендикулярен и вектору
будет перпендикулярен и вектору 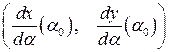 . Так как
. Так как 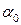 ‑ произвольное значение параметра, то
‑ произвольное значение параметра, то 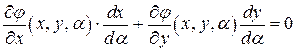 ,, вектор grad идет по нормали т.е. перпендикулярно касательной.
,, вектор grad идет по нормали т.е. перпендикулярно касательной. 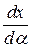 ,
, 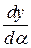 перпендикулярны к огибающей. Значит, скалярное произведение вектора, коллинеарного нормали, и вектора, касательного к кривой,
перпендикулярны к огибающей. Значит, скалярное произведение вектора, коллинеарного нормали, и вектора, касательного к кривой, 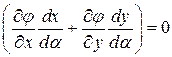 – это есть (вектор коллинеарный нормали к кривой)*(касательный вектор). Значит
– это есть (вектор коллинеарный нормали к кривой)*(касательный вектор). Значит 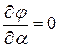 .
. 
 2015-07-14
2015-07-14 454
454








