2015-07-14
690
В дальнейшем будем считать, что в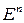 
, где 
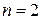или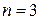 
, зафиксирован правый ортонормированный репер (
).
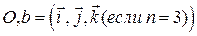Вектор-функции и их годографы.
Упражнение 0.2.
Пусть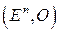 
‑ точечное евклидово пространство с отмеченной точкой (центрированное пространство). Отображение
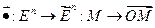
является биекцией.
Отображения
,
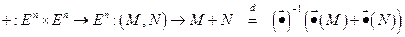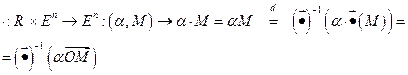
определяют структуру векторного пространства на .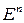
Так как выбор репера центрирует 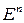, то для любого отображения 
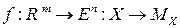существует единственное отображение 
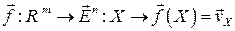, определяемое равенством
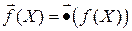
или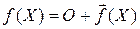 
.
Наоборот, для отображения 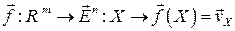равенство
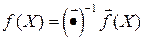
корректно определяет отображение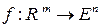 
.
Отображение вида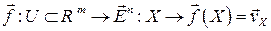 
будем называть вектор-функцией, а множество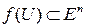 
(см.) ‑ ее годографом. Иногда удобно вектор-функцию воспринимать или задавать как пару 
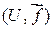, где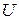 
‑ область определения отображения 
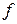. Еще раз подчеркнем, что 
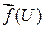‑ фигура в 
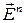, а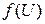 
‑ фигура в .
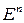Открытые шары и множества.
Фигура
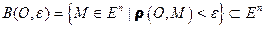
называется открытым шаром радиуса ε с центром в точке О.
Как обычно, под открытым множеством в 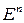будем понимать множество, каждая точка которого принадлежит ему вместе с некоторым открытым шаром.
|
|
|
Пусть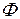 
‑ фигура в 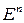. Подмножество 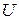в 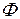будем называть открытым в 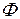, если существует множество 
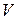, открытое в 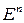, такое, что 
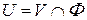. Другими словами, открытыми в 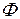являются следы открытых в 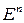множеств и только они. Любое открытое множество, содержащее точку, будем называть окрестностью этой точки.
Открытыми в 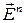множествами будем называть образы открытых множеств в 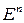при отображении 
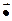(см.)
ГЛАВА 1. КРИВЫЕ.
§1. Некоторые приёмы работы с вектор-функциями
Пусть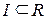 
– интервал, 
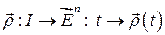‑ вектор-функция. Напомним, что в 
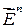предполагается выбранным правый ортонормированный базис.
Координатное выражение вектор-функции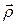 
будет иметь вид
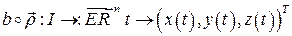или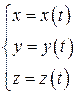 
(рассуждения будем проводить для )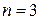
Отображение 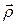будем называть непрерывным (соответственно гладким класса Ck), если координатные функции 
, 
, 
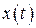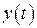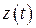непрерывны (соответственно имеют непрерывные производные до k -того порядка включительно).
