Определение 14.1. Эволютой 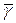 кривой
кривой 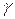 называется фигура, состоящая из центров кривизны этой кривой.
называется фигура, состоящая из центров кривизны этой кривой.
Из определения следует, что, если 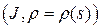 натуральная параметризация кривой
натуральная параметризация кривой 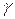 , то уравнение эволюты имеет вид
, то уравнение эволюты имеет вид
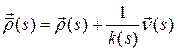
Теорема 14.1. Пусть 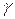 ‑ кривая,
‑ кривая, 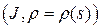 ‑ ее натуральная параметризация, причем
‑ ее натуральная параметризация, причем 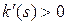 для
для 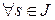 . Длина дуги эволюты между двумя точками равна модулю разности радиусов кривизны кривой в соответствующих точках кривой.
. Длина дуги эволюты между двумя точками равна модулю разности радиусов кривизны кривой в соответствующих точках кривой.
 Найдем длину дуги
Найдем длину дуги 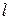 эволюты между точками
эволюты между точками 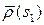 и
и 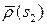 . Для этого сначала подсчитаем вектор
. Для этого сначала подсчитаем вектор 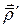 :
:
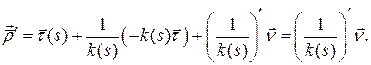
Тогда
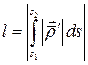
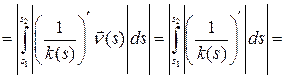
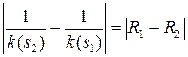 .
. 
Следствие 14.1  Эволюта
Эволюта 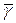 – есть огибающая семейства нормалей кривой
– есть огибающая семейства нормалей кривой 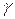 .
.
 Пусть
Пусть 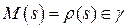 , а
, а 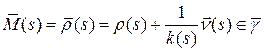 . Будучи точкой эволюты,
. Будучи точкой эволюты, 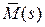 также лежит и на нормали к кривой
также лежит и на нормали к кривой 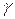 в точке
в точке 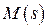 , то есть это общая точка эволюты и соответствующей нормали. При этом вектор
, то есть это общая точка эволюты и соответствующей нормали. При этом вектор 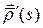 , являющийся направляющим вектором касательной к кривой
, являющийся направляющим вектором касательной к кривой 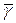 в точке
в точке 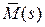 , коллинеарен (главной) нормали к кривой
, коллинеарен (главной) нормали к кривой 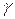 в точке
в точке 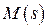 (см.), то есть эволюта касается нормали в точке
(см.), то есть эволюта касается нормали в точке 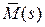 .
.
 2015-07-14
2015-07-14 358
358








