Имеем систему
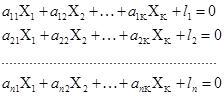
можно записать ее в матричном виде
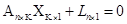
При n > K имеем переопределенную систему, которая может быть как совместной, так и несовместной. Умножив ее на матрицу АТ слева, получим новую систему
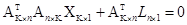 или
или 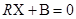
Если rk(A) = K, то можно получить решение
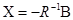 , где
, где 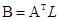
Подставив Х в исходную систему, имеем
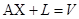
V = 0, если система была совместной. Иначе V обладает свойством VTV = min.
Решение исходной системы можно записать в виде
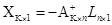
где А+ - главная псевдообратная матрица, удовлетворяющая соотношению
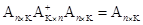 ;
; 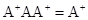 ;
; 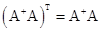 ;
; 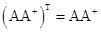
Псевдообратную матрицу можно получить так
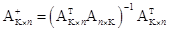
 2015-07-14
2015-07-14 552
552








