Нормой вектора Х называется неотрицательное число ||X||, удовлетворяющее требованиям:
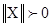 при Х ¹ 0;
при Х ¹ 0;
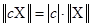 ;
;
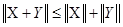 ;
;
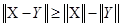 .
.
Для вещественных векторов применяют следующие нормы:
1) Кубическая 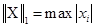 ;
;
2) Октаэдрическая 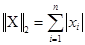 ;
;
3) Сферическая – длина вектора 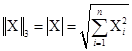
Нормой квадратной матрицы А называется неотрицательное число ||A||, имеющее свойства
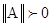 если А ¹ 0;
если А ¹ 0;
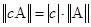 ;
;
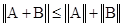 ;
;
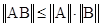 .
.
Рассмотрим нормы матриц
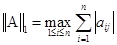
максимальная по строкам сумма модулей элементов матрицы А
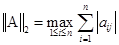
максимальная по строкам сумма модулей элементов матрицы А
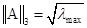
lmax – наибольшее собственное число матрицы АТА.
Числа обусловленности
1) 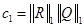
R – матрица нормальных уравнений;
Q = R-1
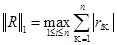
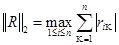
2) Первое число Тюринга
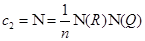
где 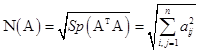
3) Второе число Тюринга
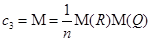
где 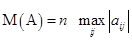
4) Число Тодда
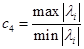
где lI – собственные числа матрицы А
5) 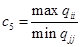
 2015-07-14
2015-07-14 914
914








