Имеем систему уравнений поправок
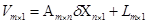
m – количество измерений;
n – число параметров.
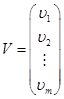 ;
; 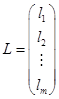 ;
; 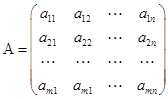 ;
; 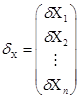
Классический способ: 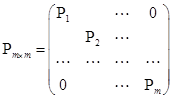 ;
;
Обобщенный способ: 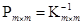 ;
;
Нормальные уравнения: 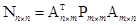 ;
; 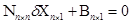 ,
,
где 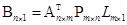 ;
; 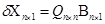 , где
, где 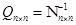 ;
; 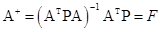
где 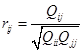 ;
; 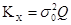 - ковариционная матрица параметров.
- ковариционная матрица параметров.
Блок-схема
 |
1. Даны измерения, их СКО и координаты исходных пунктов.
2. Вычисление Х0 – предварительных значений параметров.
3. Вычисление координат свободных членов уравнений поправок.
4. Составление и решение системы нормальных уравнений: находим dХ.
5. 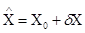 и вычисления уравненных измерений.
и вычисления уравненных измерений.
6. Оценка точности результатов уравнивания.
 2015-07-14
2015-07-14 1023
1023

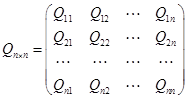 ;
; 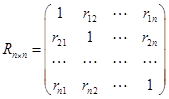 -
- 






