Как правило, геодезические сети привязываются к исходным пунктам, координаты которых принимают безошибочными. Однако эти величины получают из уравнивания и содержат ошибки, которые могут привести к существенным деформациям сети. Поэтому возникает задача уравнивания с учетом ошибок исходных данных.
Пусть:
dХ - параметры для определяемых пунктов;
dZ - параметры для исходных пунктов с матрицей обратных весов исходных данных.
Требуется найти QХ с учетом ошибок исходных данных. Имеем систему уравнений поправок
V1 = AdX + BdZ + L,
V2 = dZ,
где А – матрица коэффициентов уравнений поправок для определяемых пунктов;
В – матрица коэффициентов уравнений поправок для измерений, примыкающих к исходным пунктам, временно считая эти исходные пункты определяемыми. Для случая равноточных измерений имеем систему нормальных уравнений с матрицей
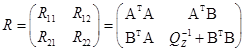 и вектор свободных членов
и вектор свободных членов 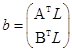
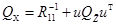 ; причем
; причем 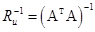
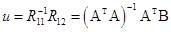
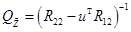 ; где
; где 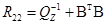
Это способ Маркузе.
Способ Христова
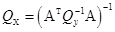 где
где 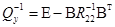
Способ, основанный на фундаментальной теореме
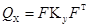 ;
;
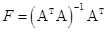 ;
;
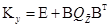 .
.
 2015-07-14
2015-07-14 1329
1329
