Пусть дана функция 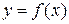 ,
, 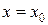 - точка разрыва 1 рода функции
- точка разрыва 1 рода функции 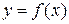 ,
,
если в точке 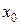 существуют конечные односторонние пределы функции справа и слева т.е.
существуют конечные односторонние пределы функции справа и слева т.е. 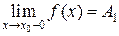 и
и 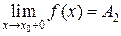 , при этом:
, при этом:
- если
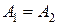 , то точка называется точкой устранимого разрыва 1 рода
, то точка называется точкой устранимого разрыва 1 рода - если
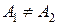 , то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину
, то точка называется точкой конечного разрыва (или неустранимого разрыва) 1 рода. Величину 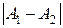 называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
Пример 1: Возьмём 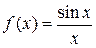 . Все точки области определения
. Все точки области определения 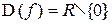 этой элементарной функции являются точками непрерывности. Поскольку
этой элементарной функции являются точками непрерывности. Поскольку 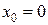 не входит в область определения функции
не входит в область определения функции 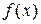 , то 0 - точка разрыва функции
, то 0 - точка разрыва функции 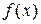 . Мы можем доопределить эту функцию при
. Мы можем доопределить эту функцию при 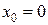 , положив
, положив 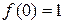 , тогда функция становится непрерывной в точке 0. Значит,
, тогда функция становится непрерывной в точке 0. Значит, 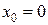 - точка разрыва первого рода для функции.
- точка разрыва первого рода для функции.
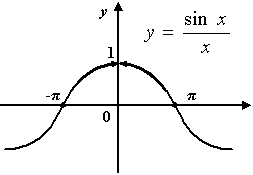
Рис. Устранимый разрыв функции 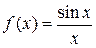
Пример 2: Рассмотрим функцию 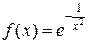 . Её область определения
. Её область определения 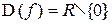 состоит из точек непрерывности, так как это элементарная функция. Точка
состоит из точек непрерывности, так как это элементарная функция. Точка 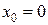 , в которой функция не определена, это точка разрыва функции. Поскольку
, в которой функция не определена, это точка разрыва функции. Поскольку 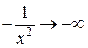 при
при 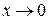 , то
, то 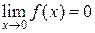 . Это означает, что при
. Это означает, что при 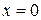 функция имеет устранимый разрыв и становится непрерывной на всей вещественной оси, если положить
функция имеет устранимый разрыв и становится непрерывной на всей вещественной оси, если положить 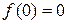 .
.
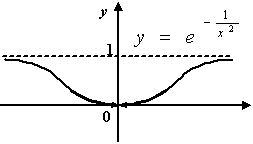
Рис. Устранимый разрыв функции 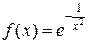
Пример 3: Рассмотрим функцию 
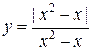 , для которой
, для которой 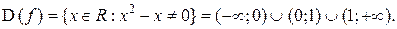 Функция имеет разрывы при
Функция имеет разрывы при 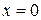 и при
и при 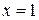 . Распишем модуль разности
. Распишем модуль разности 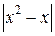 который может быть:
который может быть: 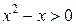 и
и 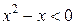 , решением первого неравенства
, решением первого неравенства 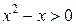 будут 2 интервала
будут 2 интервала 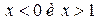 , решением второго
, решением второго 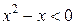 один интервал
один интервал 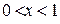 , таким образом
, таким образом 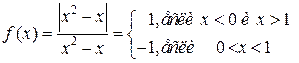
в точках 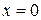 и
и 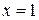 функция имеет неустранимые разрывы первого рода. В точке
функция имеет неустранимые разрывы первого рода. В точке 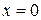 имеем:
имеем: 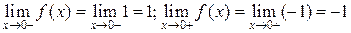 . Таким образом, предельные значения на краях разрыва существуют, но не совпадают; в точке
. Таким образом, предельные значения на краях разрыва существуют, но не совпадают; в точке 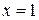 :
: 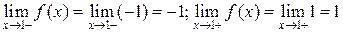 снова пределы слева и справа существуют, конечны, но не совпадают.
снова пределы слева и справа существуют, конечны, но не совпадают.
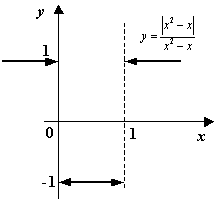
Рис. График функции 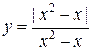 , имеющей точки
, имеющей точки 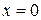 и
и 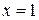 неустранимого разрыва 1 рода, в которых функция делает скачки, величиной
неустранимого разрыва 1 рода, в которых функция делает скачки, величиной 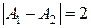
 2015-07-14
2015-07-14 4617
4617
