Пусть дана функция 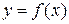 ,
, 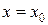 - точка разрыва 2 рода, если по крайне мере один из односторонних пределов (слева или справа) не существует, или равен бесконечности,
- точка разрыва 2 рода, если по крайне мере один из односторонних пределов (слева или справа) не существует, или равен бесконечности,  т.е.
т.е. 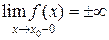 , или
, или 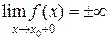 , или
, или 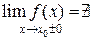
Пример 4: Функция 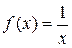 имеет при
имеет при 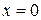 разрыв второго рода, так как
разрыв второго рода, так как 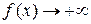 при
при 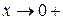 и
и 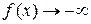 при
при 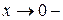 .
.
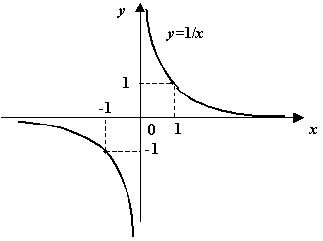
Рис. График функции 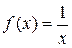
Пример 5: Функция 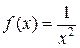 имеет при
имеет при 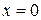 разрыв второго рода, так как
разрыв второго рода, так как 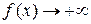 при
при 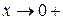 и при
и при 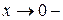 .
.
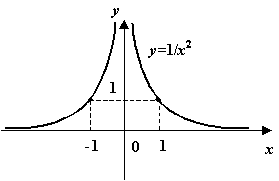
Рис. График функции 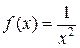
Пример 6: Рассмотрим функцию 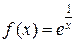 ; её область определения
; её область определения 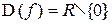 , и точка
, и точка 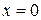 - точка разрыва. Рассмотрим поведение функции слева и справа от точки разрыва. При
- точка разрыва. Рассмотрим поведение функции слева и справа от точки разрыва. При 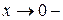 будет
будет  и
и 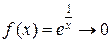 ; при
; при 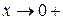 будет
будет 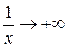 и
и 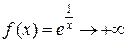 . Итак, значения предела "на правом берегу" разрыва не существует, и разрыв функции
. Итак, значения предела "на правом берегу" разрыва не существует, и разрыв функции 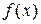 в точке
в точке 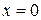 -- второго рода.
-- второго рода.
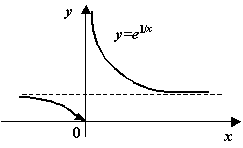
График функции 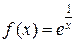
 2015-07-14
2015-07-14 852
852








