Лекция «непрерывность функции. Точки разрыва и их классификация»

Непрерывность функции в точке

ОПРЕДЕЛЕНИЕ 1: Функция 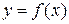называется непрерывной в точке 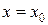, если:

1. функция определена в точке 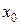и некоторой её окрестности;

2. функция имеет предел при ;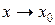

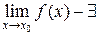3. предел функции при 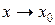совпадает со значениями функции в этой точке,

(1)

Замечание: Так как 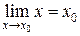, то равенство (1) можно переписать в виде 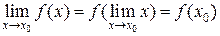, это означает, что при нахождении предела непрерывной функции 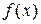можно перейти к пределу под знаком функции, т.е. в функцию 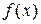вместо аргумента 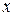подставить его предельное значение .

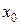Например: 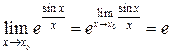. Функция и предел поменялись местами в силу непрерывности функции .

ОПРЕДЕЛЕНИЕ 2: Функция 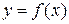называется непрерывной в точке х₀, если её односторонние пределы при 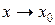равны между собой и совпадают со значением функции в этой точке.

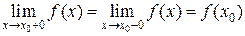(2)

Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.

ОПРЕДЕЛЕНИЕ 3: Функция 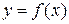называется непрерывной в точке 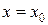, если определена в точке 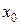и некоторой её окрестности и выполняется равенство: 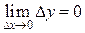, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.