Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.
Теорема 1: Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю)
Теорема 2: Пусть функции 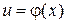 непрерывна в точке
непрерывна в точке 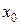 , а функция
, а функция 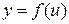 непрерывна в точке
непрерывна в точке 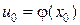 . Тогда сложная функция
. Тогда сложная функция 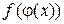 , состоящая из непрерывных функций, непрерывна в точке
, состоящая из непрерывных функций, непрерывна в точке 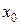 .
.
Теорема 3: Если функция 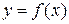 непрерывна и строго монотонна на
непрерывна и строго монотонна на 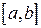 оси
оси 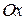 , то обратная функция
, то обратная функция 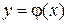 также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке 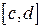 оси
оси 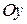 .
.
Все основные элементарные функции непрерывны при всех значениях 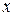 , для которых они определены.
, для которых они определены.
Как известно, элементарной называется функция, которая получена путем применения конечного числа арифметических операций и суперпозиций к основным элементарнымфункциям. Поэтому из вышеприведенных теорем следует, что все элементарные функции, непрерывны в каждой точке, в которой они определены.
Задачи по теме:
1. Исследовать на непрерывность функцию:
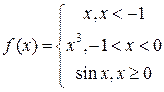
Решение: На каждом из участков области определения функция является непрерывной 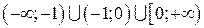 , разрывность в данном случае может наблюдаться только в стыковочных точках, области определения, т.е. в точках, где функция меняет свое аналитическое выражение. Точки
, разрывность в данном случае может наблюдаться только в стыковочных точках, области определения, т.е. в точках, где функция меняет свое аналитическое выражение. Точки 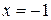 и
и 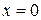 обозначаем как подозрительные на разрыв. Исследовать на разрывность будем, используя аппарат односторонних производных. Найдем пределы справа и слева от точки
обозначаем как подозрительные на разрыв. Исследовать на разрывность будем, используя аппарат односторонних производных. Найдем пределы справа и слева от точки 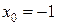 предел слева
предел слева 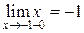 , предел справа
, предел справа 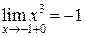 , откуда следует, что функция в данной точке имеет конечные односторонние пределы, значения которых совпадают. В такой ситуации может быть развитие в двух направлениях: 1) возможно функция непрерывна в данной точке, если значение
, откуда следует, что функция в данной точке имеет конечные односторонние пределы, значения которых совпадают. В такой ситуации может быть развитие в двух направлениях: 1) возможно функция непрерывна в данной точке, если значение 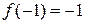 и, следовательно,
и, следовательно, 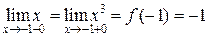 2)
2) 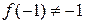 или в данной точке функция просто не определена; и, следовательно,
или в данной точке функция просто не определена; и, следовательно, 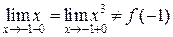 , тогда функция в
, тогда функция в 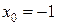 , терпит разрыв 1 рода устранимый.
, терпит разрыв 1 рода устранимый.
Посмотрев на выражение функции, делаем заключение, чтов точке 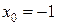 функция не определена и, исходя из выше сказанного, имеет устранимый разрыв 1 рода. Доопределив функцию в этой точке, разрыв устраняется.
функция не определена и, исходя из выше сказанного, имеет устранимый разрыв 1 рода. Доопределив функцию в этой точке, разрыв устраняется.
Исследуем точку 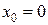 . Найдем пределы справа и слева от точки
. Найдем пределы справа и слева от точки 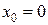 .
. 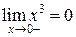 и
и 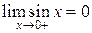 , имеем предыдущую ситуацию, когда значение пределов равны, смотрим значение функции в данной точке:
, имеем предыдущую ситуацию, когда значение пределов равны, смотрим значение функции в данной точке: 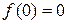 и
и 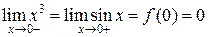 следовательно, согласно второму определению непрерывности функции в точке, сформулированному выше, в данной точке функция непрерывна.
следовательно, согласно второму определению непрерывности функции в точке, сформулированному выше, в данной точке функция непрерывна.
2. Исследовать на непрерывность функцию:
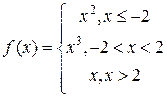
Решение: Обозначаем точки, подозрительные на разрыв: 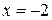 и
и 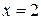 , найдем односторонние пределы:
, найдем односторонние пределы: 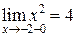 и
и 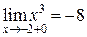 , оба предела конечны, но их значения не равны между собой, следовательно, функция терпит разрыв 1 рода, неустранимый, величина скачка
, оба предела конечны, но их значения не равны между собой, следовательно, функция терпит разрыв 1 рода, неустранимый, величина скачка 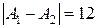 , поскольку предел слева равен значению функции в данной точке, а именно:
, поскольку предел слева равен значению функции в данной точке, а именно: 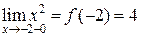 , то функция непрерывна слева. Аналогично находим для
, то функция непрерывна слева. Аналогично находим для 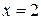 :
: 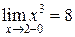 и
и 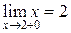 , следовательно, функция терпит разрыв 1 рода, неустранимый, величина скачка
, следовательно, функция терпит разрыв 1 рода, неустранимый, величина скачка 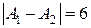 , в силу того, что функция в точке
, в силу того, что функция в точке 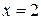 не определена, непрерывности нет ни слева, ни справа.
не определена, непрерывности нет ни слева, ни справа.
3. Исследовать на непрерывность функцию:
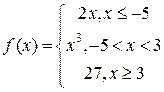
4. Исследовать на непрерывность функцию: 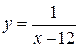
5. Исследовать на непрерывность функцию:
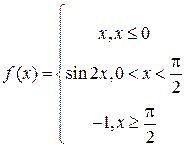
6. Исследовать на непрерывность функцию:
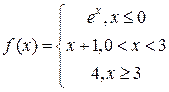
7. Исследовать на непрерывность функцию:
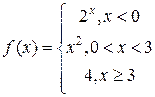
8. Исследовать на непрерывность функцию: 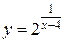
9. Исследовать на непрерывность функцию: 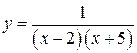
10. Исследовать на непрерывность функцию:
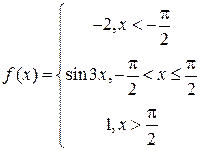
11. Исследовать на непрерывность функцию 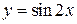 , используя 3 определение:
, используя 3 определение: 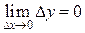
12. Исследовать на непрерывность функцию 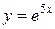 , используя 3 определение:
, используя 3 определение: 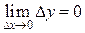
 2015-07-14
2015-07-14 5051
5051