Точки разрыва функции и их классификация

ОПРЕДЕЛЕНИЕ 4: Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Если 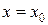- точка разрыва функции 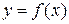, то в ней не выполняется по крайне мере одно из условий первого определения непрерывности функции.

1. Функция определена в окрестности точки 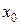, но не определена в самой точке 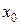. Например: 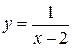не определена в точке .
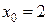2. Функция определена в точке и ее окрестности, но не существует предела 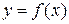при .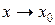

Например: функция 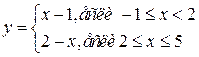определена в точке 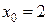, однако в этой точке имеет разрыв, т.к. эта функция не имеет предела при :

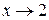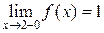и .

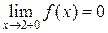1. Функция определена в точке 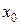и ее окрестности, существует 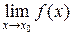, но этот предел не равен значению функции в точке :

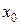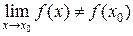
Например: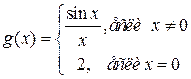

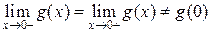
Все точки разрывов функций разделяются на точки разрыва первого и второго рода.