Аналитический метод кинетостатики рассмотрим на примере кривошипно-ползунного и кривошипно-коромыслового механизмов.
Кинетостатический анализ кривошипно-ползунного механизма
Определяем силы, действующие на звенья механизма.
Силы тяжести звеньев:
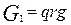 ;
; 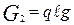 ;
; 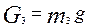 .
.
Силы инерции масс звеньев и их проекции на координатные оси:
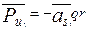 ;
; 
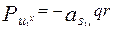 ;
; 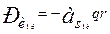 ;
;
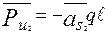 ;
; 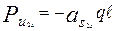 ;
; 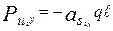 ;
;
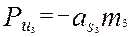 .
.
Момент сил инерции масс шатуна, возникающий при его движении:
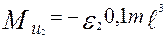 .
.
Для определения реакций в кинематических парах и уравновешивающего момента рассмотрим условия равновесия структурных групп.
Группа звеньев 2-3 (шатун- ползун)
План нагружения группы 2-3 показан на рис. 5.6.
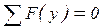 ;
; 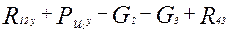 = 0; (5.8)
= 0; (5.8)
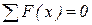 ;
; 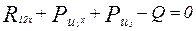 ; (5.9)
; (5.9)
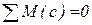 .
.
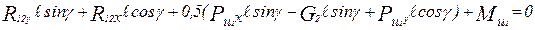 (5.10)
(5.10)
Из (5.10) находим Ŕ12у :
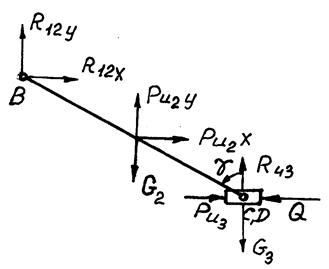
Рис. 5.6
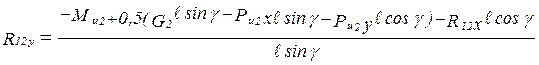 ;
; 
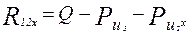 ;
;
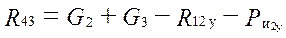 ;
;
Введем ограничение: в соответствии с определением силы полезного сопротивления сила полезного сопротивления Q действует только во время рабочего хода ползуна, т.е. при V c >0.
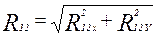 - реакция в кинематической паре В (шатун-кривошип).
- реакция в кинематической паре В (шатун-кривошип).
Реакция в кинематической паре шатун-ползун
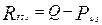 ;
; 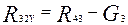 ;
; 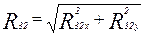 .
.
Входное звено (кривошип)
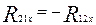 .
. 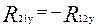 .
.
План нагружений кривошипа приведен на рис.5.7
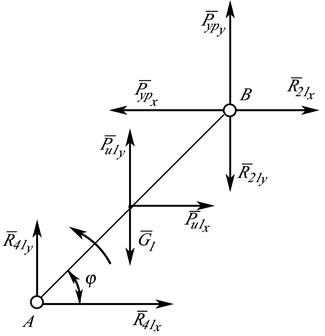
Рис.5.7
Условия равновесия кривошипа:
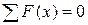 ;
; 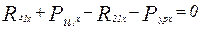 ;
;
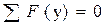 ;
; 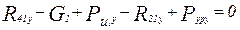 ;
;
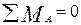 ;
; 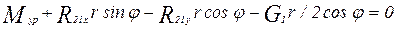 ;
;
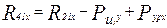 ;
; 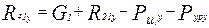 ;
;
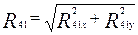 .
.
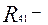 реакция в кинематической паре А (стойка-кривошип)
реакция в кинематической паре А (стойка-кривошип)
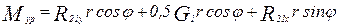 .
.
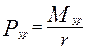 ;
; 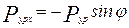 ;
; 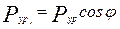 .
.
Определим уравновешивающий момент методом проф. Н.Е. Жуковского ( 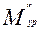 ):
):
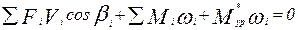 ,
,
где w 1 - угловая скорость кривошипа;
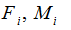 - силы и моменты сил, действующие на i звено;
- силы и моменты сил, действующие на i звено;
Vi - скорость точки приложения i–ой силы;
w i - угловая скорость i–го звена;
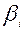 - угол между вектором i–й силы и скоростью точки ее приложения;
- угол между вектором i–й силы и скоростью точки ее приложения;
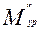 - уравновешивающий момент, приложенный к кривошипу.
- уравновешивающий момент, приложенный к кривошипу.
Первое слагаемое удобно представить как сумму произведений проекций сил и скоростей точек их приложения на координатные оси. Тогда
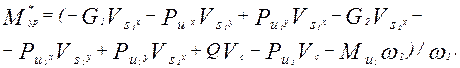

Рассчитывается погрешность определения уравновешивающего момента из условий равновесия и методом профессора Н.Е. Жуковского
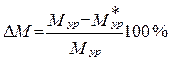 .
.
 2015-07-14
2015-07-14 1034
1034








