Аналитический способ определения передаточного отношения

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь угловую скорость:

1 звено: ω^*₁ = ω₁ + (–ω_н)

2 звено: ω^*₂ = ω^*₃ = ω₂ + (–ω_н)

3 звено: ω^*₃ = ω^*₂ = ω₃ + (–ω_н)

4 звено: ω^*₄ = ω₄ + (–ω_н) = –ω_н

звено H: ω^*_н = ω_н + (–ω_н) = 0

Передаточное число в обращенном движении механизма будет

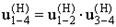(6.65)

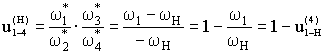(6.66)

Передаточное число планетарного механизма

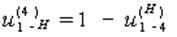(6.67)

Если (6.65) переписать через количество зубьев, то

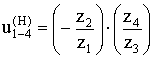(6.68)

Подставив (6.68) в (6.67), получим:

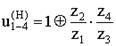- плюсовой механизм (6.69)

Механизм с двумя внутренними зацеплениями (рис.6.31).

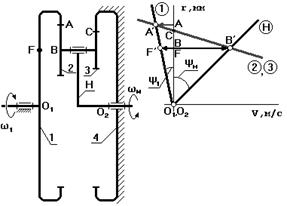
Рис. 6.31

Входное звено – первое колесо;

Выходное – водило.

Графический способ определения передаточного отношения

Выберем точку F на входном звене так, чтобы O ₁ F = O ₂ B.

Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.

ψ₁ и φ₂ – направлены в разные стороны от вертикали. Следовательно, водило Н и колесо 1 вращаются в противоположные стороны.

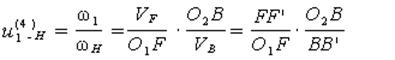(6.70)

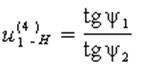(6.71)