Тема 7 кулачковые механизмы

7.1 Общая характеристика кулачковых механизмов.

В самых различных машинах.и приборах для придания исполнительным звеньям движений по строго заданному закону применяются кулачковые механизмы (например, механизм газораспределения в двигателе внутреннего сгорания, механизм подачи инструмента копировального металлообрабатывающего станка и так далее.).Широкое применение кулачковых механизмов обеспечено их относительной простотой, надежностью и компактностью.

Обычно кулачковый механизм состоит из двух подвижных и одного неподвижного (стойка) звеньев. Подвижные звенья образуют со стойкой низшие кинематические пары, а между собой высшую кинематическую пару.

Входное звено - кулачок имеет элементом высшей кинематической пары поверхность переменной кривизны, которая и определяет закон движения выходного звена.

Выходное звено кулачкового механизма, совершающее поступательное движение называется толкателем, а совершающее качательное движение - коромыслом.

На рис 7.1 показаны схемы различных возможных вариантов применяемых кулачковых механизмов.

В зависимости от функционального назначения и особенностей конструкции кулачковые механизмы могут быть плоские с поступательным или вращательным (дисковые) движением кулачка и пространственные (с цилиндрическим, коническим, гиперболоидным и коноидным кулачком).

Непрерывный контакт элементов высшей кинематической пары может обеспечиваться геометрическим замыканием (за счет пазов, охватывающих ролик) или силовым замыканием (за счет сил упругости пружин, давления рабочей жидкости, газа и так далее.).

В контакте рабочих поверхностей подвижных звеньев кулачкового механизма развиваются большие контактные напряжения и силы трения.

Для уменьшения сил трения и изнашивания поверхностей концевая часть выходного звена снабжается роликом или тарелкой (с плоской, цилиндрической или сферической контактной поверхностью).

В транспортных машинах наибольшее применение находят плоские кулачковые механизмы с дисковыми кулачками. В таких механизмах кулачок совершает вращательное движение, а размеры и кривизна его профиля определяют закон движения толкателя или коромысла.

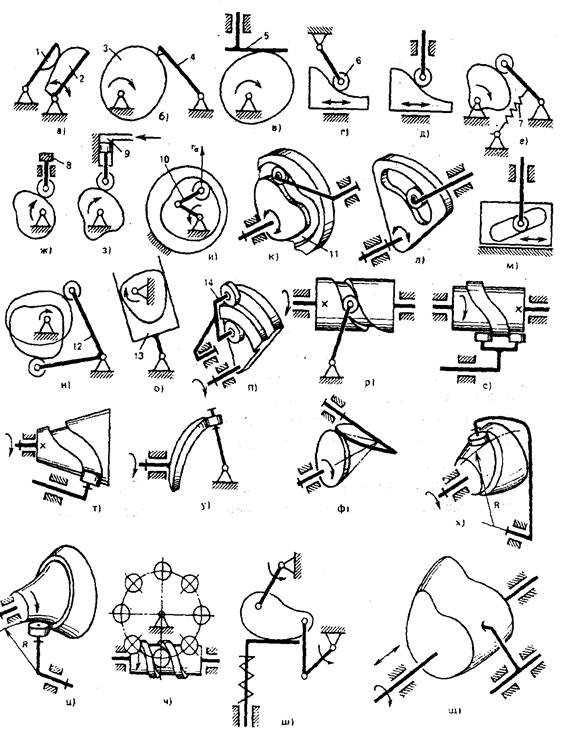
Рис.7.1

Вопросы для самоконтроля:

1. Какой механизм называется кулачковым?

2. Для чего предназначен кулачковый механизм?

3. Как называется выходное звено кулачкового механизма, совершающее возвратно-поступательное движение?

4. Как называется выходное звено кулачкового механизма, совершающее возвратно-вращательное движение?

5. Какие кинематические пары образуют звенья кулачкового механизма?

6. Чем обеспечивается непрерывный контакт звеньев кулачкового механизма?

7. Приведите примеры использования кулачковых механизмов в транспортных машинах.

7.2 Основные геометрические и кинематические параметры механизмов с плоскими дисковыми кулачками.

За цикл работы механизма входное звено (дисковый кулачок) совершает полный оборот, то есть, угол поворота j кулачка равен 2p. Соответственно, выходное звено - толкатель (рис. 7.2а,б), совершая возвратно-поступа-ельное движение и пройдя путь 2S_max, возвращается в свое исходное положение, а выходное звено коромысло (рис. 7.2в) возвращается в свое первоначальное положение, совершив возвратно-вращательное движение вокруг оси вращения на угол, равный 2b_max. Расстояние S_max, которое толкатель проходит из одного крайнего положения в другое, называется ходом толкателя, а угол b_max называется углом размаха коромысла.

Весь период движения толкателя (или коромысла) включает в себя четыре фазы:

- удаление из крайнего ближнего по отношению к центру кулачка положения в крайнее дальнее положение (фаза удаления);

- стояние в крайнем дальнем положении (фаза верхнего выстоя);

- возвращение из крайнего дальнего положения в крайнее ближнее положение (фаза приближения);

- стояние в крайнем ближнем положении (фаза нижнего выстоя).

Углы поворота j кулачка и промежутки времени t, соответствующие этим фазам, имеют следующие обозначения и названия:

Ф₁ и t ₁ - угол и время удаления;

Ф₂ и t ₂ - угол и время верхнего выстоя;

Ф₃ и t ₃ - угол и время приближения;

Ф₄ и t ₄ - угол и время нижнего выстоя.

Очевидно, что

Ф₁+ Ф₂+ Ф₃+ Ф₄ = 2p;

t ₁ + t ₂ + t ₃ + t ₄= Т,

где Т - время одного оборота кулачка.

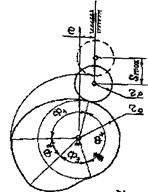
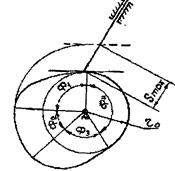
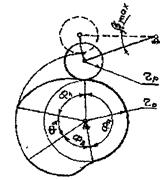
а) б) в)

Рис.7.2

Фазе верхнего выстоя Ф₂ и фазе нижнего выстоя Ф₄ со­ответствуют участки профиля кулачка, представляющие собой окружности с центрами, совпадающими с центром вращения кулачка и радиусами соответственно r _max и r _min, где r _max - максимальное расстояние, а r _min -минимальное расстояние от точек профиля кулачка до его центра вращения. Окружность радиуса r ₀= r _min, центр которой совпадает с центром вращения кулачка, называется основном окружностью кулачка, а соответствующий ей цилиндр — основной шайбой кулачка.

Фазе удаления Ф₁ и фазе приближения Ф₃ соответствуют участки профиля кулачка, представляющие кривые переменной кривизны. Закон движения выходного звена (толкателя или коромысла) в указанных фазах определяется угловой скоростью кулачка и кривизной профиля, соответствующей этим фазам.

При кинематическом и динамическом анализе механизма удобно представить закон движения толкателя в виде кинематических диаграмм функций перемещения S (t) по времени или S (j) по углу поворота кулачка, а так же скорости S'(t) и ускорения S"(t) или их аналогов S'(j) и S"(j).

Вопросы для самоконтроля:

1. Назовите основные кинематические параметры движения звеньев кулачкового механизма.

2. Назовите фазы движения выходного звена кулачкового механизма.

3. Что называется основной окружностью кулачка?

4. Какие участки профиля кулачка соответствуют фазам верхнего и нижнего выстоя?

5. Какие участки профиля кулачка соответствуют фазам удаления и приближения?

6. Чем определяется закон движения выходного звена в фазах удаление и приближения?

7.3 Задачи и критерии синтеза кулачковых механизмов

Основная задача синтеза кулачковых механизмов состоит в определении формы профиля кулачка и его размеров, обеспечивающих при заданных (или выбранных) законах движения кулачка и ведомого звена необходимые геометрические, кинематические и силовые параметры механизма, которые, в свою очередь, задаются технологическими и силовыми условиями его работы (фазовые углыФ_1, Ф_2, Ф_3, Ф₄, ход S _max или угол размаха b_max ведомого звена; угол давления n и другие). К конструкции кулачкового механизма предъявляются так же требования компактности, плавности и бесшумности работы, максимального КПД, прочности и высокой износостойкости элементов кинематических пар.

Кинематические и силовые условия взаимодействия подвижных звеньев кулачкового механизма, а так же его КПД в значительной мере могут характеризоваться углами давления и передачи.

Углом давления n называют острый угол между направлением вектора скорости точки касания выходного звена с кулачком и вектором силы давления кулачка на выходное звено (общей нормалью к профилям этих звеньев в указанной точке) (рис.7.3).

Углом передачи называют угол g = 90° - n, образуемый направлением вектором скорости точки выходного звена, соприкасающейся с кулачком, и общей касательной t-t к профилям этих звеньев в указанной точке.

Из приведенного на рис. 7.3 параллелограмма скоростей получим:

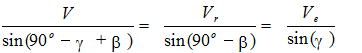(7.1)

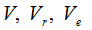где - векторы скоростей точки касания толкателя с

кулачками в абсолютном, относительном и переносном движении;

b - угол между вертикалью и радиус-вектором ` r указанной точки (угол обусловлен наличием эксцентриситета e)

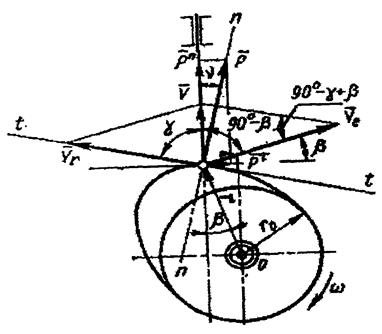
Рис.7.3

Обозначая через w угловую скорость кулачка, получим:

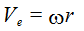(7.2.)

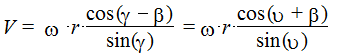(7.3)

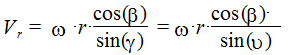(7.4)

Из формулы (7.3) видно, что увеличение угла g передачи (уменьшение угла n давления) с точки зрения кинематики невыгодно, так как можно получить слишком малые скорости движение толкателя, несмотря на большие угловые скорости кулачка. В то же время, как следует из формулы (7.4), увеличение угла g (уменьшение угла n) ведет к уменьшению относительной скорости, что в некоторых конструкциях механизмов может иметь существенное положительное значение.

На рис 7.3 сила ` Р - сила давления кулачка на толкатель, ее составляющие ` Р ⁿ направлена вдоль, а сила ` P ^t - перпендикулярно оси толкателя.

Сила Р ⁿ = Р× соs (n) действует по направлению движения толкателя, а сила Р ^t = Р× sin (n) изгибает толкатель и прижимает его к направляющим, увеличивая силу трения.

Следовательно, уменьшение величины угла n давления (увеличение угла g передачи) благоприятно сказывается на силовом взаимодействии подвижных звеньев. В этом случае уменьшается изгибающее толкатель усилие и силы трения в направляющих толкателя.

Таким образом, определение оптимальных значений углов n и g с учетом противоречивых требований по выполнению кинематических и силовых условий взаимодействия подвижных звеньев представляет собой достаточно сложную задачу. На основании теоретических и экспериментальных исследований рекомендуется принимать для кулачковых механизмов с толкателем n < 30° или g > 60°, для коромысловых кулачковых механизмов n < 45° или g > 45°.

Выбор закона движения выходного звена определяется требованиями плавности и бесшумности работы кулачкового механизма. На рис.7.4 показаны три закона движения толкателя в виде зависимостей S = S (t), V = V (t) и а = а(t) для фазы удаления. Граничные условия заданы: в начале фазы удаления t = 0 и S = 0, в конце фазы t = t ₁, S = S _max. Простейшим законом движения является закон постоянства скорости (кривая 1), при котором максимальная скорость толкателя V _max имеет наименьшее значение.

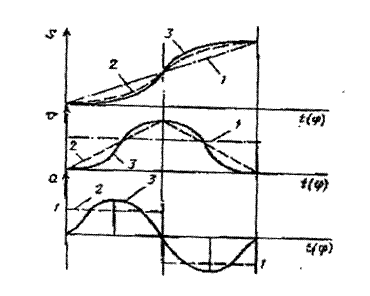
Рис.7.4

Но в начале и конце фазы движения происходят жесткие удары, то есть, скорости толкателя должны получать мгновенные изменения (а ® ¥).

Жестких ударов можно избежать, используя закон постоянного ускорения (кривая 2), при котором толкатель сначала движется равноускоренно, а потом равнозамедленно.

Однако, при переходе от равноускоренного к равнозамедленному движению мгновенно изменяется направление ускорения, а значит, и силы инерции, что называют мягким ударом. Избежать мгновенного изменения ускорения удается применяя закон синусоидального ускорения (кривая 3), а также других.

При синтезе кулачкового механизма закон движения выходного звена обычно задают законом изменения ускорения а = а (t), по которому интегрированием определяют закон изменения скорости V = V(t), а затем вторичным интегрированием - закон перемещений S = S (t).

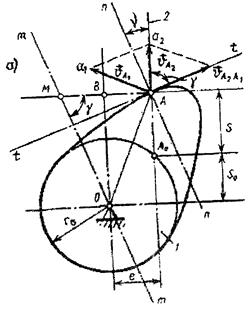
Компактность кулачкового механизма зависит от величины радиуса окружности основной шайбы. Рассмотрим методику расчета радиуса основной окружности кулачка на примере дезаксиального кулачкового механизма с толкателем. На рис 7.5.а показана схема механизма, на которой построен параллелограмм скоростей (план скоростей).

. Дополнительно через точку А проведены нормаль nn и касательная tt, а так же горизонтальная и вертикальная линии. Через точку О проведена линия mm, параллельная нормали nn и на пересечении ее с горизонталью получена точка М.

D ОАМ ~ D Аа₁а₂, а Ð АМО = g.

Так как

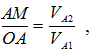то

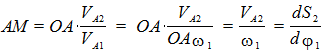
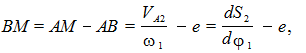
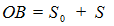
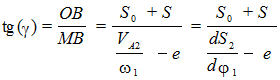(7.5)

Формула (7.5)показывает, что угол передачи g зависит от габаритов кулачка. При уменьшении радиуса r ₀ основной шайбы кулачка уменьшается и расстояние S ₀, а следовательно и угол передачи g.

Для нормальной работы механизма должно соблюдаться условие

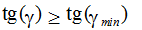
т.е.

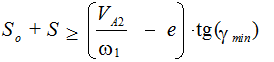
а) б)

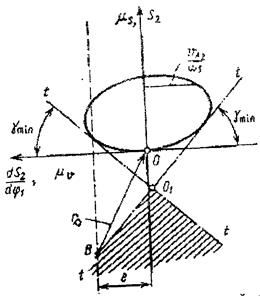
Рис.7.5

или

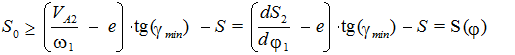(7.6)

Условие (7.6) должно выполняться для любого значения j. Из рис.7.5а следует

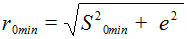(7.7)

Графоаналитический метод определения r _0min состоит в построении

графика

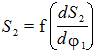(рис.7.5б)

К построенному графику проводятся предельные касательные tt под углом

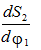
g_min, к оси

Эти касательные продолжаются до их взаимного пересечения. Заштрихованная область, определяемая пересечением предельных касательных, является областью центров вращения кулачков.

При заданном эксцентриситете е радиус r _{0 min} = ВО.

Вопросы для самоконтроля:

1. Назовите основную задачу синтеза кулачкового механизма.

2. Что называется углом давления?

3. Что называется углом передачи?

4. Как влияет изменение угла давления на скорость движения выходного звена?

5. Как влияет изменение угла давления на силовое взаимодействие звеньев кулачкового механизма?

6. Каковы максимально допустимые значения углов давления?

7. Чем характеризуется движение выходного звена при различных законах его движения?

8. В чем состоит графоаналитический метод определения минимального радиуса кулачка?