U(4)1–Н = 1 – u(Н)1–4 (6.76)
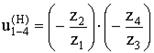 (6.77)
(6.77)
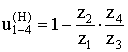 - минусовой механизм.
- минусовой механизм.
6.8.4 Синтез (проектирование) планетарных механизмов.
Под синтезом в этом курсе будем понимать подбор (определение) чисел зубьев планетарных механизмов при условии, что зубчатые колеса нулевые, а радиальный габарит механизма минимальный.
Расчет на прочность не проводим, но он обязательно должен быть проведен при проектировании.
При проектировании конструктор обязан выполнить ряд условий:
1. Отклонение от заданного передаточного отношения не должно превышать 10%.
2. Обеспечить отсутствие подреза у нулевых зубчатых колес:
у колес с внешними зубьями zi ≥ 18;
у колес с внутренними зубьями z ≥ 85.
3.Обеспечить отсутствие заклинивания в зацеплении сателлит – коронная шестерня. Заклинивания нет, если zкш – zсат ≥ 8
4. Обеспечить выполнение условия соосности входного и выходного звеньев.
5. Необходимо обеспечить выполнение условие соседства (окружности вершин соседних сателлитов не должны касаться друг друга).
6. Обеспечить выполнение условия сборки.
Проектирование однорядного планетарного механизма (рис. 6.29) .
Определить: z1, z2, z3 при минимальном радиальном габарите, если дано: u(3)1–Н = 6; m = 1 мм; k = 3 – количество сателлитов; колеса – нулевые.
В соответствии с (6.64)
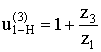
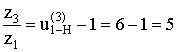
Зададимся числом зубьев z 1 так, чтобы выполнялось условие отсутствие подреза у зубчатых колес, тогда z 1 = 18, z3 = 5 . 18 = 90 ≥ 85.
Условие соосности записывается в виде О 1 В = О 2 В:
r 1 + r 2 = r 3 – r 2 (6.78)
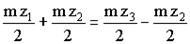
z1 + z2 = z3 – z2
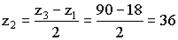
Выполнение условия соседства означает, что окружности вершин соседних сателлитов не касаются друг друга (рис.6.33)
ВIBII > 2 ra2 (6.79)
Рассмотрим треугольник O1BIq: BIBII = 2BIq
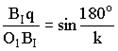
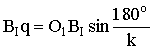
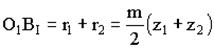
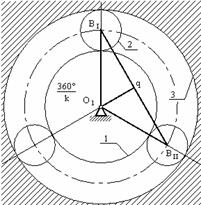
Рис. 6.33
2BIq = BIBII = m(z1 + z2) (6.80)
ra2 = r2 + xm + ha*m – ∆ym
Т.к. колеса нулевые, то xm = 0 и ∆ym = 0
ra2 = r2 + ha*m
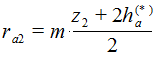
2 r a2 = m (z 2 + 2 h a*) (6.81)
Подставим (6.80), (6.81) в (6.79)
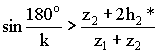 (6.82)
(6.82)
Уравнение соседства справедливо для всех схем, только для схем рис.6.30, 6.31 и 6.32 в знаменателе стоит правая или левая часть условия соосности, а в числителе вместо z2 ставят число зубьев наибольшего из сателлитов.
Рассмотрим условие сборки:
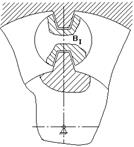
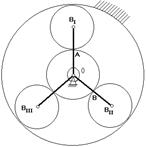
Рис. 6.34
Будем считать, что каждый последующий блок сателлитов устанавливается в позиции ВI.
Чтобы освободить место, нужно повернуть водило на угол (360о / k).
При установке 1 –го сателлита зубья центральных колес ориентированы относительно оси симметрии.
Если на дуге АВ (рис.6.34) укладывается целое число шагов, то при повороте водила на угол (360о/k) зубья центральных колес будут ориентированы относительно оси симметрии точно так же, как и при установке первого сателлита.
Если на указанной дуге не укладывается целое число шагов, то при повороте водила на угол (360о / k) зуб 1 –го колеса не встанет на то же место и тогда, чтобы установить следующий сателлит, нужно от позиции ВII сделать р дополнительных оборотов водила, чтобы за счет выборки углового шага правильно ориентировать зубья центральных колес.
Уравнение сборки имеет вид:
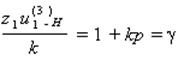
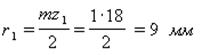
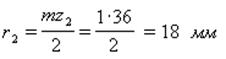
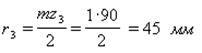
По полученным данным строится схема механизма в масштабе и проверяется выполнение передаточного отношения.
Проектирование планетарного механизма со смешанным зацеплением.
Дано: 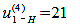 m = 1 мм (Рис.6.35)
m = 1 мм (Рис.6.35)
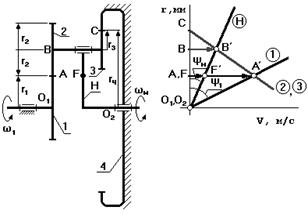
Рис. 6.35
Определить: z 1, z 2, z 3, z 4 при условии: k = 3, и минимальных радиальных габаритах, колеса – нулевые.
Исходная формула:
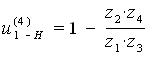
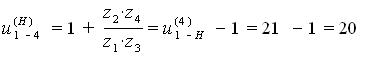
Представим число (20/1) в виде произведений сомножителей:
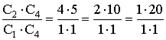 ,
,
где С 1~z1; С 2~z2; С 3~z3; С 4~z4
при этом С 1, С 2, С 3, С 4 – взаимно простые числа, то есть не имеют общих делителей.
Указываются все возможные разложения
С 1 = 4; С 2 = 1; С 3 = 1; С 4 = 5.
Запишем условие соосности данного редуктора О 1 В = О 2 В:
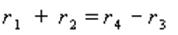
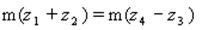
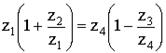
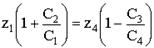
В результате преобразований
z1 = C1 (C4 – C3) q
z4 = C4 (C1 + C2) q
где q – коэффициент пропорциональности – любое число, но такое, чтобы z i было целым.
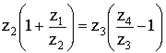
тогда
z2 = C2 (C4 – C3) q
z3 = C3 (C1 + C2) q
q назначается так, чтобы не было подреза ножки зуба, например q = 5
z1 = 1 (5 – 1)q = 4q z1 = 20
z2 = 4 (5 – 1)q = 16q z2 = 80
z3 = 1 (1 + 4)q = 5q z3 = 25
z4 = 5 (1 + 4)q = 25q z4 = 125
Проверяем выполнение условия соседства:
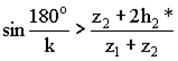
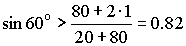
0,87 > 0,82 - условие соседства выполняется.
Проверяем выполнение условия сборки:
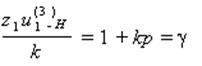 (6.83а)
(6.83а)
20 . 21(1+3p) / 3 = 140 при p = 0
Для передач со сдвоенными сателлитами формула (6.83а) не является общей.
Общей формулой является:
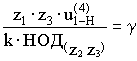 (6.83б)
(6.83б)
где g- целое число,
НОД – наибольший общий делитель z2 и z3
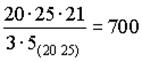
- условие сборки выполняется
Если хотя бы одно из условий не выполняется, то необходимо рассмотреть следующий вариант разложения на простые множители.
Если, перебрав все возможные варианты разложения, не удалось подобрать числа зубьев, то допускается изменить заданное передаточное отношение в пределах 10 %.
Для других схем числа зубьев подбираются по формулам, представленным в таблице:
Таблица 6.3
| Двухрядный механизм со смешанным зацеплением | Двухрядный механизм с двумя внешними зацеплениями | Двухрядный механизм с двумя внутренними зацеплениями |
| z1=C1q(C4 – C3) | z1=C1q(C4 + C3) | z1=C1q(C4 - C3) |
| z2=C2q(C4 – C3) | z2=C2q(C4 + C3) | z2=C2q(C4 - C3) |
| z3=C3q(C1 + C2) | z3=C3q(C1 + C2) | z3=C3q(C1 - C2) |
| z4=C4q(C1 + C2) | z4=C4q(C1 + C2) | z4=C4q(C1 - C2) |
Планетарные механизмы с двумя степенями подвижности (дифференциалы)
Внесем изменение в схему планетарного механизма (схема 1 таблица 6.1) - сделаем колесо 3 подвижным, соединив его вращательной парой со стойкой. Полученный механизм имеет степень подвижности W = 2.
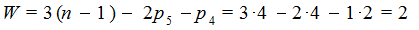
Это означает, что на выходе имеются два независимых движения (звено Н и звено 3), либо из двух независимых движений получают одно определенное движение.
На практике в качестве механизмов с двумя подвижностями наиболее часто применяются планетарные зубчатые механизмы или как их еще называют планетарные дифференциалы. Это название справедливо для механизмов, в которых входной энергетический поток разделяется на два выходных потока. Если входные энергетические потоки суммируются на выходе в один выходной поток, то такие механизмы следует называть суммирующими или интегральными.
Все рассмотренные типовые схемы механизмов можно выполнить с двумя подвижностями. Рассмотрим в качестве примера двухрядный механизм с одним внешним и одним внутренним зацеплением (рис. 6.36).
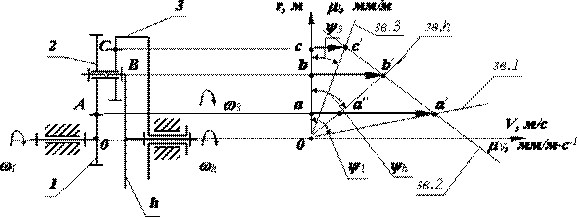
Рис. 6.36
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1
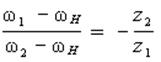
для внутреннего зацепления колес z4 и z3
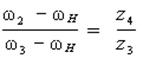
Перемножим, правые и левые части этих уравнений, и получим соотношение между угловыми скоростями механизма с двумя подвижностями
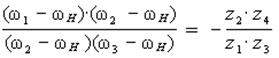
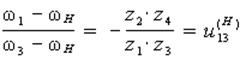
u13 (h) × w 3 - u13 (h) × w h = w 1 - w h
w 1 - (1 + u13 (h)) × w h - u13 (h) × w 3 = 0

Рис. 6.37
Чтобы из механизма с двумя подвижностями получить одноподвижный механизм необходимо либо остановить одно из подвижных звеньев, либо связать между собой функционально (например, простой зубчатой передачей) два подвижных звена. Механизмы, образованные по второму способу, называются замкнутыми дифференциалами. Схема такого механизма приведена на рис.6.37.
Вопросы для самоконтроля:
1. Какой механизм называется планетарным?
2. Какие механизмы относятся к типовым планетарным механизмам?
3. Какое колесо планетарного механизма называется «солнечным»?
4. Какое колесо планетарного механизма называется «короной»?
5. Какие колеса планетарного механизма называются «сателлитами»?
6. Какое звено планетарного механизма называется «водило»?
7. Чему равна степень подвижности планетарного механизма, в котором наряду с подвижными колесами есть колесо, жестко закрепленное со стойкой?
8. Чему равна степень подвижности планетарного механизма, у которого все колеса подвижны?
9. В чем заключается условие соосности планетарных механизмов?
10. В чем состоит условие сборки планетарного механизма?
11. В чем суть условия соседства при синтезе планетарных механизмов?
 2015-07-14
2015-07-14 2256
2256
