Метод последовательных приближений (метод простой итерации)

Заменим исходное уравнение f (x) =0 равносильным уравнением x=j (x). Тогда формула для вычисления последовательных приближений будет выглядеть так:

x_n+1=j (x_n)(n=0, 1, 2,…); где x₀ – начальное приближение, x₀ 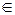[ a, b ].

Приведем достаточное условие сходимости итерационного процесса:

Теорема. Пусть функция j (x) определена и дифференцируема на отрезке

[ a, b ], причем все ее значения j (x) 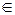[ a, b ]. Тогда, если существует q такая, что

| j¢ (x)| £ q < 1 для всех x 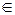[ a, b ],

то процесс итерации x_n+1=j (x_n)(n=0, 1, 2,…) сходится независимо от начального значения x₀ 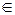[ a, b ] и предельное значение x= 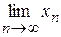является единственным корнем уравнения x=j (x)на отрезке [ a, b ].

Критерий завершения вычислений имеет вид: | x_n+1 - x_n | £ 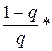e,

где q = max|j' (x) |, при x 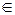[ a,b ] и e - заданная точность.

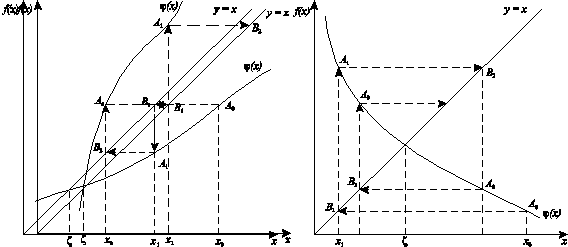
На рис. 4.3 приведена геометрическая интерпретация сходящегося (|j' (x) |< 1)и расходящегося (|j' (x) | > 1)итерационных процессов.