1. Решить задачу Коши для дифференциального уравнения первого порядка:
- методом численного интегрирования,
- методом Эйлера (модифицированным),
- методом Рунге-Кутта второго и четвертого порядка точности,
- методом Адамса,
- методом Милна.
2. Сравнить полученные результаты с точным решением.
Варианты
1. 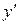 = ex y 2-2 y; y(0)=1/2; xÎ[0;2]; h=0,1; y т=
= ex y 2-2 y; y(0)=1/2; xÎ[0;2]; h=0,1; y т= 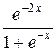 .
.
2. 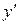 =ex - е-x; y(0)=0; xÎ[0;1]; h=0,1; y т=
=ex - е-x; y(0)=0; xÎ[0;1]; h=0,1; y т= 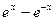 .
.
3. 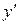 =x
=x 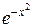 - 2 x y; y(0)=0; xÎ[0;1]; h=0,1; y т=
- 2 x y; y(0)=0; xÎ[0;1]; h=0,1; y т= 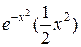 .
.
4. 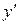 =sin (2 x) – y tg(x); y(0)=0; xÎ[0;p]; h=0,1; y т =-2cos2 x+2cos x.
=sin (2 x) – y tg(x); y(0)=0; xÎ[0;p]; h=0,1; y т =-2cos2 x+2cos x.
5. 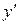 =x y2+y; y(0)=1; xÎ[0;1]; h=0,1; y т =
=x y2+y; y(0)=1; xÎ[0;1]; h=0,1; y т = 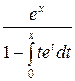 .
.
6. 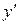 =ex-y - ex; y(0)=ln(2); xÎ[0;1]; h=0,1; y т =ln[1+2,7182818exp(-ex)].
=ex-y - ex; y(0)=ln(2); xÎ[0;1]; h=0,1; y т =ln[1+2,7182818exp(-ex)].
7. x 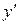 +y=x sin (x); y (
+y=x sin (x); y (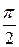 )=
)= 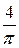 ; x Î[
; x Î[ 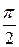 ; p ]; h =0,1
; p ]; h =0,1 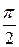 ; y т=
; y т= 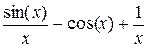 .
.
8. x 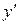 -y=x2 sin (x); y (
-y=x2 sin (x); y (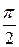 )=1; x Î[
)=1; x Î[ 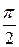 ; p ]; h =0,1
; p ]; h =0,1 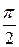 ; y т= x(
; y т= x(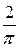 - cos (x)).
- cos (x)).
9. x 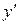 - y2+1=0; y (0,1)=0; x Î[0,1;1]; h =0,1; y т=
- y2+1=0; y (0,1)=0; x Î[0,1;1]; h =0,1; y т= 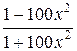 .
.
 2015-07-14
2015-07-14 341
341








