Пусть дана сложная функция  , то есть такая, что ее можно представить в виде:
, то есть такая, что ее можно представить в виде: 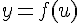 , при этом
, при этом 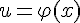 . Переменную
. Переменную 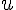 также называют промежуточным аргументом. Следующая теорема определяет правило дифференцирования сложной функции.
также называют промежуточным аргументом. Следующая теорема определяет правило дифференцирования сложной функции.
Теорема. Если функция 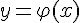 имеет в некоторой точке
имеет в некоторой точке 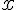 производную
производную 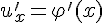 ,а функция
,а функция 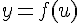 имеет при соответствующем значении
имеет при соответствующем значении 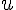 производную
производную 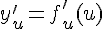 , то сложная функция
, то сложная функция 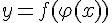 в указанной точке
в указанной точке 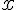 имеет производную, которая равна
имеет производную, которая равна 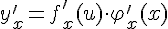 , где вместо
, где вместо 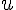 должно быть подставлено выражение
должно быть подставлено выражение 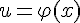 .
.
Коротко это правило записывается так: 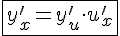 , то есть производная сложной функции равна произведению производной данной функции по промежуточному аргументу
, то есть производная сложной функции равна произведению производной данной функции по промежуточному аргументу 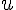 на производную промежуточного аргумента по
на производную промежуточного аргумента по 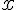 .
.
На практике чаще всего приходится находить производные от сложных функций. Поэтому ниже приводится таблица производных для сложных функций, в которой аргумент 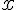 заменен на промежуточный аргумент
заменен на промежуточный аргумент 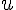 .
.
1. 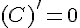
2. 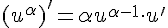
3. 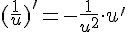
4. 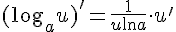
5. 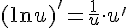
6. 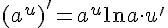
7. 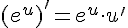
8. 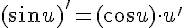
9. 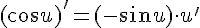
10. 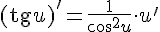
11. 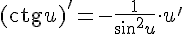
12. 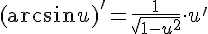
13. 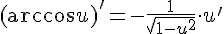
14. 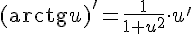
15. 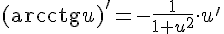
16. 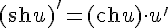
17. 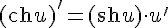
Пример. Вычислить производную функции 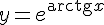 .
.
 2015-07-14
2015-07-14 903
903








